Data Management Probability Formulas

These flashcards focus on key concepts and formulas related to Data Management and Probability, including unions, intersections, and various probability formulas.

Union (AUB)

All outcomes in A, B, or both.

Intersection (A∩B)

Only outcomes in both A and B.

Counting formula for two sets

n(AUB) = n(A) + n(B) - n(A∩B), finds the # of ways A or B happens

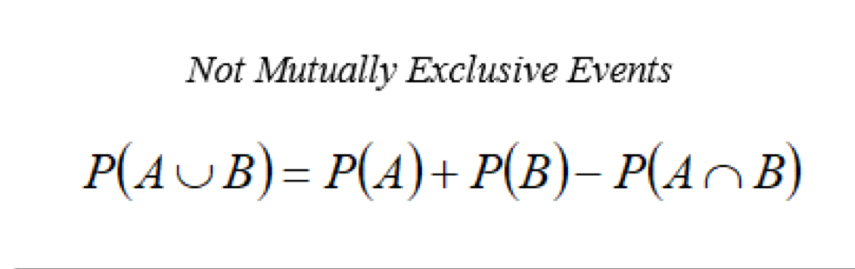
Counting formula for three sets

n(AUBUC) = n(A) + n(B) + n(C) - n(A∩B) - n(A∩C) - n(B∩C) + n(A∩B∩C), finds the # of ways A, B, or C happens

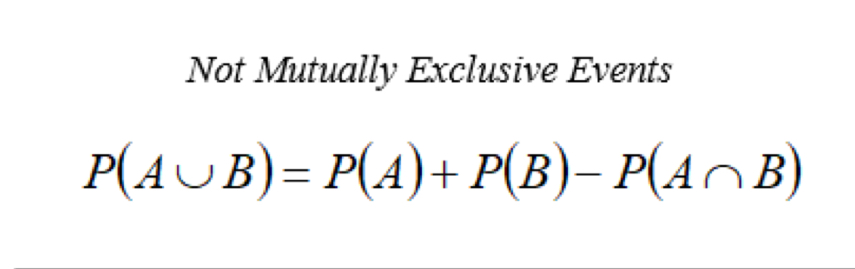
Mutually exclusive formula

P(AUB) = P(A) + P(B), probability either A or B happens / chance of at least one occurring

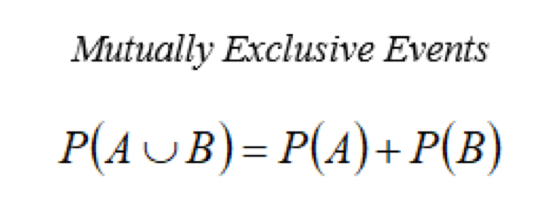
Independent events formula

P(A∩B) = P(A) · P(B), finds probability that A and B happens at the same time given the events don't effect each other.

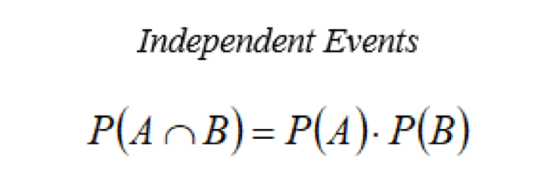
Conditional probability

P(A|B) = P(A∩B) / P(B), the probability of A given B.

Baye's formula

P(Aₖ | E) = P( E | Aₖ) * P(Aₖ)) / Σi=1 P(Aᵢ) P(E | Aᵢ), to find the probability of Aₖ happening out of several events given event E happened

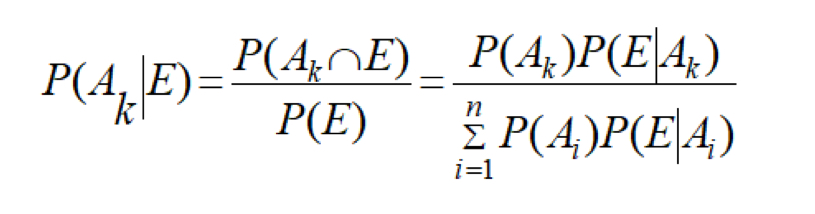
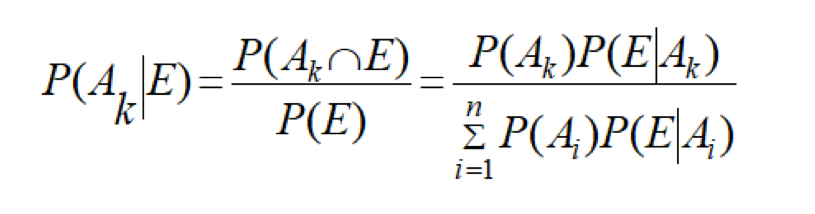
Explain Baye’s Formula individual parts: i, k, P(Aₖ), P(E|Aₖ), Σi=1 P(Aᵢ) P(E | Aᵢ)

P(Aₖ | E) = P( E | Aₖ) * P(Aₖ)) / Σi=1 P(Aᵢ) P(E | Aᵢ)

k: the cause you’re focused on

i: all possible causes

P( E | Aₖ) : how likely E is given Aₖ happened

Σi=1 P(Aᵢ) P(E | Aᵢ) : total probability of E accounting for all causes

Odds in favour formula

P(A) / P(A’) = P(A) / (1 - P(A)) = success / failed

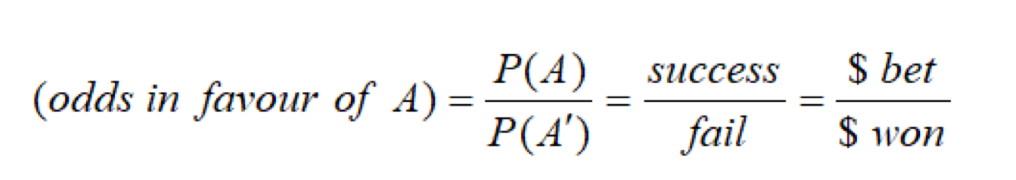
Odds against formula

P(A’)/P(A) = 1-P(A)/P(A) = failed / success

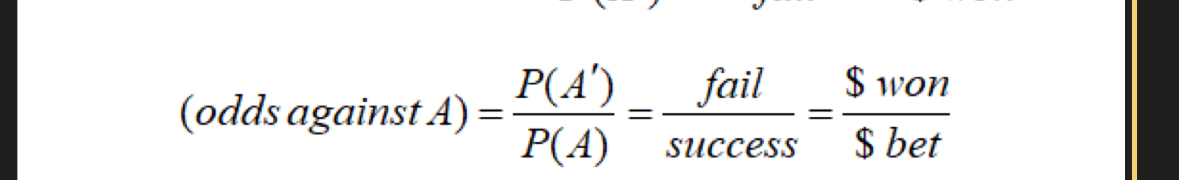
Odds in favour (money) formula

Money wagered / money won

Probability formula

Success / total

Birthday problem

P(repeat) = 1 - [ nPr / n^r]

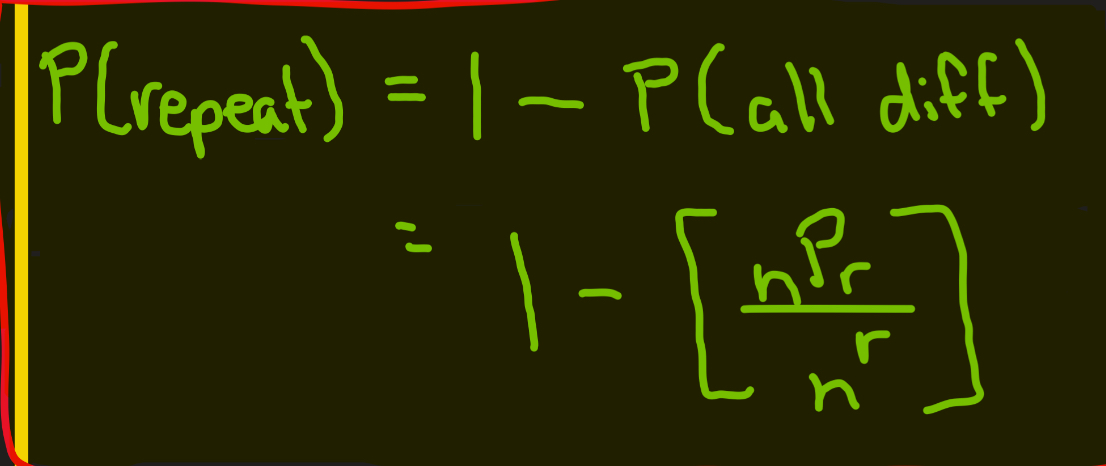
What each component of the birthday problem means: n, r, nPr, and n^r, all together

n - # of options for each choice

r - # of slots you are filling

nPr - # of ways to choose r things from n without repeats and with order mattering

n^r - total # outcomes with repeats

All together - # of ways to assign unique values to r slots, divided by the total number of all possible assignments, including repeats to find probability that no two selections are the same