Lecture 9: Factorial Design, Correlational Research

CHAPTERS 11 AND 12

Factor

• 2 or more independent variables are combined in an experiment

• each factor can have multiple levels each leading to multiple combinations

Factorial Design

• a research design that includes 2 or more factors

• described by how many factors it has, two-factor design, three-factor design etc

• the levels of one factor determine the columns and the levels of the second factor determines the rows

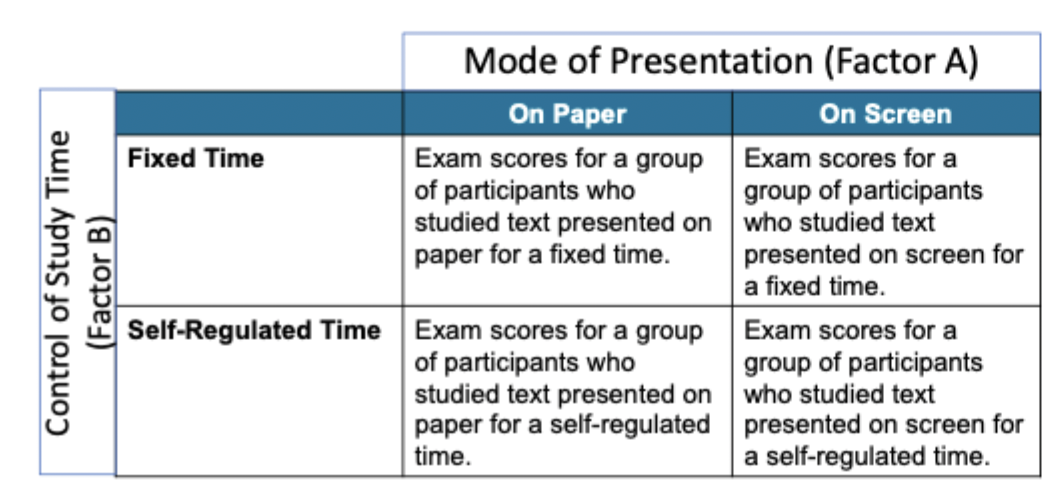
Main Effects

• The individual impact of each factor on the dependent variable in a factorial design, without considering interactions between factors.

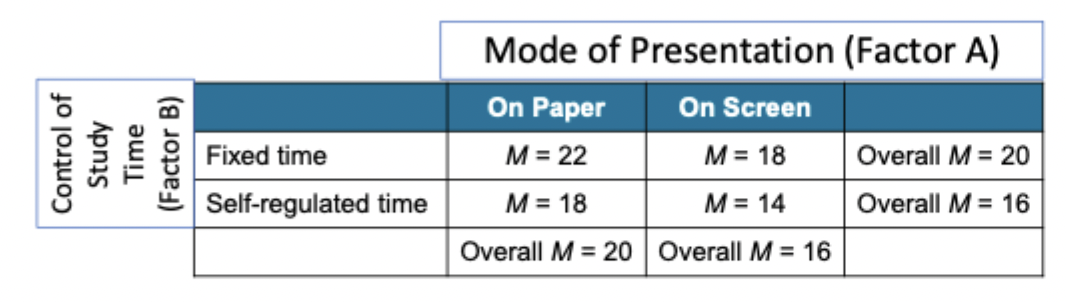
• The mean differences among the columns or rows determine the main effect for one factor

  • 2-factor study has 2 main effects; one for each factor

  • statistical test needed to see if differences are signicant

Interaction Between Factors

• One factor has a direct influence on the effect of a second factor

• e.g Drug interaction: one drug modifying the effect of another drug

  • One drug can exaggerate the effects of another

  • one drug may minimize or completely block the effects of another

• When factors are independent, they have no interaction

• presence of a second variable shows if something was done

Describing an interaction between factors

• When the effects of one factor depend on the different levels of a second factor

or

• When the results of a two-factor study are graphed

  • nonparallel lines = an interaction (when they meet something happens)

  • A statistical test is needed to determine if the interaction is significant

Identifying an interaction in a data matrix

• compare the mean differences in any individual row with the mean differences in other rows (works with columns too)

• The size and the direction of the differences in one row are the same as the corresponding differences in other rows in the matrix = no interaction

• Differences change from one row to another in the matrix = evidence of an interaction

Interpreting Main Effects and Interactions

• Significant effects indicated by a statistical analysis

  • have to be careful about interpreting the outcome

• Main effects may present a distorted view of the actual outcome

• Each main effect is an average

  • it may not accurately represent any of the individual effects that were used to compute the average

Interpreting Main Effects and Interactions (2)

• The two-factor study allows researchers to evaluate three separate sets of mean differences

  • Main differences from the main effect of factor A

  • Main differences from the main effect of factor B

  • Main differences from the interaction between factors

Types of Factorial Designs

• Between-Subjects

• Within-Subjects

• Mixed Design: Within and Between subjects

• Experimental

• Non-experimental or Quasi-experimental

Between-Subjects

• Requires a large number of participants → Disadvantage

• separate group of participants for each of the treatment conditions

• Individual Differences can become confounding variables → disadvantage

• Avoids order effects, each score is independent → Advantage

Within-Subjects

• A single group of individuals participates in all of the separate treatment conditions

  • 2 × 4 study = everyone does 8 treatment conditions

• each participant must undergo a high number of treatments → Disadvantage

  • Time-consuming and contributed to participants dropping out of the study (attrition)

• Testing effects - fatigue or practicing before the next treatment → disadvantage

• Eliminates problems with individual differences

Mixed Design: Within and Between-Subjects

• a factorial study that combines two different research designs

• a factorial study with one between-subjects factor and one within-subjects factor

Experimental

• a factorial study that is a purely experimental research design

• Both factors are true independent variables that are manipulated by the researcher

Non Experimental or Quasi-Experimental

• a factorial study for which all the factors are nonmanipulated, quasi-independent variables

• The nonmanipulated variables are still called factors

Quasi-Independent Variable

• the variable is used to differentiate the groups of participants or the groups of scores being compared

• preexisting factors

Dependent Variable

• The variable that is measured to obtain the scores within each group

Combined Strategies

• Uses two different research strategies in the same factorial design

• One factor is a true IV (experimental strategy where they manipulate)

• the second factor is a quasi-independent variable (exists already/no manipulation)

  • Nonexperimental or quasi-experimental strategy

  • falls into one of the following categories: a preexisting participant characteristic or (gender/age or time (how long things persist)

Statistical Analysis of Factorial Design

• Depends partly on whether the factors are between, within, some mixture of both

• The standard practice includes

  • Computing the mean for each treatment condition (cell)

  • Using ANOVA to evaluate the statistical significance of the mean differences → Use three tests for all main differences

Goals of the Correlational Research Strategy

• two or more variables are measured to obtain a set of scores (usually two scores) for each individual

• to establish that a relationship exists between variables

• to describe the nature of the relationship

  • the relationships can be described not explained

  • there is no attempt to manipulate, control or interfere with the variables

Comparing Correlational and Experimental

• Correlational Research → intended to demonstrate the existence of a relationship between 2 variables

  • does not determine cause and effect relationship (no explanation)

  • looks for patterns within the scores of individuals

• Experimental Research → demonstrates a cause-and-effect relationship between two variables

  • can manipulate one variable to create treatment conditions

  • measure the second variable to obtain a set of scores for each condition

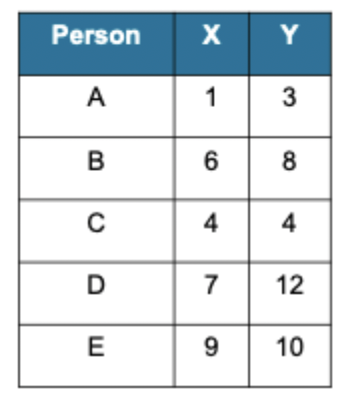
Data and Statistical Analysis: Chart

• Scores in each pair are identified as X and Y

• Data can be presented in a list showing the two scores for each individual

• like a tally chart

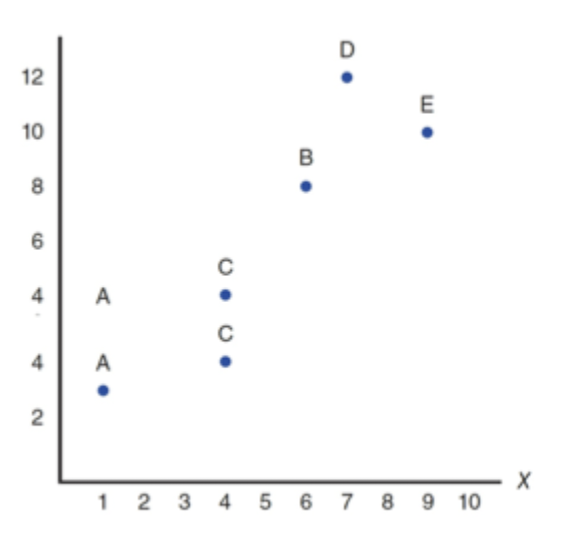
Data and Statistical Analysis: Scatter plot Graph

• scored can be shown in a scatter plot graph

• Each individual score is shown as a single dot w/ a horizontal coordinate x and a vertical coordinate y

• benefits: allows you to see the characteristics of the relationship between the two variable

Three characteristics of a relationship when measuring are…

• direction

• form

• consistency of strength

• measures and describes the relationship between two variable

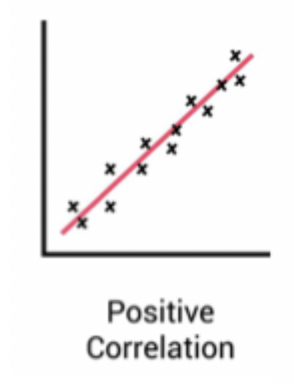
Direction of Relationship: Positive Relationship

• Two variables change in the same direction

• as one variable increases → the other variable increases

• greater than 0

• slope up the right

• e.g height and weight - the taller students tend to weigh more

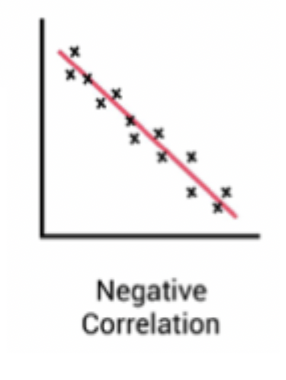
Direction of Relationship: Negative Relationship

• Two variables change in opposite directions

• Increases in one variable → matches with decreases in the other variable

• e.g performance tasks - the faster you are, the lower the accuracy

• less than zero

• sloped down to the right

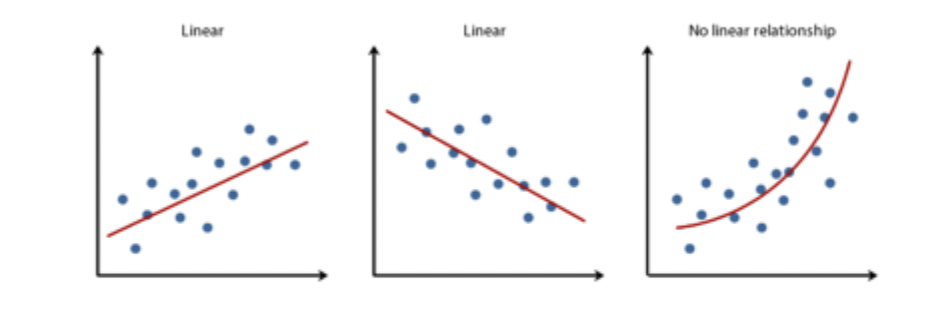
form of Relationship: Linear Relationship

• The data points in the scatter plot tend to cluster in a straight line

• Positive Linear Relationship

  • Each time the x variable increases, the Y variable increases/decreases in a consistently predictable amount

  • A Pearson correlation describes and measures linear relationships when both variables are numerical scores from interval or ratio scales

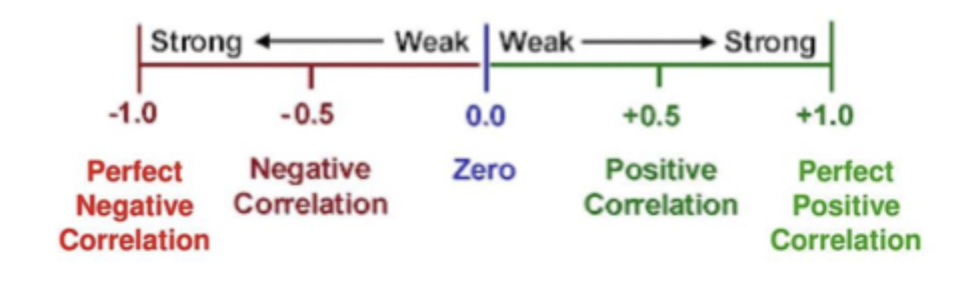
Consistency of strength of relationship

• Correlation (correlation coefficient): measures and describes the relationship btwn 2 variables

  • The sign (+/-) indicates the direction of the relationship

  • The numerical value (0.0-1.0) indicates the strength or consistency of the relationship

Interpreting the Strength of a Correlation

• Coefficient of determination: The squared value of a correlation (r²⁾

  • measuring the strength

• Measures the percentage of variability in one variable that is determined, or predicted, by its relationship with the other variable

• the value of the correlation that goes from 0.00 (lack of consistency) to 1.00 (perfectly consistent relationship)

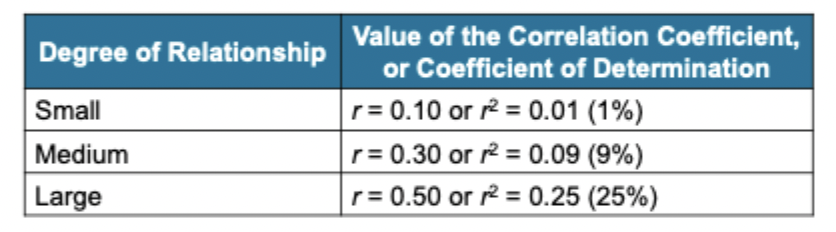
Statistical SIgnificance of a Correlation

• The correlation is unlikely to have been produced by random variation

• when the sample correlation is found to be significant, you can reasonably conclude that it represents a real relationship that exists in the population

• With a small sample, it is possible to obtain what appears to be a very strong correlation when, in fact, there is no relationship between the two variables

• Increasing the sample size makes it more likely that a correlation represents a real relationship

  • does not mean it is large or strong

Applications of the Correlational Strategy: Prediciton

• a correlational study demonstrating a relationship between two variables

• Allows researchers to use knowledge about one variable to help predict or explain the second variable

• e.g relationship between good SAT scores and future grade point average in college, help college administrators to predict who is most likely to be successful

• not just predictions of the future, one variable can predict the other

Reliability and Validity and Explaining theories

• Both reliability (consistency and stability of measurements) and validity (extent to which procedures actually measure what it claims to)

  • commonly defined by relationships that are established using the correlational research design

  • e.g if the same individual is measured twice under the same conditions, there is a consistent relationship between the 2 measurements (reliability) and get the same results from previous tests (validity)

• Correlational research can be used to address many theoretical questions

  • e.g Studies of IQs of identical twins

Strengths of Correlational Research

• Describes the relationship between variables

• Nonintrusive (natural behaviours)

• High External Validity

Weaknesses of Correlational Research

• Cannot assess causality

• third-variable problem

• Directionality problem

• Low internal validity

Directionality Problem

• Weakness

• A correlational study does not establish a relationship of cause-and-effect

• correlational cant determine which variable is the cause and which is the effect

The Third-Variable Problem

• b/c two variables are related, does not mean that there must be a direct relationship between the two variables

• A third (unidentified) variable may be responsible for producing the observed relation