CISC 251 Quiz 2

data, model, predictions, output features, input features, relationships

Machine learning algorithms use ______ to build a ______ that makes _______________.

Machine learning algorithms make predictions about ___________ based on values of _____________, or uncover ________________ between features.

model training

______________ is the process of estimating model parameters used to make a prediction

Ex. When predicting car insurance premiums using incurred losses, the slope and intercept parameters of a linear regression model are estimated during model training 

sample data, training data, validation data, test data

Model Training:

1. Training data is obtained from _____________

2. A machine learning algorithm fits a model or several models using _____________

3. Often, data analysts use _______________ to optimize the performance of models.

4. ____________ is used to see how well models perform when predicting unseen data.

training data

_____________ is used to fit a model

validation data

_______________ is used to evaluate model performance, adjust parameters or model settings, and conduct feature selection

test data

____________ is used to evaluate final model performance and compare different models

similar

Data distribution between training data, validation data, and test data should be ____________ or else the model will not perform well

60-90%

Usually ________ of the data is chosen as training data, with the remaining data split between validation and test.

metric

A ________ is a numeric value that evaluates how closely a model fits the sample data

mean squared error, low

________________ or MSE measures the average squared difference between predicted and actual values, capturing both the variance of the errors and the squared bias

Models with accurate predictions will have _______ MSE

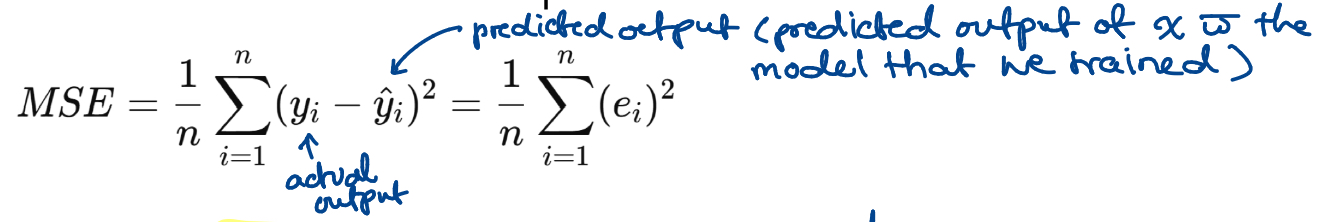
prediction error, residuals

The ______________ of an instance i is the difference between the observed value, y_i, and the predicted value y-hat_i

Also called ________ and denoted e_i = y_i - y-hat_i

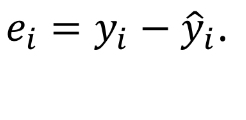
bias, variance, irreducible error

Over many possible training datasets, the total expected prediction error of a model can be broken into three parts…

bias

________ is the error that is introduced by approximating a real-life problem, which may be extremely complicated, by a much simpler model

variance

__________ is how much the model’s predictions vary across different training datasets

irreducible error

____________ is the inherent randomness in the data, determined by the process, not the model

expected prediction error of a model

The ________________________ at a particular data point, x, can be expressed as… [see image]

bias

_______ is the difference between the average prediction of our model and the true value we are trying to predict

high bias, underfitting

A ___________ means the model is making systematic errors and is likely too simple to capture the underlying patterns in the data. 

This is also known as ________________

model fitting, model assumptions, systematic errors

Bias is caused by:

• Poor _____________ or violating _______________

• Underlying ______________ in the data, such as underrepresenting a particular group or failing to measure an important feature

prediction variance

______________ measures how much the model’s predictions would change if we were to train it on a different training dataset

high variance, overfitting

_____________ indicates that the model is very sensitive to the specific training data it was given, and it may be capturing random noise instead of the underlying signal.

This is also known as ______________

low bias, low prediction variance

Models with _________ and ______________ have predicted values that are consistently close to the observed values even across different datasets

bias, variance, bias, variance, bias, variance, total error

Increasing model complexity usually reduces ______ but increases ___________.

Simpler models usually increase _______ but reduce __________.

Goal is to find a balance where both ______ and _________ are low enough to minimize the ____________.

low, high, high, low, high, high

A model with _____ bias and _____ variance occasionally hits the bullseye but is less consistent.

A model with _______ bias and ______ variance consistently hits the same spot on the target, just not the center.

The worst-case scenario is a model with _____ bias and _____ variance because they are inaccurate and inconsistent.

form/complexity

Choosing the ____________ of a model is a key step in model building

underfit

A model is ________ if the model is too simple to fit the data well. 

These models tend to miss the underlying trend and score poorly in metrics.

overfit

A model is ________ if the model is too complicated and fits the data too closely. 

These models do not generalize well to new data and will miss the general trend of the data despite scoring well in metrics.

optimal

An __________ model is complicated enough to describe the general trend in the data without incorporating too much variation

K-nearest neighbours

_______________ is a supervised classification algorithm that predicts the class of an output feature based on the class of other instances with the most similar, or “nearest,” input features

regression

K-nearest neighbours (KNN) is used to predict numerical values, so it works best with ___________ models

Euclidean distance

In KNN, the most common distance metric is the __________________ [see image]

weighted KNN, K, randomly

Ways to break a tie in KNN:

1. Apply _____________ (give more weight to closest points)

2. Change ___

3. ___________ pick one of the values (easiest)

decision boundary

The ______________ of a classification model is the edge or edges separating the classes

scatter plot, potential predictions, parameter values

Decision boundaries are plotted on a ______________, with the background shading corresponding to the classification in a particular region.

Decision boundary plots help data analysts explore _______________ from a supervised learning model and explore how models change depending on ________________, such as k.

metric

In KNN, a _________ is a method for determining the distance between two instances

euclidean distance, manhattan distance, minkowski distance, cosine similarity (similarity)

In KNN, the four different distance metrics are…

cosine similarity, same, cosine, -1, 1

Type of KNN distance metric (similarity) ______________:

• Used for checking if vectors are pointing in the ______ direction

• Measures the _______ of the angle between two vectors in a multi-dimensional space

• Used for comparing the similarity between document vectors, text data, and high-dimensional data

• Values range from ___ (completely dissimilar) to ___ (identical or similar in direction)

euclidean distance, continuous numerical, low-to-moderate

Type of distance metric for KNN ________________:

• The most common choice for _________________ data in _________________ dimensions. It assumes features are on comparable scales (so scaling/normalization is important)

manhattan distance, high dimensional, sparse, categorical-like, counts, scaling

Type of distance metric in KNN _________________:

• Often better in ________________ spaces because it reduces the effect of very large differences in individual features

• It’s also useful for ________ or ______________ data encoded as _________

• _______ is also important

cosine similarity, clustering, orientation (angle), magnitude

Type of distance metric for KNN ________________:

• Widely used in text mining, natural language processing (NLP), recommendation systems, and __________ high-dimensional sparse vectors, since it focuses on ________________ rather than _____________

distance-based algorithms

____________________, such as KNN, make predictions based only on the most similar instances, and do not consider relationships between input and output features

unit, magnitude, measurement

K-nearest neighbours (KNN) is sensitive to the ______ and __________ of _______________ for each feature

input, standardized

________ features in distance-based algorithms should be ____________ before fitting a model

standardized features, 0, 1

_________________ are scaled to have a mean of ___ and a standard deviation of ___

mean, standard deviation

A feature is standardized by subtracting the ________ and dividing by the ________________

z-scores

Standardized values are also referred to as __________

elbow method

The ____________ is a method for choosing K in KNN where you try multiple Ks and graph the error rate; then, pick the one with the lowest rate

1, single, training set, class, high, noise, outliers, generalization, overfits

In KNN, if K = ___:

• The KNN model considers only the ________ nearest neighbour when making predictions.

• The model essentially memorizes the __________; it predicts the _______ of the closest point.

• This leads to _____ variance: the model is very sensitive to _______ and _________.

• It lacks ______________ and doesn’t capture broader patterns or relationships in the data (_________).

N, neighbours, majority, mode, similarity, bias, common, underfits

In KNN, if K = ___:

• The KNN data considers all data points as ___________.

• Every query point is classified by the __________ class of the entire dataset (the _____).

• This ignores actual __________, since even very distant points influence the prediction.

• The model becomes too rigid (high _____) and loses the ability to capture meaningful patterns.

• In practice, predictions collapse to always predicting the most _________ class (_________).

majority class

In KNN, prediction is based on the ____________ among the K nearest data points

weighted, weight, distance, nearby, farther away, closer

_________ KNN is similar to KNN, but the nearest k points are assigned a _______ based on their __________.

More weight is given to the points which are _______ and less weight is given to the points which are ______________, so _________ neighbours have a stronger influence on the prediction.

hyperparameter

A ________________ is a user-defined setting in a machine learning model that is not estimated during model fitting

log-odds, negative infinity, positive infinity, 0, 1

The __________ is the natural log, ln(.), of the ratio of the probability that y_i = 1 to the probability that y_i = 0. 

Ranges from ___ to ___, unlike p_i, which is bounded between ___ and ____.

logistic regression, linear, binary

______________ is a classification model which uses a _______ function to predict the log-odds of a given outcome. 

Most often ________, but can be extended to multiclass.

sigmoid, S

A logistic regression model uses the _________ (logistic) function, which produces an ___-shaped curve when plotting predicted probabilities against the input

nonlinear, predictors, predicted probability, linear, log-odds

Logistic regression produces a __________ relationship between the __________ and the _________________, but the model is _______ in the parameters with respect to the ________

probability, threshold, 0.5

Logistic regression returns a predicted ____________ of class membership. To turn this into a class prediction, we usually apply a ___________:

• Ex. If p >= T, predict class 1. Else p < T, predict class 0. 

For a binary classification problem, the most common threshold is _____.

model-based, weights

Logistic regression is a ___________ algorithm; the logistic regression ________ directly describe the relationship between the inputs and outputs

one-vs-rest, single multinomial, softmax

When more than two classes exist, logistic regression can be extended either by training multiple ___________ models (one per class) or by fitting a _______________ logistic regression model using the ________ function

maximum likelihood estimation, 1, 1, 0, 0, maximized

Logistic regression is fit using __________________ or MLE.

The idea is to find coefficients B_0 and B_1 such that the predicted probabilities are close to ____ for individuals in class ____ and close to ____ for individuals in class ____.

This is formalized by a likelihood function, which is ___________ to obtain the estimates.

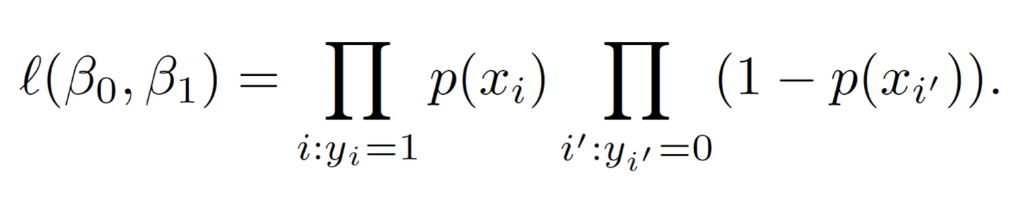
conditional probability

____________________ measures the probability that an event occurs, given another event has also occurred

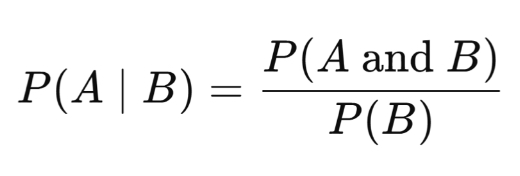
bayes rule

Type of probability rule

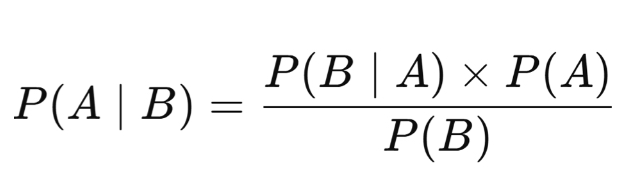
bayes rule

You can get all the components needed for the ____________ formula if you have access to the original dataset

naive bayes classifier, prior probability, posterior probability, likelihood, evidence

__________________ uses Bayes’ rule to classify instances based on conditional probabilities:

• The _______________, P(y_i), represents the overall probability of class y_i

• The __________________, P(y_i|x), represents the probability of class y_i, given certain values of the input features x

• The ____________, P(x|y_i), tells us how probable it is to see the features x given that the instance belongs to class y_i

• The ____________, P(x), is the total probability of observing features x, across all classes

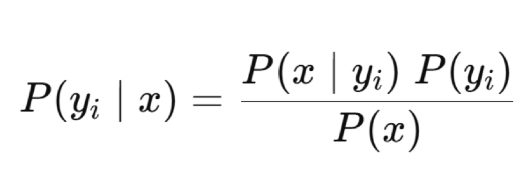
independent, uncorrelated, equally, rarely

Naive Bayes assumptions:

• All input features are _____________ or ______________

• All input features are _________ important

In reality, the Naive Bayes assumptions are ________ satisfied

input feature, input features

The naive Bayes assumptions are always met for a single _____________ since no relationship to other _____________ can exist

continuous probability distribution

A ___________________ is a mathematical function that describes the probability that a certain value of a random variable occurs

normal distribution

The ________________ is a symmetric, bell-shaped distribution with two parameters: the mean and the standard deviation

gaussian naive bayes

________________ uses the normal distribution as an approximation to the conditional probability P(x|y_i)

center

The mean sets the ________ of a curve

spread

The standard deviation sets the ________ of a curve

naive bayes classifiers

Bayesian models, including ______________________, incorporate prior assumptions about the probability that a given event occurs in the model’s prediction. 

sample, prior, prior, priors, priors, posteriors

By default, most implementations of naive Bayes classification use the _________ probabilities of each class as the _______ probabilities. 

Adjusting the _______ probabilities may have an impact on the model’s predictions and performance (be careful about this!)

AKA:

_______ are calculated based on the training dataset.

If _____ change, then the _________ calculated will not be accurate.

fast, unrealistic, violated

Naive Bayes pros and cons:

• Nave Bayes’ predictions are _____ to compute, since predictions are based on conditional probabilities. 

• But the naive Bayes assumptions are often ___________.

• If the predictions are fast and accurate, naive Bayes may still be useful despite __________ assumptions.

discriminant function, unique, predicted

A _________________ is a function used to set a decision boundary between classes. 

This function is _______ in each class, and the class with the highest value of this function for a given set of input values is the ___________ class.

normality, equal covariance, independence

The main assumptions in linear discriminant analysis:

• ___________: Each class’s features are assumed to follow a multivariate normal distribution

• _______________: Each class shares the same covariance matrix. This is what makes the decision boundaries linear.

• _______________: The observations are independent of each other.

covariance

____________ measures how values of one feature change in relation to a second feature

covariance matrix

A __________________ is a matrix containing all pairwise covariances between features i and j, denoted Σ

any, linear decision boundary, quadratic discriminant analysis, curved decision boundary, complex, less

Linear Discriminant Analysis (LDA) pros and cons:

• Linear discriminant analysis extends to _____ number of classes

• But, restricting the discriminant functions to linear equations results in a ________________________

• _____________________ uses quadratic equations in the discriminant functions

• The resulting discriminant equations are more complicated, but in some situations, a ____________________ is a better fit

• A tradeoff exists between model complexity and interpretability: more __________ models are _____ interpretable

covariance matrix

In quadratic discriminant analysis (QDA), each class has its own __________________

simple linear regression

____________________ models predict the output feature based on a linear relationship with only one input feature

residual

In simple linear regression, one measure of closeness is the _________, which is the vertical distance between the i^th observed data value and the predicted value for the i^th instance by the linear model

least squares

In simple linear regression, _____________ selects weights such that the sum of the squared residuals is minimized

linear, additive, independent, normally distributed, constant variance, inaccurate

Linear regression assumptions:

• The relationship between output feature and the input features is _________ and ___________

• The residuals are ____________, ______________, and have a ______________ across the range of x values

• The impact of an assumption not being reasonably met is dependent on the assumption

  • Ex. If the relationship between the output feature and the input features is not linear, the model’s estimated weights, and thus predictions made with the model, will be ____________

linear, reasonably, efficient, straightforward, outliers, multicollinearity, noise, overfitting

Linear Regression pros and cons:

• Linear regression methods perform well when the relationship between the output and the input features is _________ and assumptions are _____________ met

• Linear regression models are also computationally ___________ and _____________ to interpret

• Linear regression methods are sensitive to ________ and extreme instances, sensitive to ______________, which occurs when input features are correlated, and susceptible to ________ and ___________

inference, linear regression, KNN

In a real system, ___________ is how long it takes to produce an outcome

• Very low for ______________, very high for _____

K-nearest neighbours regression, distance, average

_______________________ predicts the value of a numeric output feature based on the average output for other instances with the most similar, or nearest, input features

• Identified using a _____________ measure with the input features

• The _________ value of the output feature for the nearest instances becomes the prediction

value of k, distance measure

KNN regression has two main hyperparameters: the __________ and the __________________

overfitting, underfitting, k

In KNN regression, setting k too small may result in ____________ and setting k too large may result in ______________

• KNN regression predictions are based on the output feature of the ____ closest instances

complex, nonlinear, noise, outliers, input features, instances, high, expensive, large, scale

KNN Regression pros and cons:

• Since KNN regression does not require a specific relationship between the input and output features, the model works well for ________ or __________ relationships

• For a large enough k, the model is not sensitive to _______ or ___________

• The KNN algorithm is sensitive to the number of ____________ and the number of __________:

  • When the number of input features becomes _______, the nearest neighbours for a new instance may not be similar and result in poor predictions

  • Because the KNN regression algorithm calculates the distance between x and each instance, the algorithm is computationally ___________ for datasets with a _______ number of instances

• Practical note: _______ features before KNN (otherwise one feature’s units dominate the distance)

experience (data), task (goal), model (hypothesis), loss function (objective), evaluation (metrics)

The machine learning components are…

experience (data)

A machine learning component:

• What the model learns from

task (goal)

A machine learning component:

• What the model aims to achieve

model (hypothesis)

A machine learning component:

• How the task is performed

loss function (objective)

A machine learning component:

• Measures training performance

evaluation (metrics)

A machine learning component:

• Measures generalization

loss function

A _____________ for regression measures how close a model’s predictions are to the actual values

weights, minimize

Regression models are fitted by selecting ______ that _________ the specified loss function

absolute loss, squared loss, Huber loss, quantile loss

Common loss functions for regression include…

predict, loss, weights, high, change, low, keep, repeat

Basic idea of training a regression model:

1. ________:

   • Use the current weights to compute predictions

2. Compute _______:

   1. Measure how wrong the predictions are

3. Adjust _________:

   1. If the loss is ______, it means predictions are poor → ________ the weights (move them in the direction that reduces loss)

   2. If the loss is _______, it means predictions are good → ______ the weights (or change very little)

4. _______ until the loss stops decreasing (i.e. the model has “converged”)