Week 1 Lecture 1 - Strings, grammars and finite state automata

What are the 3 central concepts?

Language

Grammar → A set of rules that specify the language

Automaton → An abstract computational machine that recognises members of the language [plural: Automata]

What does ‘Σ’ represent in automata theory?

Alphabet → Finite nonempty sets of symbols.

Σ = {0,1} or = {a,b,c,…}

Σ is a set of ASCII characters

What is a string in automata theory?

Sequence of symbols of the alphabet including the
empty string, λ

Σ^k set of strings of length k.
– Σ^* union of all strings of length k ≥ 0.
– Σ^* = Σ₀ ∪ Σ₁ ∪ Σ₂ ∪ ⋯, where Σ₀ = {𝜆}.
– We can define the set that excludes the empty string :
Σ⁺ = Σ₁ ∪ Σ₂ ∪ ⋯

What are languages in automata theory?

Sets of strings chosen from some Σ^*

L is a language over Σ: L ⊆ Σ^*

It is just a set of strings.

Concatenation of languages L₁ and L₂

L₁L₂ is defined by:

{𝑥𝑦 𝑥 ∈ 𝐿₁ ∧ 𝑦 ∈ 𝐿₂}

The set of all strings not in L:

L (with a line on top) = Σ^* − 𝐿

Assume 𝑎, 𝑏 and 𝑎𝑖, 𝑏𝑖 are members of Σ

What are:
𝑎ⁿ

𝑤 = 𝑎₁𝑎₂ … 𝑎_n and 𝑣 = 𝑏₁𝑏₂ … 𝑏_m

|𝑤|

→ a…a

→ 𝑎₁𝑎₂ … 𝑎_n𝑏₁𝑏₂ … 𝑏_m

→ The length of 𝑤

What does a transition graph consist of?

→ States

→ One initial state

→ One or more final/accepting states

→ Labelled transitions between states

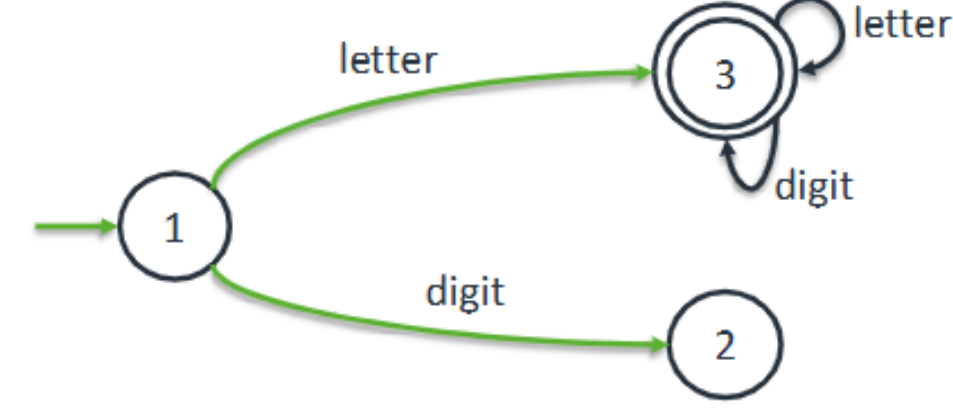
For this transition graph, give the lexical analyser:

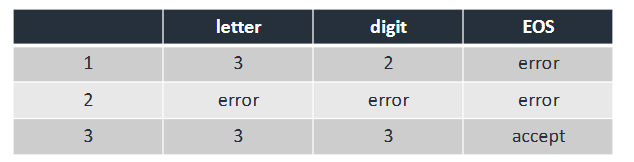
For this transition graph, give the transition table:

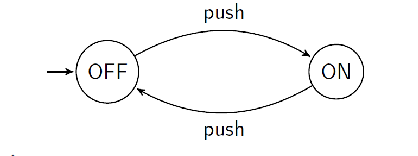
For this off-on switch, prove using induction:

𝑆₁(𝑛): automaton is off after n pushes iff n is even

Base: n = 0

OFF is initial state, therefore when n = 0 the state is off. Therefore n is even.
𝑆₁(0) = (𝑡𝑟𝑢𝑒 ⇔ 𝑡𝑟𝑢𝑒)

Inductive:

𝑆₁(𝑛 + 1)
Automaton is off ⇒ 𝑛 + 1 is even
Assume automation is off when n + 1 pushes
n is not even, by S₁(n)
n is odd
n+1 is even