lecture 5- experimental design

How can an experiment support causal claims?

• if we observe a change in the DV after ONLY the IV was changed, the change must be due to the change in IV

What are confounding variables?

An extraneous variable (not being investigated) that varies systematically with the IV and can explain changes in the DV.

Examples:

• ppt characteristics

• Situational variables e.g. time of day, environment

What are experimenter expectancy effects?

• a special type of confounding variable that varies with IV and explains differences in DV

• Occurs when an experimenter’s expectations about how ppts should behave in experiment affects how they behave.

What is the subject expectancy effect?

• confounding variable

• Occurs when ppts’ knowledge or assumptions about hypothesis influences their behaviour

How do you deal with confounding variables?

• keep ppt characteristics between groups the same

• Keep situational characteristics the same

• Keep ppt and experimenter expectations the same

• Standardise procedure

• Blinding

• Random allocation design

What is standardisation?

Keeping research procedures identical for all ppts.

• standardisation of study environment

• Standardisation of instructions

• Standardisation of stimulus material in each condition

What is blinding?

Blinding protects against subject and experimenter expectancy effects.

• double-blind study = neither experimenters nor ppts know what group they are allocated to

• Single-blind study = only ppts are naive to condition they are in

What is random allocation design?

• ppts are randomly assigned to groups

• No reason to assume that ppts with one characteristic would be more/less likely to end up in one of the groups

• Groups are expected to be constant with respect to extraneous variables.

What do you use when random allocation is impossible?

• natural groups design- use naturally occurring groups e.g. smoker/non-smoker. Does not keep potential confounders constant.

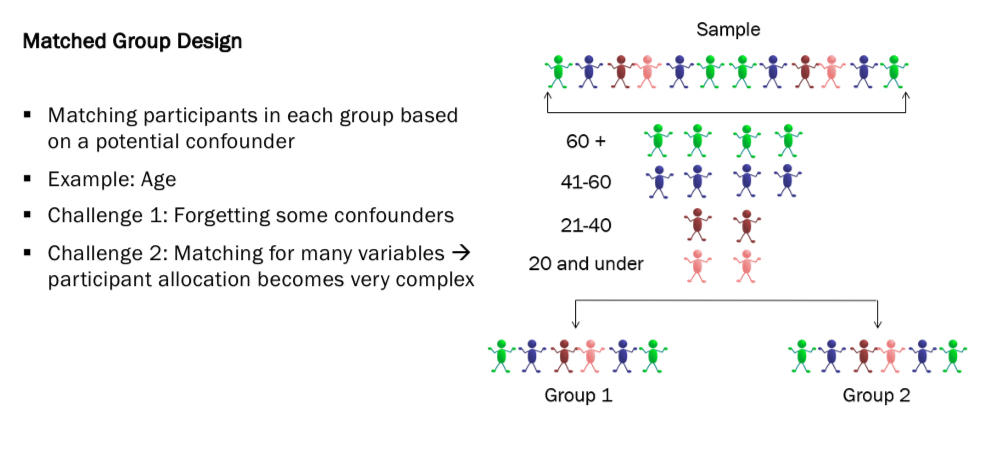
• Matched groups design- matching ppts in each group based on a potential confounder

What are the confounding variables in within-subjects designs?

• time

• Order effects- boredom, practice, habituation, sensitisation, adaptation, comparison

How do you deal with confounding variables in within-subjects design?

Counterbalancing.

• Divide ppts into 2 groups

• In one group, condition 1 is administered first, in the other group condition 2 is administered first.

Incomplete vs complete within-subjects design?

Incomplete within-subjects design

• each ppt experiences each condition only once

• Order of administration varies between ppts

• Practise effects are balanced between ppts

Complete within-subjects design

• each ppt experiences each condition multiple times

• Order of administration varies within ppts

• Practise effects are balanced within ppts

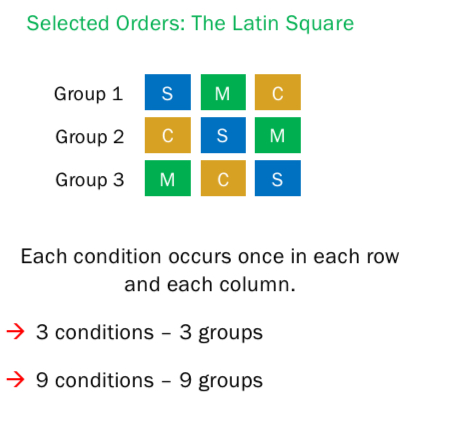
When do counter-balancing methods differ?

It depends on how many permutations (combinations) of conditions are being considered.

• if there aren’t many conditions, it is easy to do all possible orders

• When there is a large number of conditions, the number of possible permutations becomes unmanageable, so use selected orders e.g. the Latin Square