C1 Simple Harmonic Motion

SHM

C1.1 UCM

UCM = object going around in a circle at constant speed. Usually horizontal circle.
Although speed is constant, still accelerating; centripetal acceleration due to centripetal force, eg. tension in a string.

C1.2 SHM

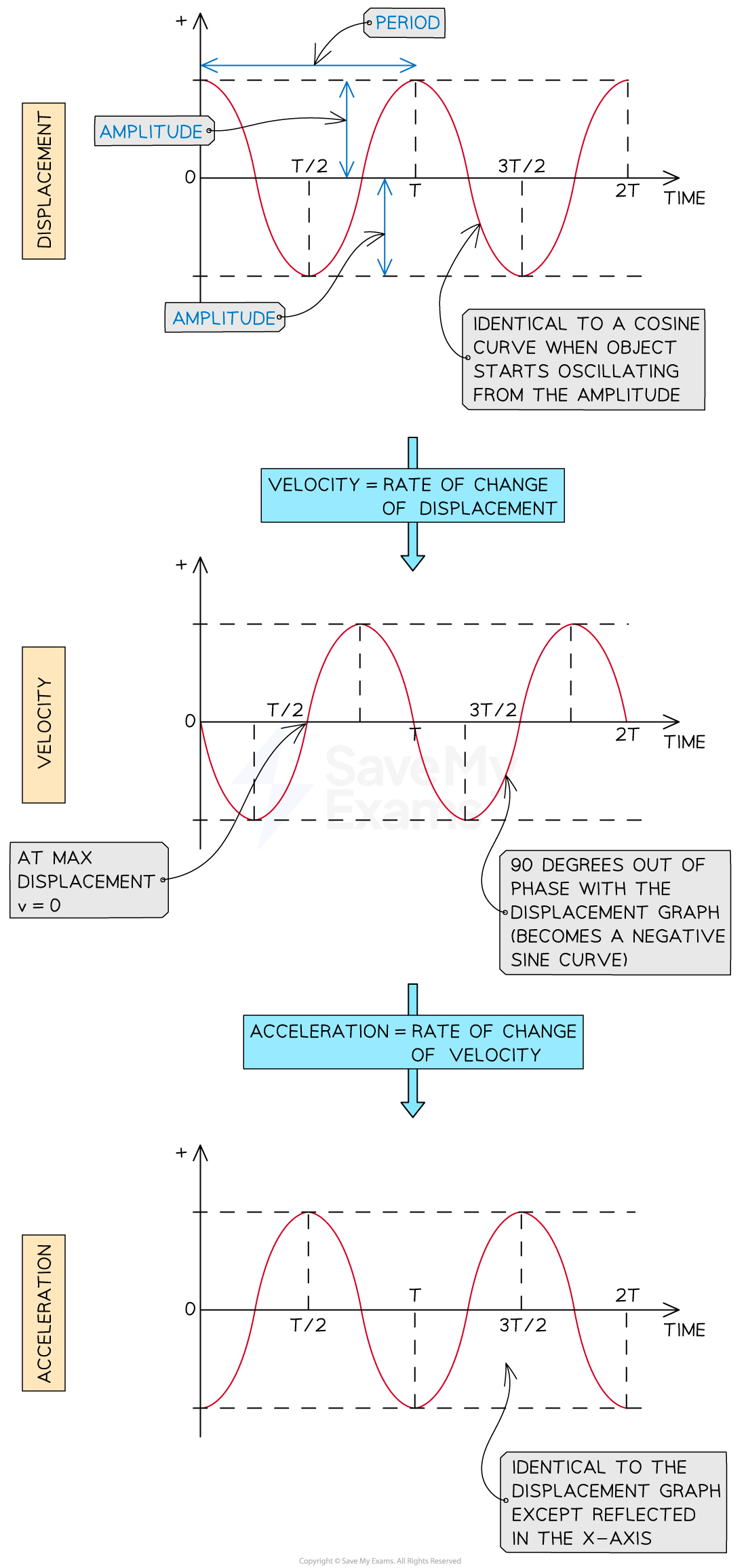
Repetitive movement back and forth through equilibrium. Uniform time period:periodic.
Restoring force directed towards equilibrium, directly prop to distance from it.

C1.3 Oscillation

Repetitive variation with time t of displacement x of object about equilibrium (x=0)

Eg. Pendulum oscillates between A and B, give x-t graph of a sin-wave.

C1.4 Equilibrium position

x=0, no resultsnt force acting on object. Fixed central point that object oscillates around

C1.5 Displacement (from equil)

Horizontal or vertical distance of a point on the wave from its equilibrium position. Vector, meters, + or -

C1.6 Period (T)

Time period → time interval for 1 complete oscillation measured in s. Constant period: isochronous

C1.7 Amplitude (x_o)

x_o = max value of x on either side of equilibrium position. in meters.

C1.8 Frequency (f)

f = nr of oscillations per second (Hertz;Hz = s^-1)
f = ¹/_T

C1.9 Angular Frequency (ω)

ω = angular frequency = rate of change of angular displacement over time: rad s^-1

ω = 2π/T = 2πf

C1.10 Condition SHM

a ∝ -x
Restoring F(or a) is opposite and directly proportional to the displacement form the equilibrium position

C1.11 Graph SHM

See, period, amplitude, min/max velocities

C1.12 Simple pendulum and mass-spring

1. Side to side fixed point, consider long ass string so its mostly horizontal motion, not vertical. T = 2π √(^l/_g)

   1. Small angle approximation → sinθ = θ

2. Mass spring; vertically up horizontally down; magnitude of amplitude dependent on spring. F_H = -kx. T = 2π √(^m/_k)

C1.13 Equations of a

a = -ω²x

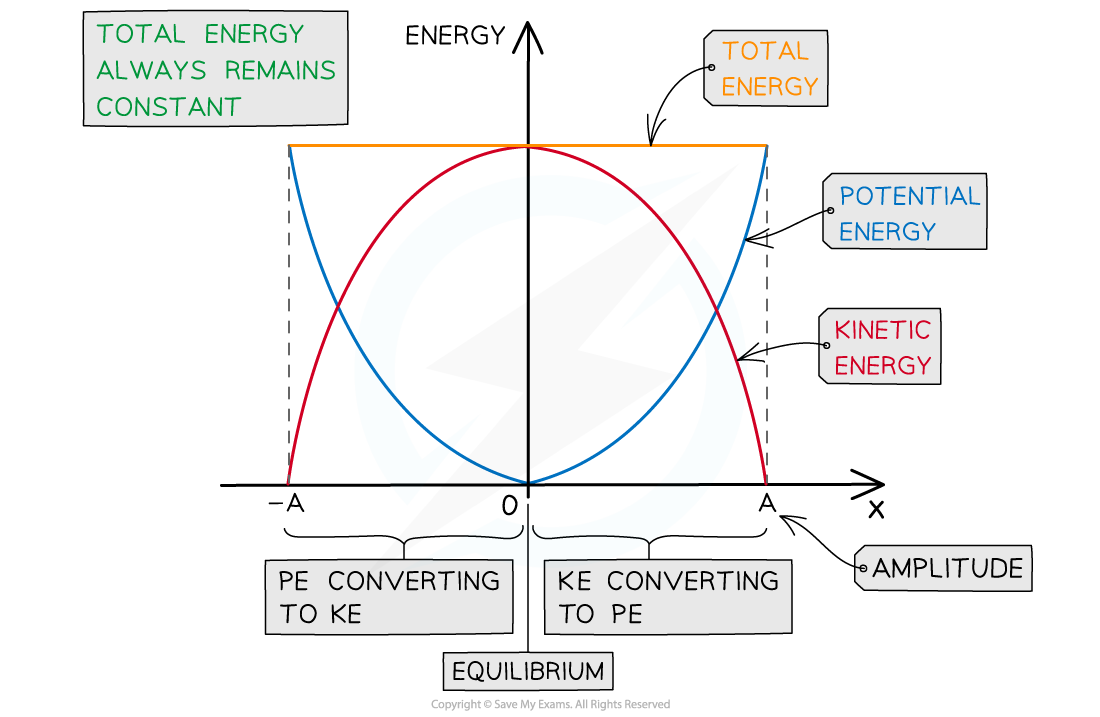
C1.14 Energy change in SHM

Interplay between E_k and E_p (gravitational, elastic)
Total energy doesnt change. E_p + E_k = constant E_p
½ mω²x² = E_P
½ mω²x_o² = E_T

½ mω² (x_o² - x²) = E_T

C1.15 Equations SHM

x = x_o sin ωt
v = ωx_o cos ωt = - ωx_o sin ωt
a = -ω²x_o sin ωt

v = ± ω √x_o² - x²

C1.16 Phase difference

In phase; same point in wave cycle. Difference between points angles stuff yk… is phase angle. If no starts from equilibrium, out of phase by Φ. Diff in angular displacement compared to oscillator which has x=0 and t=0. Between 0 and 2π.

Graphically:

x = x_o sin (ωt+Φ) - also for the others, just add a phi
v = ωx_o cos (ωt+Φ)
a = -ω²x_o sin (ωt+Φ)

Φ = phase difference = how far the point move TO THE LEFT
Starting position: “time from the equilibrium”