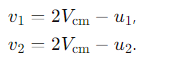5- Third law of Newton, conservation of momentum, and centre of mass

What does Newton's Third Law of Motion state?

An action is always opposed by an equal and opposite reaction; or, the mutual actions of two bodies are always equal and act in opposite directions."

In Newton's Third Law, how are action and reaction forces related?

Action and reaction forces are:

1. Equal in magnitude.

2. Opposite in direction.

3. Always present as a pair due to an interaction.

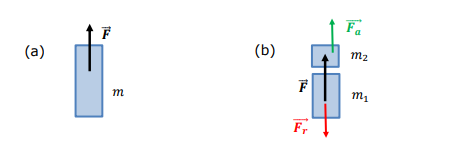
Write Newton's Second Law for the engine and cabin separately.

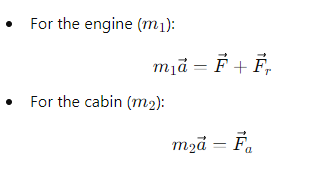
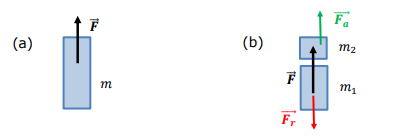
What equation describes the combined motion of the engine and cabin?

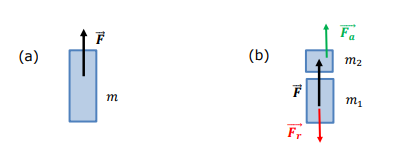
How do the action and reaction forces relate in the spacecraft system?

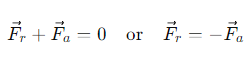
What is the formula for impulse in the context of Newton's Second Law?

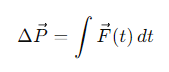
How is the change in momentum (ΔP⃗) related to impulse?

The change in momentum of a particle equals the impulse applied to it

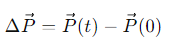
What is the formula for impulse when time-averaged force is considered?

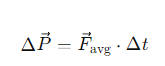
What does the area under the force-time graph represent?

The impulse of the force.

What is the total momentum of a system of particles?

The sum of the momenta of all individual particles in the system

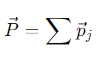
How is the total momentum of a system related to external forces?

The time derivative of the total momentum equals the total external force acting on the system

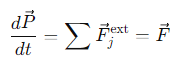
Why do internal forces not affect the total momentum of a system?

Internal forces within the system occur in action-reaction pairs and cancel out in the summation

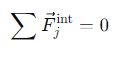
What does the equation dP⃗/dt=F⃗ imply about a system with no external forces?

If F⃗=0 the total momentum of the system is conserved

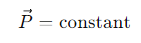
How do Newton's laws contribute to the momentum conservation principle in a system?

• The third law ensures internal forces cancel

• The second law relates the external forces to the rate of change of momentum.

What does the law of conservation of momentum state for an isolated system?

In an isolated system (where no external forces act), the total momentum is conserved

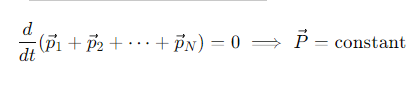
What condition must be satisfied for momentum conservation to apply?

The system must be isolated, meaning no external forces act on it

How does the projection of momentum relate to conservation laws?

The component of total momentum perpendicular to any external force is conserved

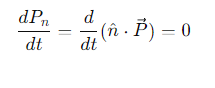
What characterizes an elastic collision?

Both total momentum and total kinetic energy of the system are conserved.

What happens to kinetic energy in an inelastic collision?

Some kinetic energy is converted to other forms of energy → not conserved

How can external forces typically be treated during a collision?

During a collision, the interaction forces are strong, so external forces are often negligible.

What is the equation for the position of the centre of mass (R_cm)

m_j​ and r_j are the mass and position of each particle in the system.

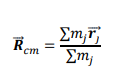
How is the total momentum of a system related to its centre of mass?

M = the total mass

v_cm= the velocity of the centre of mass.

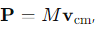
How is the total acceleration of the system's centre of mass (a_cm​) related to external forces?

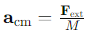
How does the centre of mass behave in the absence of external forces?

The centre of mass moves with constant velocity.

What is a central force?

A force that depends only on the relative distance between two particles and is directed along the line joining them

What is the equation for the relative displacement in a two-body problem?

r_1​ and r_2​ are the positions of the two particles.

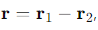
What is the equation for the centre of mass velocity V_cm?

m_j​ and v_j​ are the mass and velocity of each particle.

What is the equation for the reduced mass μ of a two-particle system?

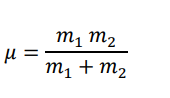
Why is the reduced mass always less than the mass of either particle (μ<m₁ and μ<m₂​)?

Because the formula involves the product of masses divided by their sum, which is always smaller than either mass.

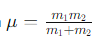
What is the equation of motion for the reduced mass?

F(r) = the central force acting between the two particles.

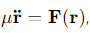
How does the total momentum conservation relate to the centre of mass in the two-body problem?

For an isolated system, the centre of mass moves with constant velocity.

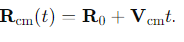
What is the equation of the position of the centre of mass for two particles?

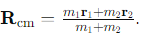
What equation describes the position of the first particle in terms of the centre of mass and relative displacement?

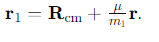
What equation describes the position of the second particle in terms of the centre of mass and relative displacement?

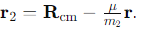
How is the velocity of the first particle expressed in terms of the centre of mass velocity and the relative velocity?

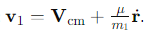
How is the velocity of the second particle expressed in terms of the centre of mass velocity and the relative velocity?

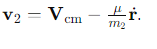
What is the equation for the total kinetic energy of two particles?

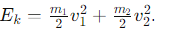
How can the total kinetic energy be decomposed into two terms?

E_cm​ = the kinetic energy of the centre of mass

E_rel=​ the kinetic energy of relative motion.

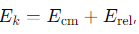
What is the equation for E_cm​, the kinetic energy of the centre of mass?

V_cm​ =the velocity of the centre of mass.

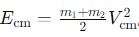
What is the equation for E_rel​, the kinetic energy of relative motion?

μ=the reduced mass

v_rel= the relative velocity.

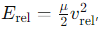
How is the relative velocity v_rel defined in terms of particle velocities?

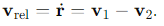
What happens to E_cm during a collision?

It remains conserved because the velocity of the centre of mass does not change.

Under what condition is E_rel conserved during a collision?

it is conserved in elastic collisions, where the total kinetic energy is conserved.

What is the key characteristic of the centre of mass (COM) in the COM frame?

The centre of mass is always fixed at zero in the COM frame.

What is the total momentum of the system in the COM frame?

The total momentum in the COM frame is always zero

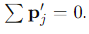
How are the initial velocities of two particles related in the COM frame?

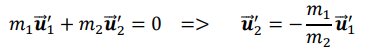
How are the final velocities of two particles related in the COM frame?

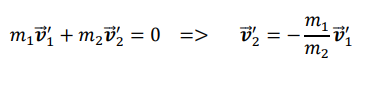
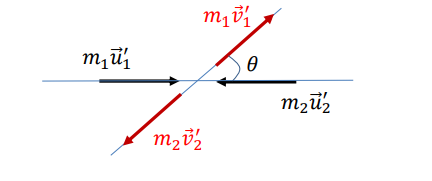
What happens to the directions of motion of the particles in the COM frame?

The particles always move in opposite directions, both before and after the collision.

What is true about the magnitudes of the particle velocities in an elastic collision in the COM frame?

The magnitude of each particle's velocity remains constant

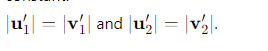
What are the possible scattering angles θ in a one-dimensional elastic collision?

• θ=0 (particles do not collide)

• θ=π (particles reverse direction after collision).

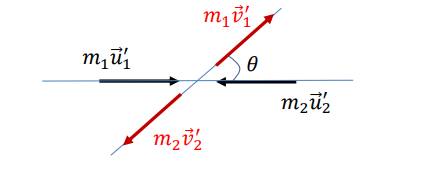
In the lab frame, how are the final velocities of the particles expressed in terms of V_cm?