Logique - Synthèse
4.0(1)
Studied by 5 people4.0(1)
Call Kai
Learn
Practice Test
Spaced Repetition
Match
Flashcards
Knowt PlayCard Sorting
1/22
Earn XP
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
23 Terms
1
New cards
¬
négation(non)
2
New cards
∨
disjonction (ou)
3
New cards
∧
conjonction(et)
4
New cards
⇒
implication (si...alors...)
5
New cards
⇔
équivalence (...si et seulement si ...)
6
New cards
Tautologie
Une formule toujours vraie
7
New cards
L'équivalence entre formules
Ф1 ⇔ Ф2 \=\> une tautologie
8
New cards
∀
pour tout
9
New cards
∃
il existe
10
New cards
La contraposée de P⇒Q
¬Q ⇒ ¬P
11
New cards
La réciproque de P⇒Q
Q ⇒ P
12
New cards
Prouver que la formule Ф est fausse
Prouver que ¬Q est vrai
13
New cards
Preuve par induction de P(x)
Case de base P(0)
Cas général: P(n) = P(n+1)
Cas général: P(n) = P(n+1)
14
New cards
Un ensemble
Une connection d'objet appelés éléments
15
New cards
Un ensemble en extension
Les éléments distingués explicitement. Ex: {a,b}
16
New cards
Un ensemble en compréhension
formules qui décrit exactement les éléments de l'ensemble. Ex: {x | P(x)}
17
New cards
f: A → B, f est injective
∀ a1,a2 € A; f(a1)\=f(a2) ⇒ a1\=a2
18
New cards
f: A → B, f est surjective
∀ b € B, ∃ a € A f(a)\= b
19
New cards
Surjective
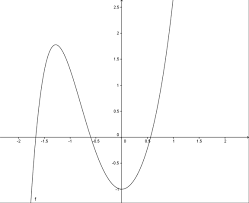
20
New cards
Injective
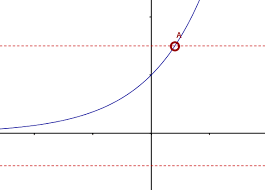
21
New cards
¬(P⇒Q)
P ∧ ¬Q
22
New cards
√(x)\=y
(y²\= x ∧ y ≥ 0 )
23
New cards
F est croissante
∀a,b ∈ Dom f, a≤b →f(a)≤f(b)
Note 
Flashcards (103)