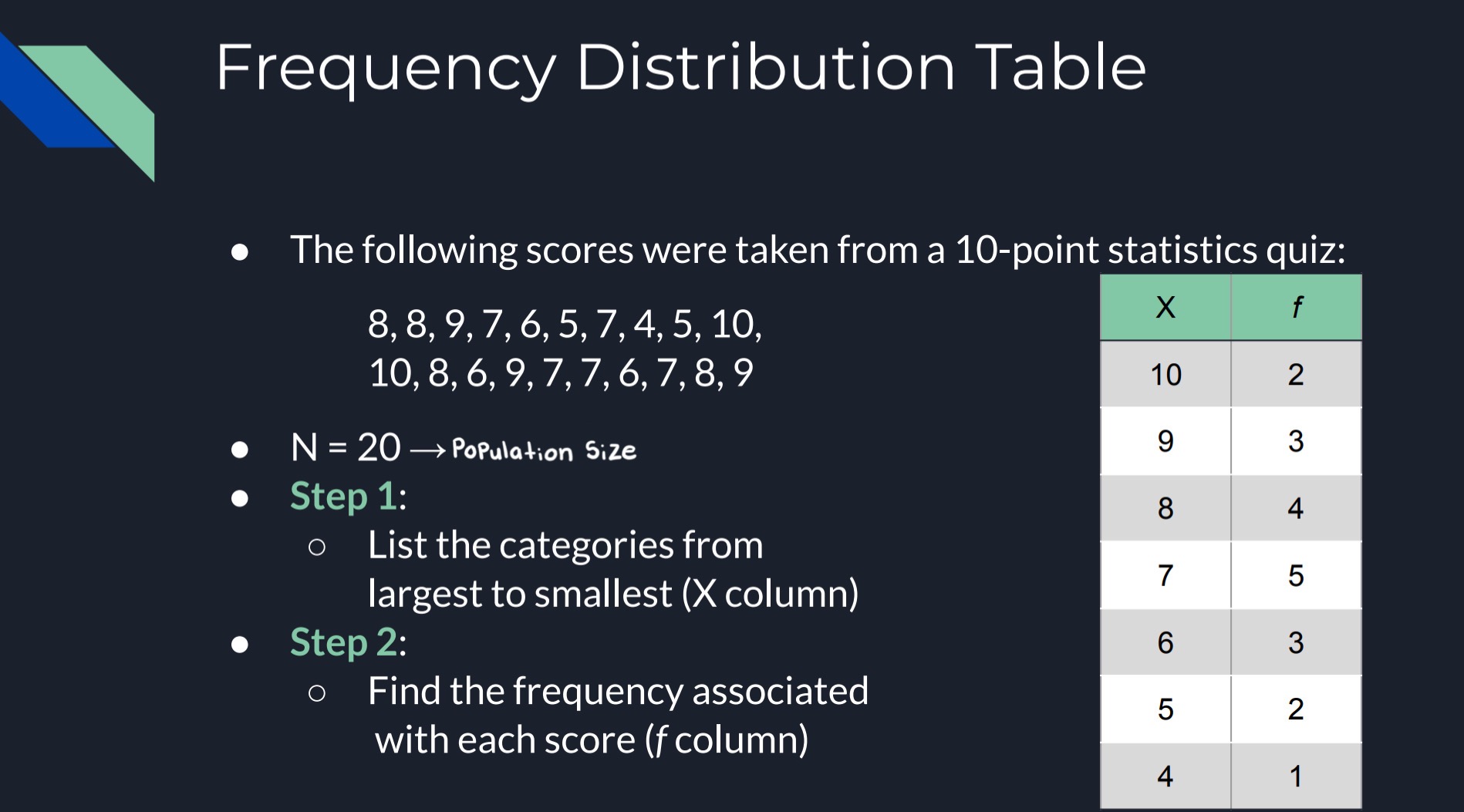
Frequency Distribution

Frequency Distribution

• Provides an organised tabulation of the number of individuals located in each category on the scale of measurement

• Table or Graph; Various forms of graphs that can be utilised

NOTE: You can find the N (population/total participants) by summing only your entire frequency

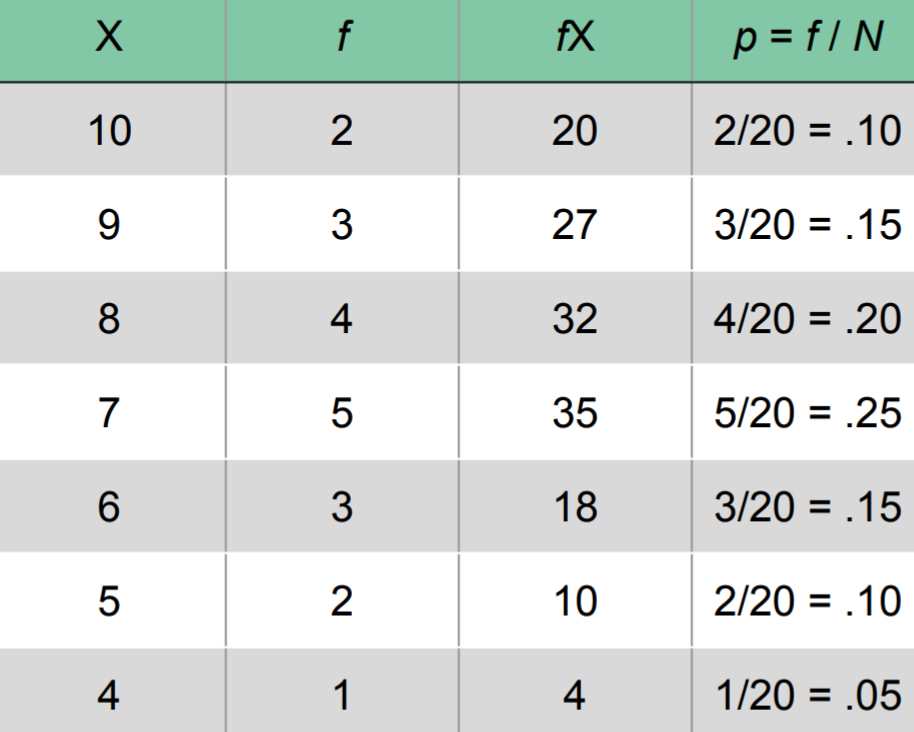
Calculation Frequency Distribution (Table)

• Multiply your X variable by your f (frequency)

• Sum all numbers together

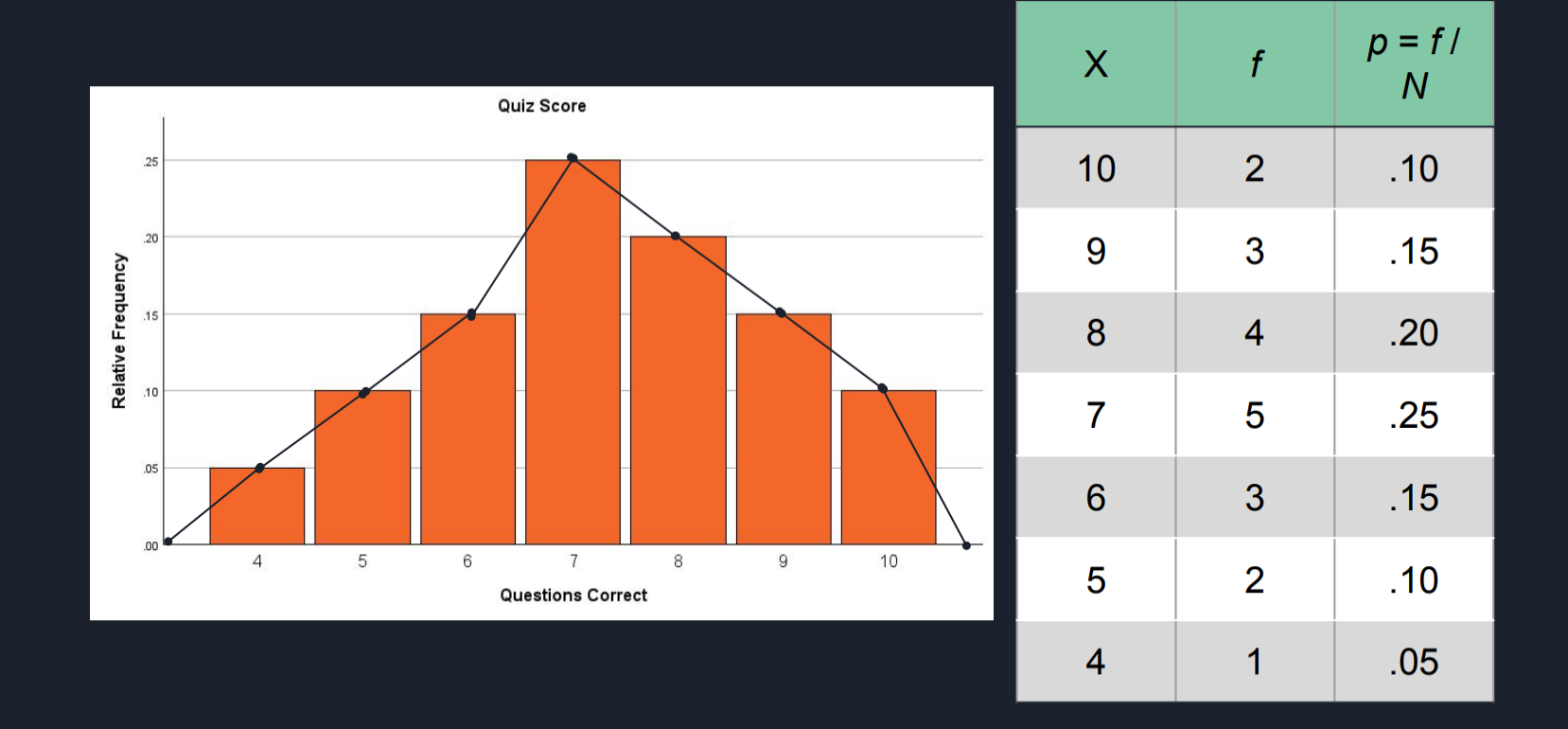
Proportions (Relative Frequency)

Measures the fraction of the total group that is associated with each score

FORMULA: P = f/N

• Proportions are also known as relative frequencies because proportions describe the frequency (f) in relation to the total number (N)

Percentages

Two Ways to Calculate

1. Do the Formula; P = f/N *(100)

OR

2. From your Proportions calculation, you move the decimal over right twice; P*(100)

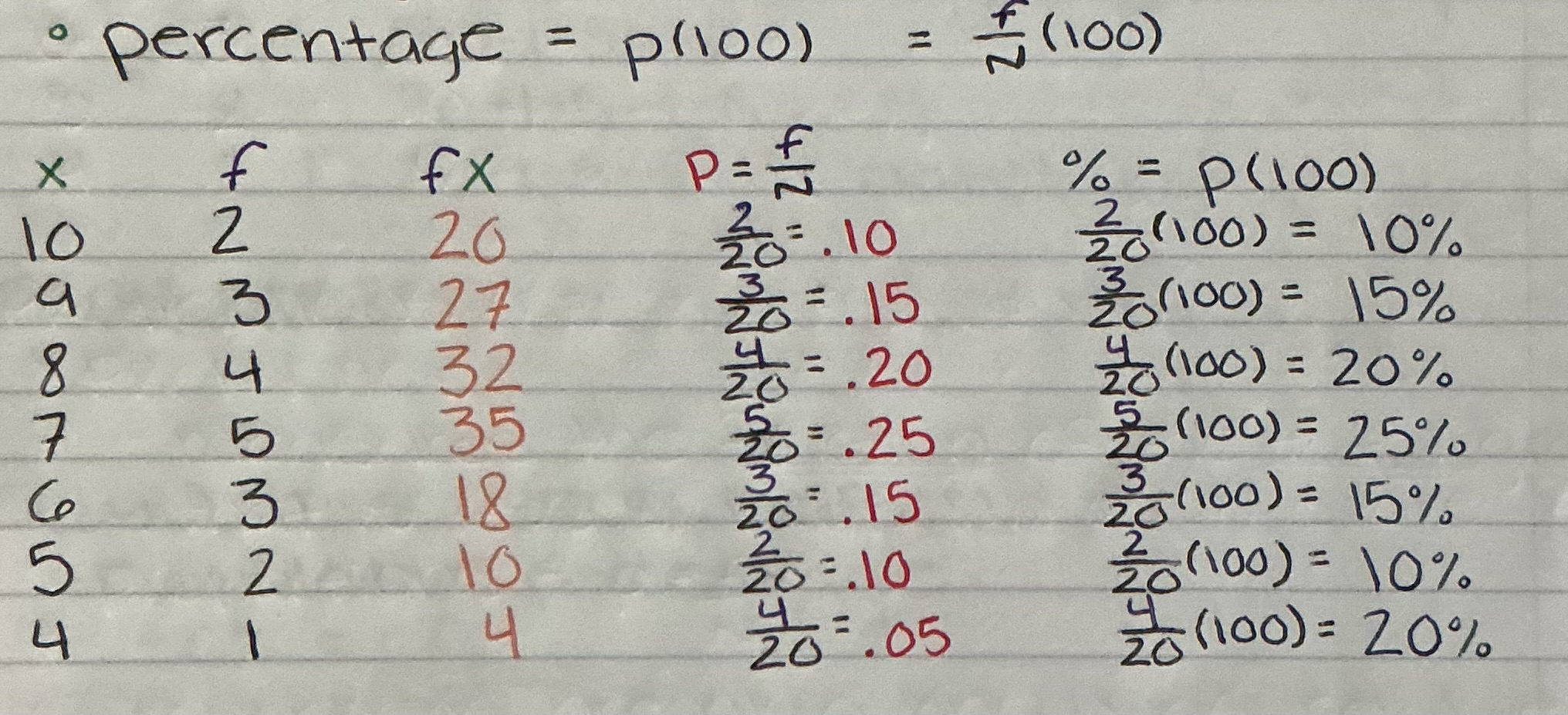
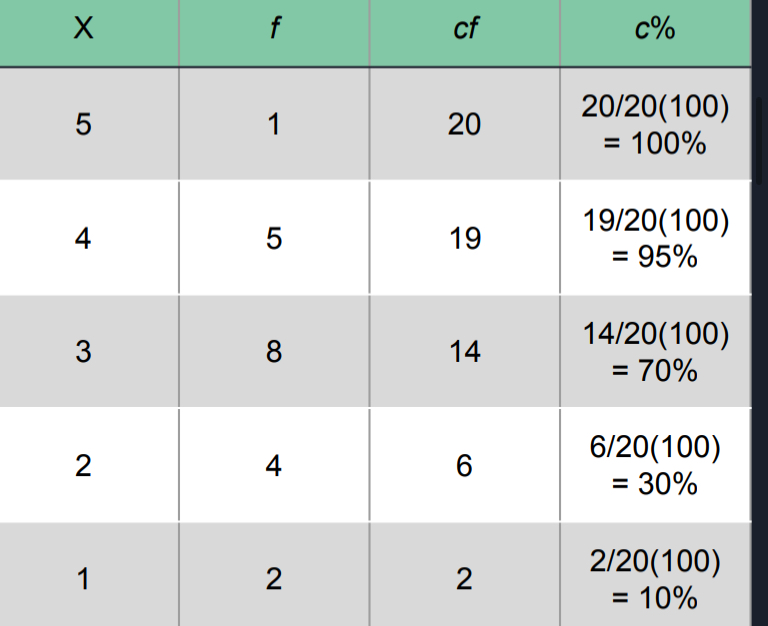
Cumulative Frequency (cf)

1. Your top value will be your N (total population)

2. Going down, you will subtract by the last frequency above (you will keep summing the frequencies as you go down and subtract by your N from that row, or your last calculated cumulative frequency); kinda like going diagonally \

3. Your bottom value will be the same as your bottom value frequency

Cumulative Percentages (c%)

FORMULA: c% = cf/N *(100)

• Real Limits; Interpret c% as the % of individuals accumulated by the time you reach the top of the interval (the upper real limit)

Grouped Frequency Distribution Tables

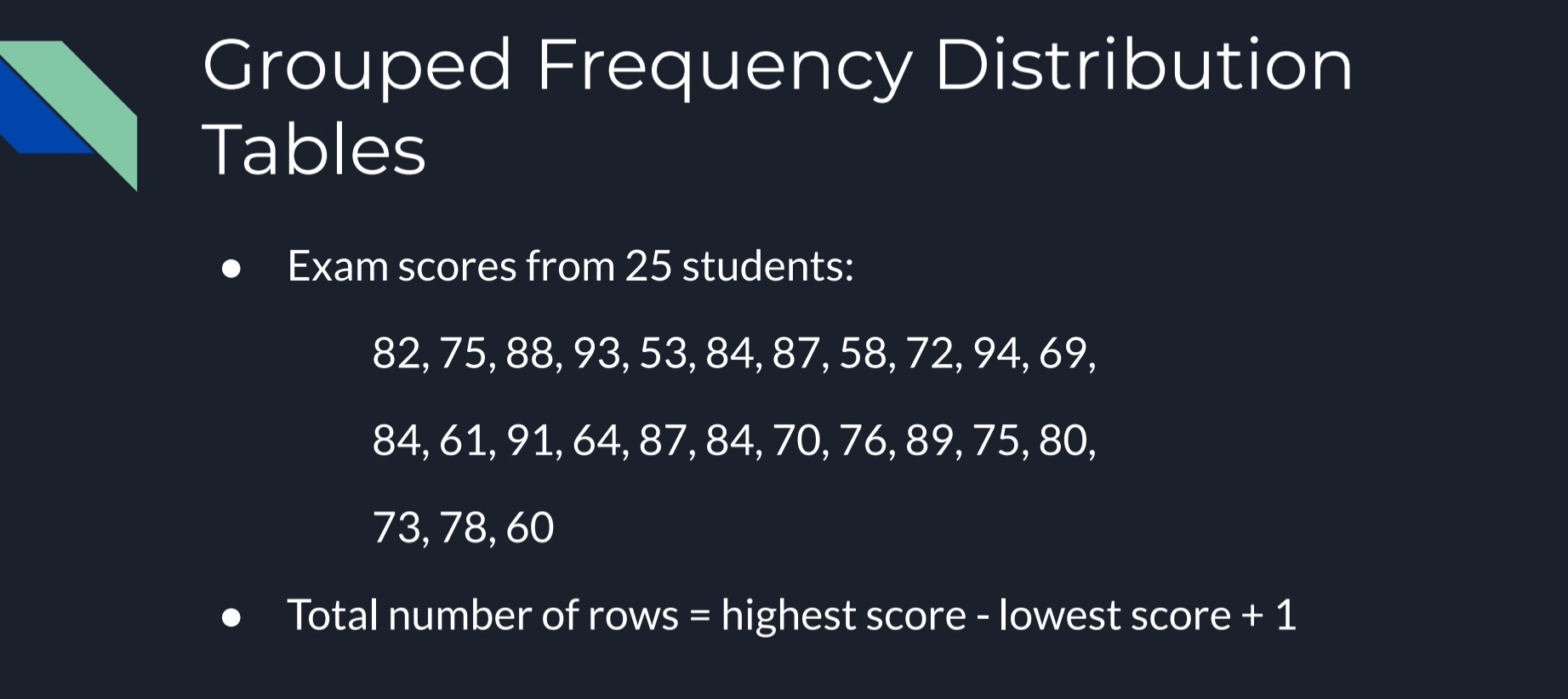
EXAMPLE

1. You have all different types of exam scores from your all your participants (N)

2. To get total number of rows, you take your highest score and subtract it by your lowest score and add one

3. 94(highest score) - 53(lowest score) + 1 = 42 (range of score)

Grouped Frequency Distribution Table (shown continuation)

• On a table, you need the proper construction rules so that the data is easy to read (42 is your range of score)

1. Table should have about 10 class intervals

2. Width of each interval should be a simple number (i.e., 2, 5, 10, or 20)

3. Bottom score of each interval should be a multiple of the width

4. All intervals should be the same width

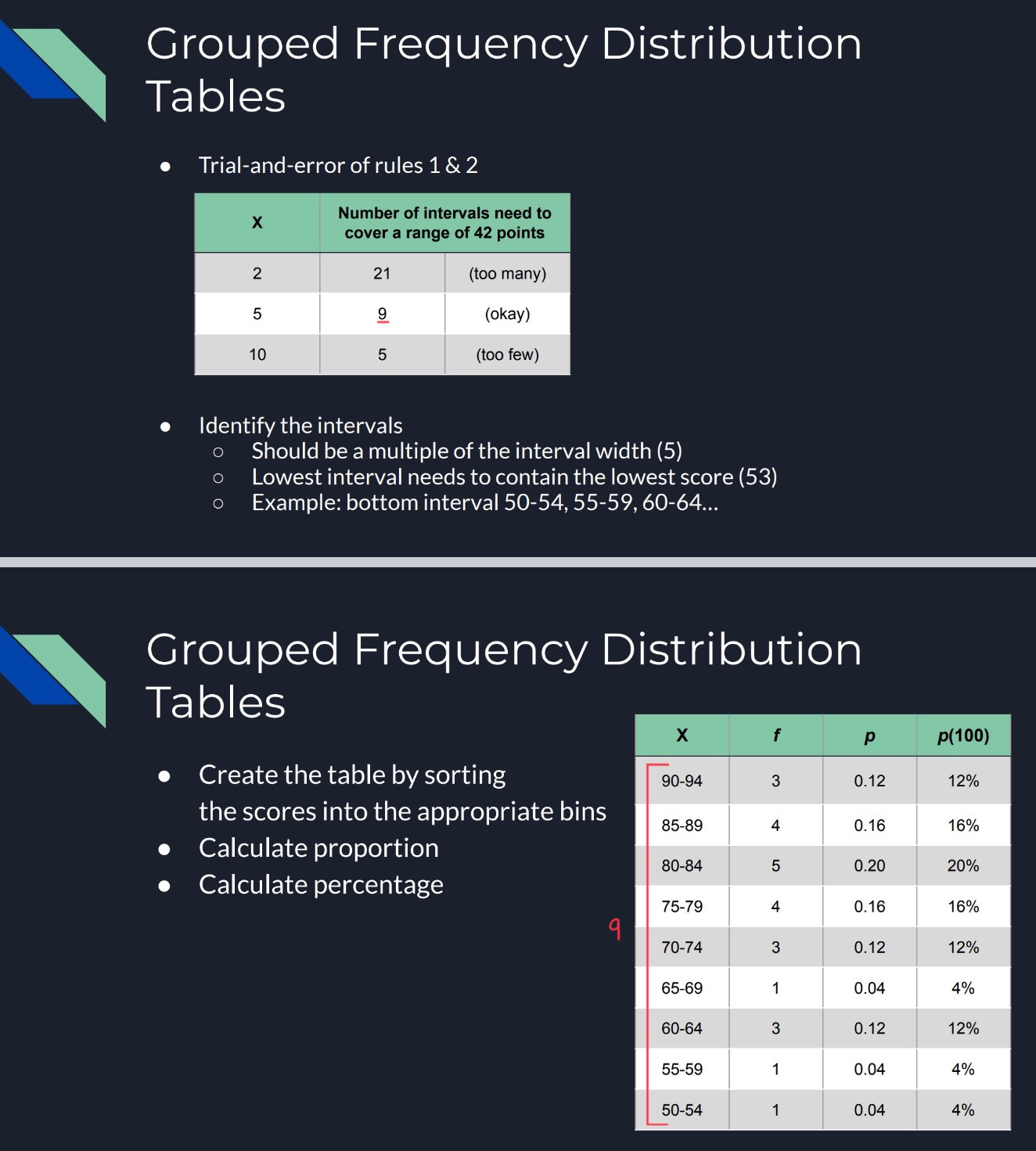
Real Limits

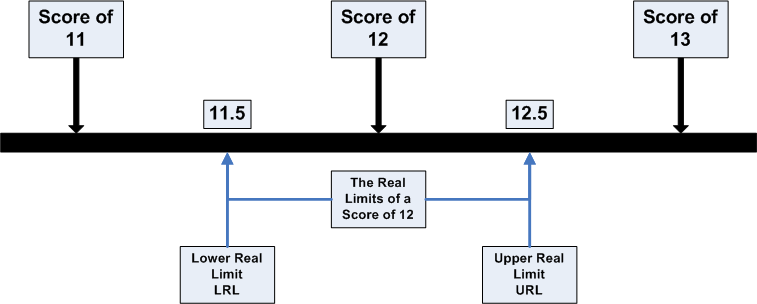
• The boundaries of intervals for scores that are represented on a continuous number line

• The real limit separating two adjacent scores is located exactly halfway between the scores

• The upper limit is at the top of the interval, the lower real limit is at the bottom

EXAMPLE) differentiate 150 from 149 and 151

- X = 150

- Upper real limit = 150.5

- Lower real limit = 149.5

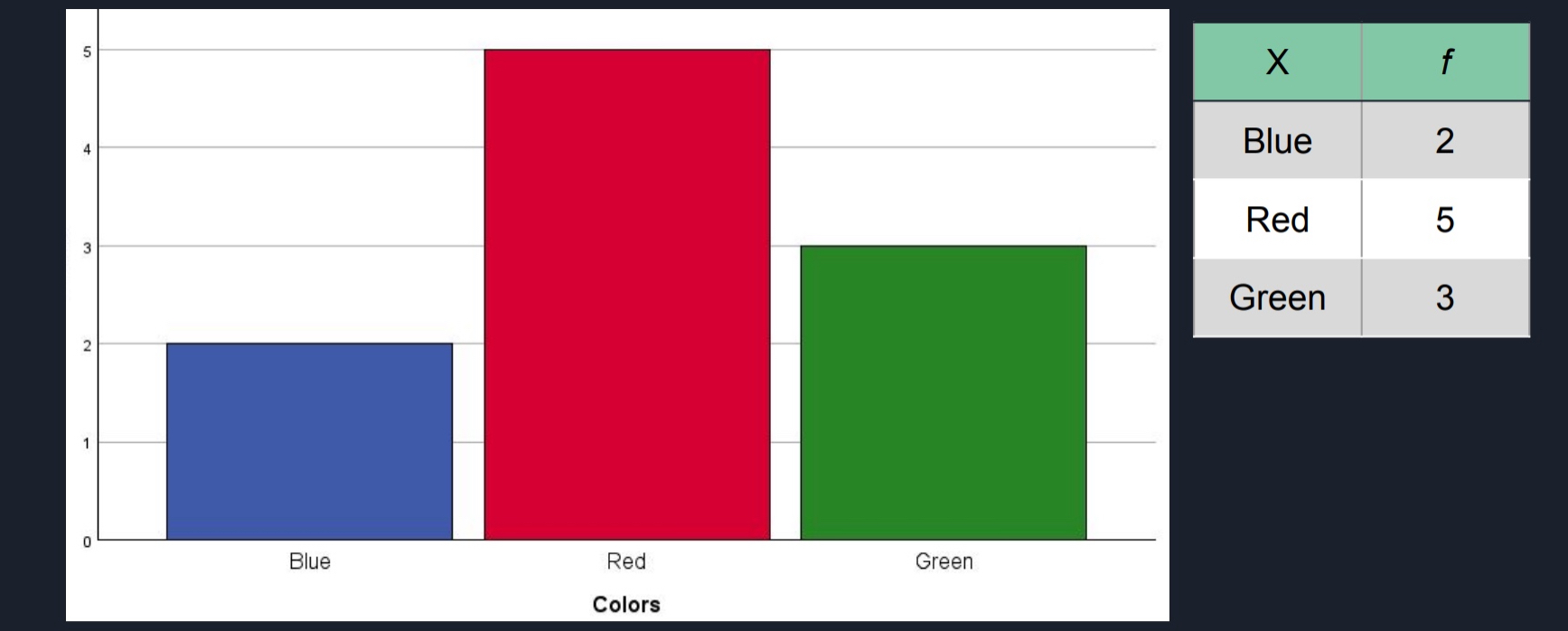
Bar Graphs

Used for Nominal or Ordinal level data

Frequency Distribution Graphs Histograms or Polygons

• Designed for interval or ratio data

• Construction Steps

  • List the numerical scores or intervals on the X-axis

  • Draw a bar above each X value so that:

    • The height of the bar corresponds to the frequency for that category

    • The width of the bar extends to the real limits of the category

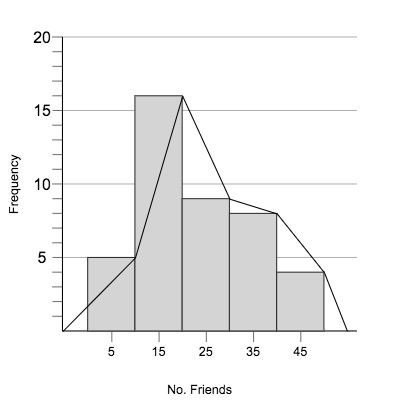
Frequency Distribution Graphs: Polygons

1. A dot is centered above each score so that the vertical position on the plot corresponds to the frequency for the category

2. A continuous line is drawn from dot to dot, connecting the entire series

3. Begin line and end line at the X-axis

Different Types of Distributions

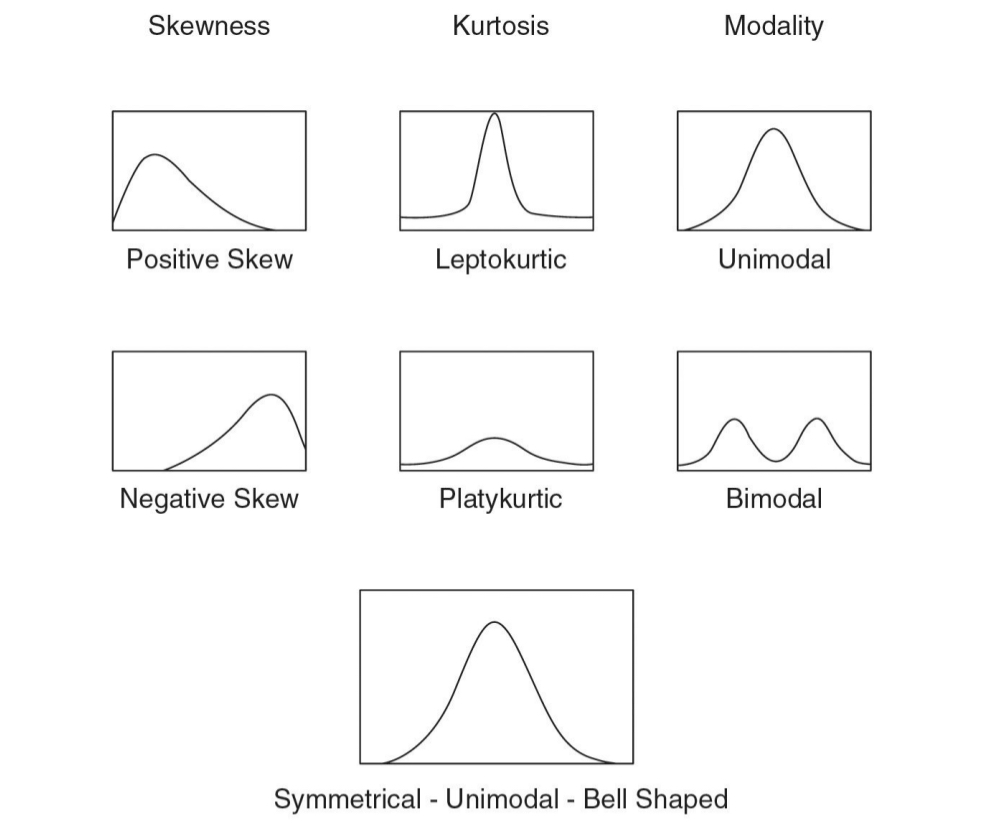
Symmetric Distributions

It is possible to draw a vertical line through the middle of the distribution so that one side of the distribution is a mirror image of the other

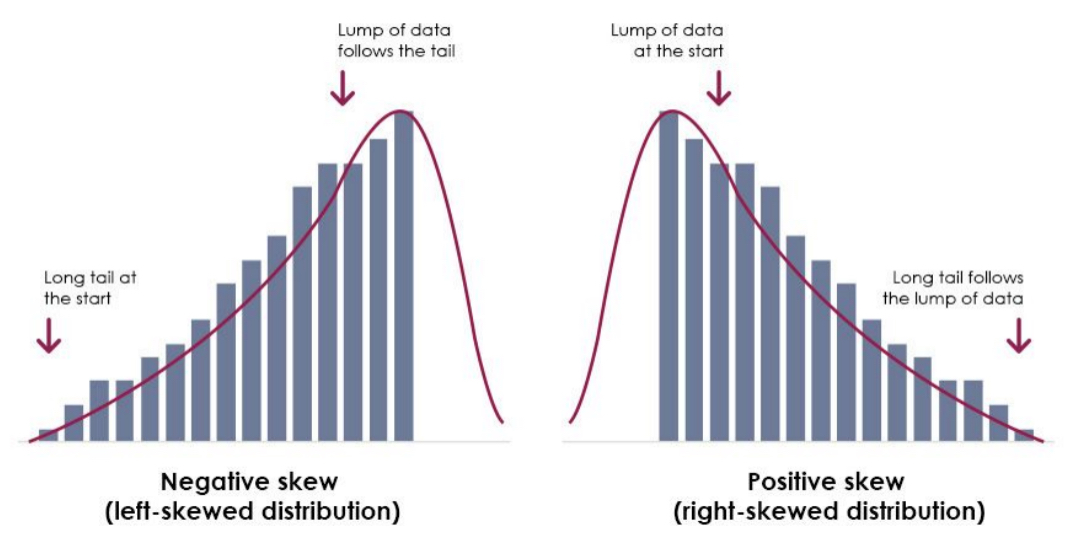
Skewed Distributions

The scores tend to pile up toward one end of the scale and taper off gradually at the other end

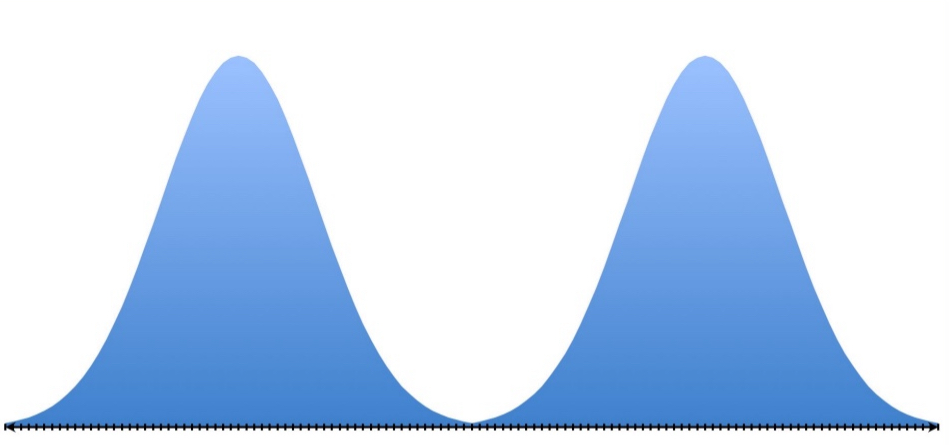
Bimodal

Mode: The most common score

• Corresponds to the highest point in the distribution

Bimodal: a distribution with two modes

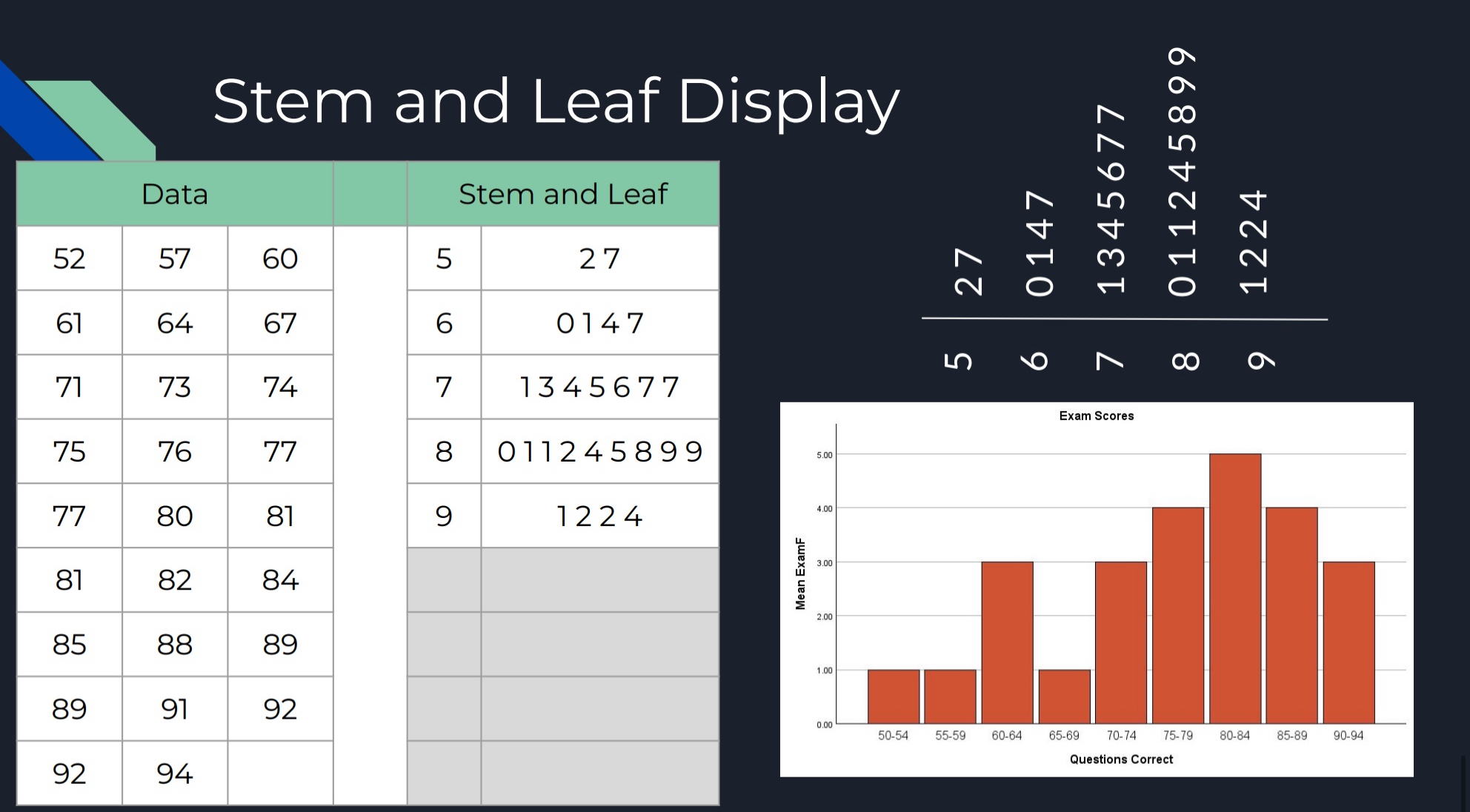
Stem and Leaf Display

• Alternative to a frequency distribution

• Separate the scores into two parts

STEM: the first digit (or digits if it’s in the tens, hundreds, etc.)

LEAF: The last digit