Flashcards from Practice Exam

Inequalities involving Absolute Values:

|u| < a means. . .

-a <u <a

inequalities involving Absolute Values:

|u| ≤ a means. . .

-a ≤ u ≤ a

inequalities involving Absolute Values:

|u| > a means that. . .

a: u < -a or u > a

inequalities involving Absolute Values:

|u| ≥ a means that. . .

: u ≤ -a or u ≥ a.

inequalities involving Absolute Values:

|2x-3| ≤ 5

1st: Y1= |2x-3|

2nd: Y2= 5

Find X-intercepts:

“ -1 ≤ x ≤ 4

inequalities involving Absolute Values:

|3x+4|-5 >0

means that 3x + 4 < -5 or 3x + 4 > 5.

3x + 4 < -5

• Minus 4 on both sides: 3x< -9

• Divide both sides by 3

• x< -3

3x + 4 > 5.

• minus 4 on both sides: 3x> 1

• Divide both sides by 3:

• x> 1/3

inequalities involving Absolute Values:

|x+5| <12

1st: Y1= |x+5|

2nd: Y2= 12

3rd: Find x-intercepts: -17 < x < 7

|u| < a

-u < x < u

|u| > a

x <u, x>u

Transformation of graphs:

f(x) + k

graph is shifting up by k units

Transformation of graphs:

f(x) -k

Graph is shifting down by k units

Transformation of graphs:

f(x+k)

Graph is moving horizontally left

Transformation of graphs:

f(x-k)

graph is moving horizontally right

Transformation of graphs:

af(x), |a|>1

graph is vertically stretched

Transformation of graphs:

af(x), |a|: 0<|a|<1

graph is vertically compressed

Transformation of graphs:

f(x) → -f(x)

graph is reflected across the x-axis

Transformation of graphs:

f(x) → f(-x)

graph is reflected across the y-axis

Transformation of graphs:

Steps:

1st: Graph y= square root of x

2nd: Since its moving horizontally right, it must be (x-7)

3rd: Since its being reflected across the x-axis, the negative sign must be outside the equation

Final answer: -f(x-7)

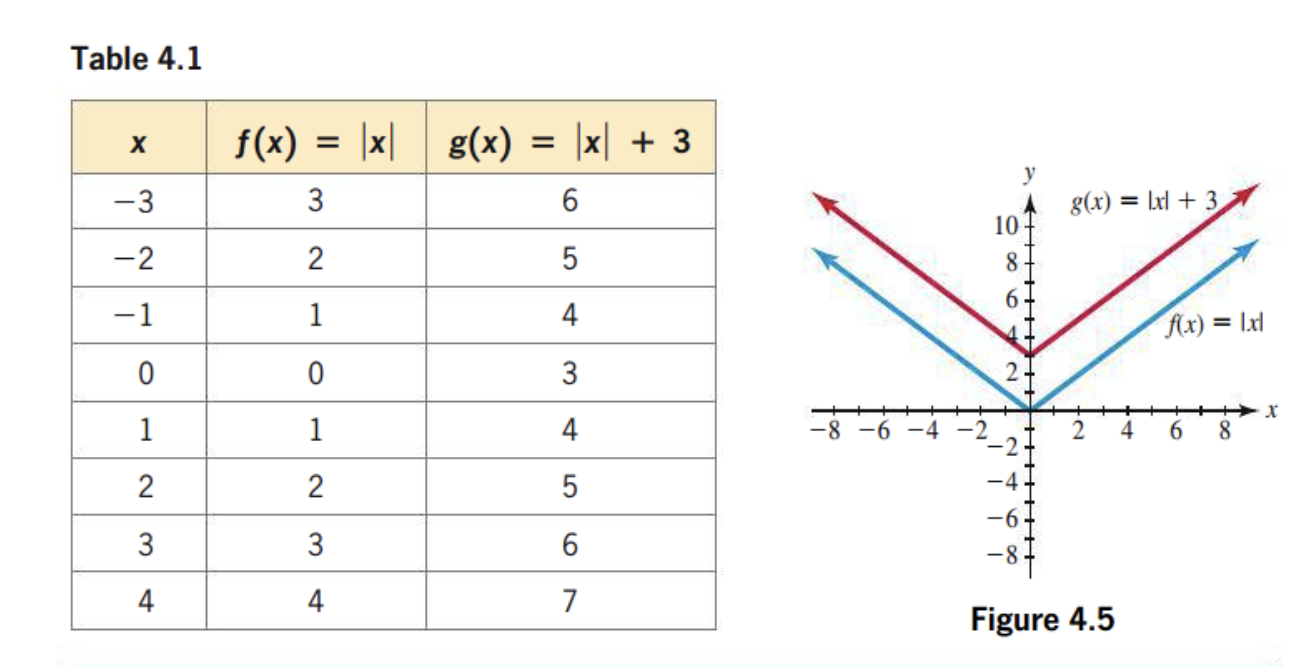
Whats happening here?

|x| +3: means that the graph is shifting up by 3 units.

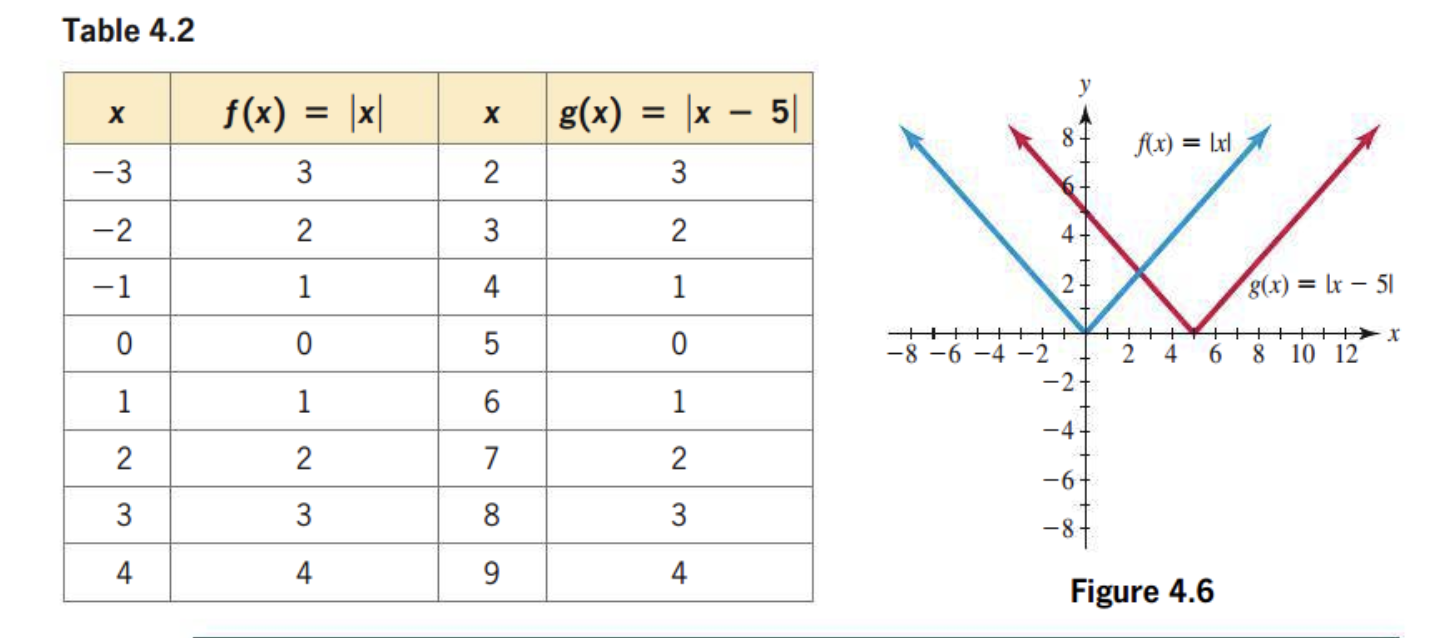
Whats happening here?

|x-5|: the graph is moving right by 5 units.

|x-k|

Moving right

|x+k|

Moving left

f(x)+k

Moving up

f(x)-k

Moving down

steps for inverse functions:

• change f(x) with y

• interchange x and y values

• solve for y

• y=5x+2

• x=5y+2

• x-2=5y (Minus 2 on both sides

• x-2/5 =y (Divide both sides by 5)

Steps for finding the inverse of functions

How to see if a graph is a 1-1 function?

If the graph passes the horizontal line test, it is a 1-1 function

Symmetry with respect to y-axis.

For every (x,y) point there is a (-x,y) point: This is also considered an even function

Symmetry with respect to the x-axis

For every (x,y) point there is a (x,-y) point.

Symmetry with respect to the origin

For every (x,y) point there is a (-x,-y) point: This is also considered an odd function

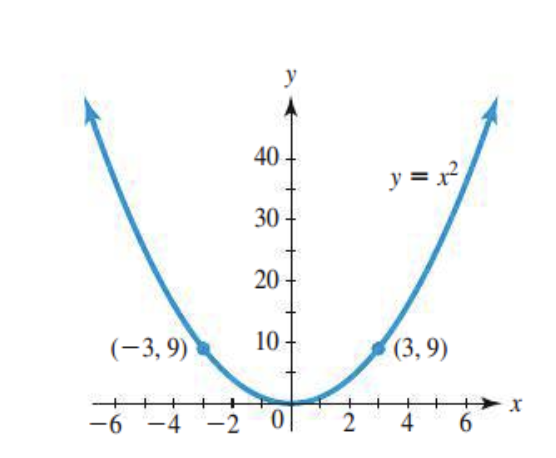
Whats the symmetry of this graph?

This graph exhibits symmetry about the y-axis. (3,9) → (-3,9)

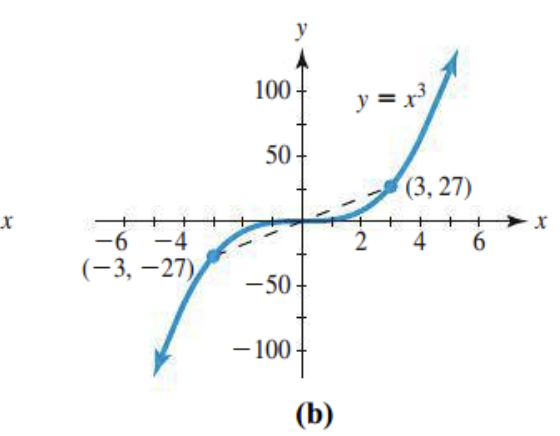
Whats the symmetry of this graph?

This graph is symmetric about the origin. (3,27) → (-3,-27)

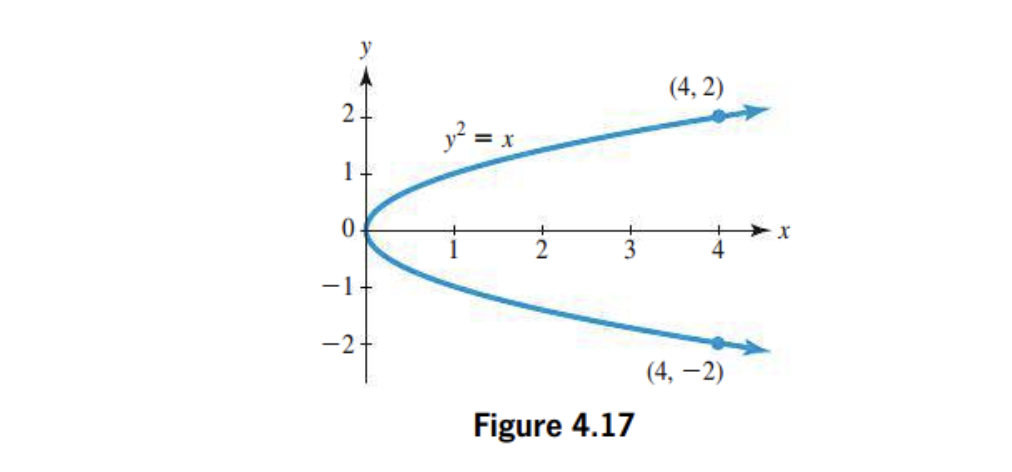
Whats the symmetry of this graph?

This graph shows symmetry about the x-axis. (4,2) → (4,-2)

Operations of functions:

Sum of functions

(f+g)(x)=f(x) +g(x)

Operations of functions:

Difference of functions

(f-g)(x)=f(x) -g(x): Substitute the negative into the second function

Operations of functions:

Product of functions

(f x g) (x)= f(x) times g(x)

Operations of functions:

Quotient

(f/g) (x) = f(x)/g(x)

Operations of functions:

Composition

Find (f-g)(x)

• f(x)= x²-5x

• g(x)=12-x

(f-g)(x) = f(x) - g(x) = (x² - 5x) - (12 - x)

x²-5x-12+x

• x²-4x-12

Compose

f(x)= 3x-4

g(x) =6x+8

Find f(g(4)

1st:

• 6(4)+8= 32

2nd:

• f(32)= 3(32)-4= 92

Solving Quadratic Inequalities:

x²+x+x > 0

• U< x and U>x

Solving Quadratic Inequalities:

x²+2x-3> 0

1st: Graph y=x²+2x-3

Find x-intercepts: -3, 1

Interval Notation (-infinity, -3] U [1, +infinity)

Solve the following

              

• Square both sides: x²=13x

• x²-13x=0 : Set equation to be equal to zero

• x(x-13)=0: Factor

• x=0, x=13

Future value of an Investment with Periodic Compounding formula.

S=P(1+r/k)^kt

What is the future value, to the nearest cent, if $32,000 is invested into an account that pays 5.4% interest compounding monthly for 40 years.

• P=$32,000

• R=5.4→0.054

• k= Monthly, 12

• t= 40

• S=$32,000(1+0.054/12)^(12)(40)

• $ 276,135.15

Future value of an investment with annual compounding

S=P(1+r)^t

Find the future value of $10,000 placed in an account earning 8% per year for 10 years, if interest is compounded annually.

S= $10,000 (1+0.08)^10

= $21,589.25

Find the future value of $10,000 placed in an account earning 8% per year for 10 years, if interested is compounded daily

S=$10,000(1+0.08/365)^(365)(10
= $22,534.46

A)

• 2035-2023= 12 years also our x

• Plus x value into original equation

• 350,000(1.042)^12=

• $573,430.35

B)

• Plus original equation into y= on calculator

• find the y value that corresponds with the doubling of the original value (17 years = $700,000)

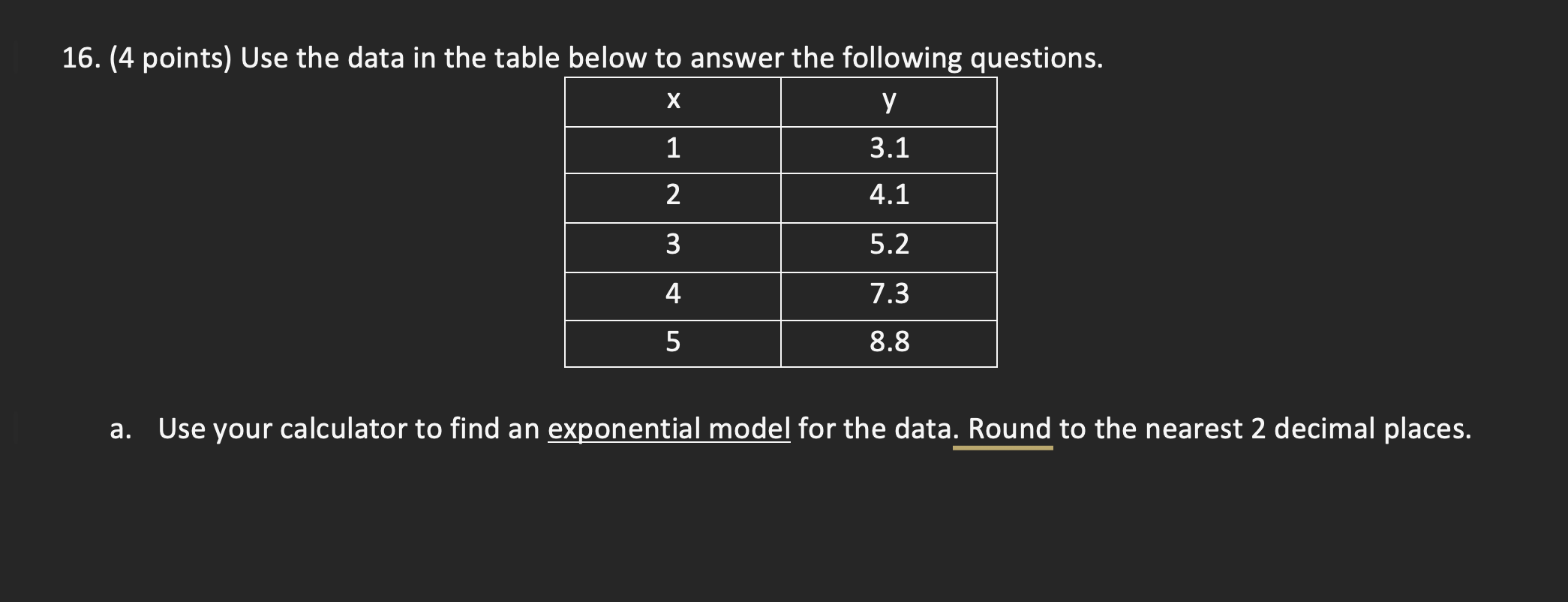
A)

• Plug x and y values into the Calculator

• For equation: STATS → CALC → 0: Exponential function

Future value of investments for interest compounded continuously

S=Pe^rt

These are graphs that begin slowly, increase at rapid rate, slows over time at a rate of zero

What are Logistic functions

For logistic functions, what is the c term term referred to as?

The upper limit

Logistic Growth Functions

Logistic Decay Functions

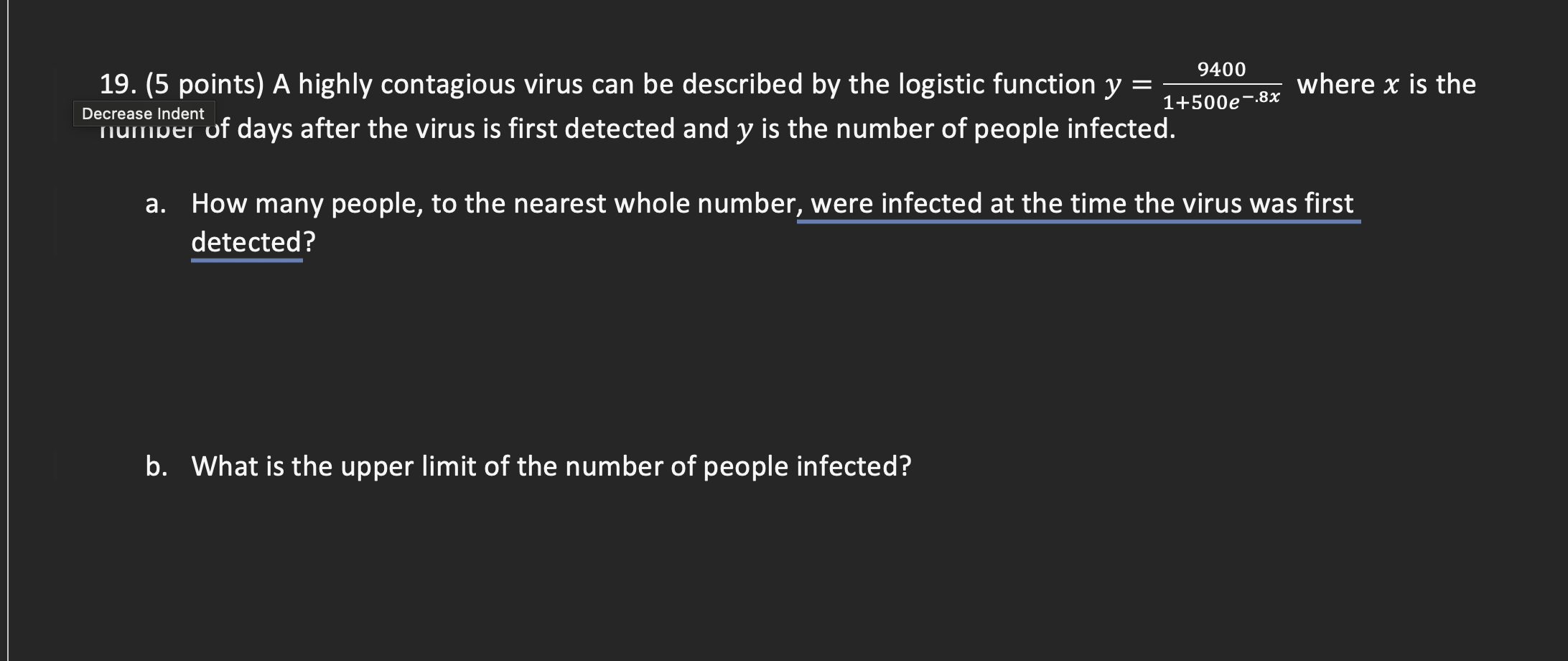
A) How many people, to the nearest whole number, were infected at the time the virus was first detected?

! Although it says first detected, x=0,

• 9400/1+500e^-0.8(0)= 19

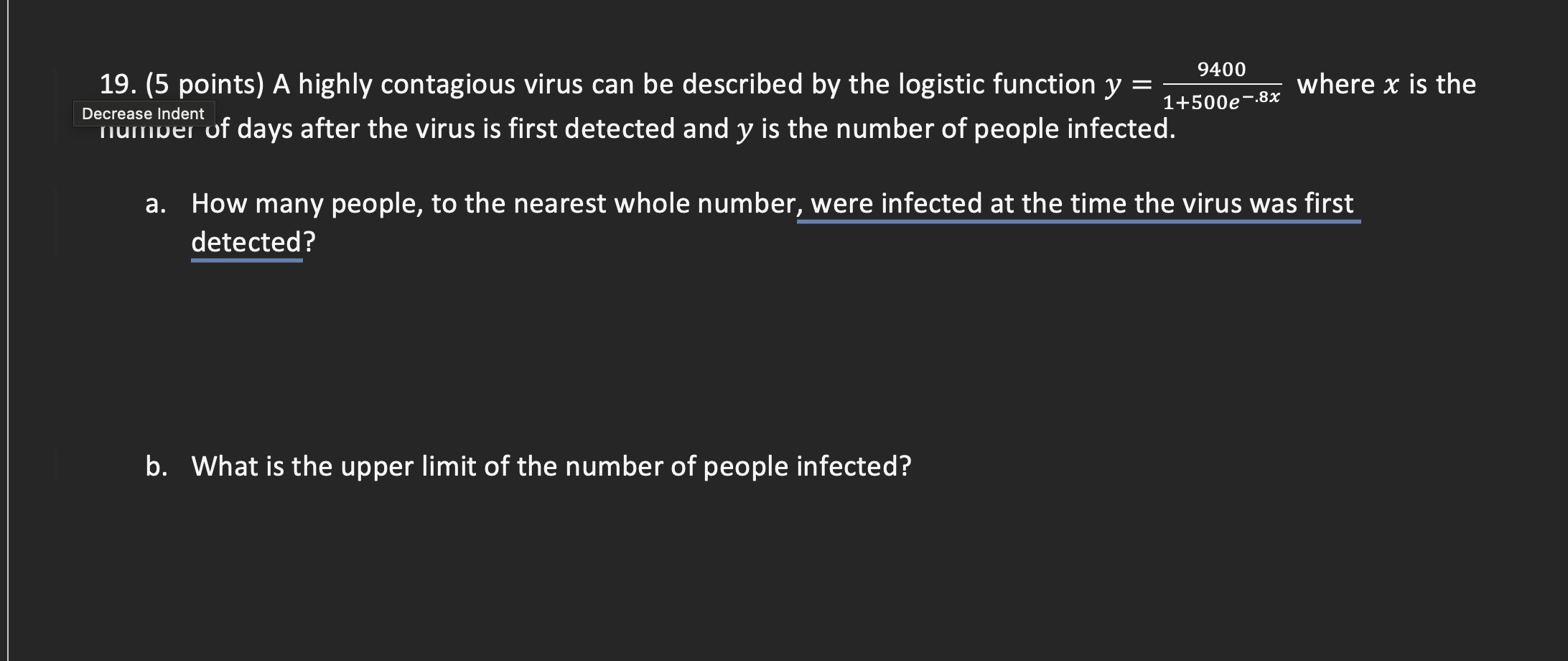
B) what is the upper limit?

C= upper limit, 9400.