Differential Equations

Differential Equation

Equation involving derivatives of a function. Usually solving one means solving for a function.

In this case The expression dw/dt literally means the change in weight with respect to time. Now the question says the rate of weight gain is inversely proportional to age which means as age goes up weight gain goes down

How do you verify the solution to a differential equation?

In order to verify a solution to a differential equation first find the derivative of your proposed solution then replace y or whatever the variable is in your given equation with your proposed solution. IF the derivative of your proposed solution matches the given equation with your solution subbed in as the appropriate variable(s) then your proposed solution is correct.

How does one use a slope field?

A slope field is a field used only for first order differential equations as a first order only has one input and output so it can be modeled in the xy plane. It is a brute force method in which we put the x and y values we want into the equation and then draw a slope representing the equation centered on the numbers we tested.

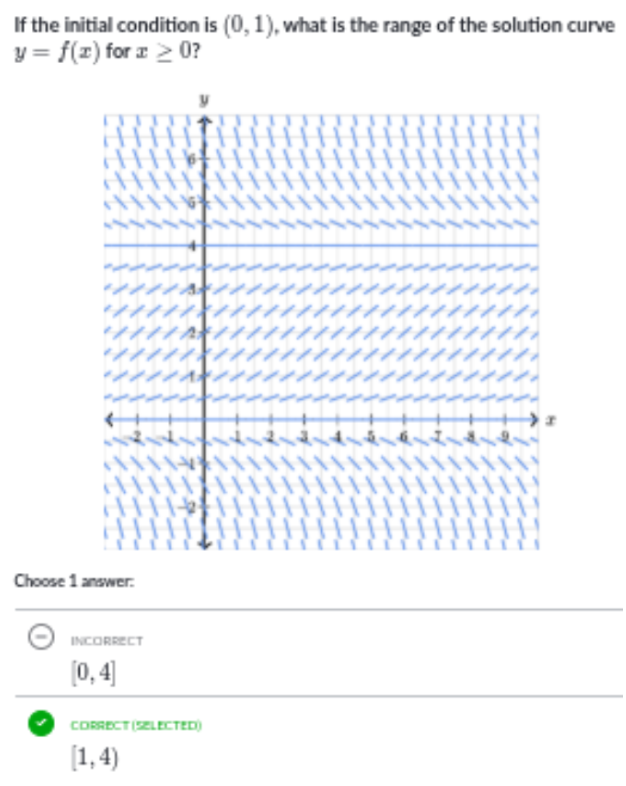
What is the solution curve to a differential equation given an initial condition?

The solution curve is the curve you can just make out that goes through a given area. In the case of an initial condition go to the indicated point and note its y value then follow the curve of the slope field until it ends. The y value from which the curve/initial condition starts to the one at which it ceases as you get a horizontal asymptote is called the solution curve.

How does one use eulers method?

Euler's method is a method for estimating a solution of a differential equation; it is an approximation. The smaller the step size the more accurate it is.

For these questions you will be given: the base function, a point, and a step size.

First make a table with the x value then y value then dy/dx. For the point you're given put the x coordinate in the x category and the y coordinate in the y category. Plug those x and y values into the given equation to get dy/dx. Note that dy/dx will be y for the next row and x for the next row will be x+the step size.Repeat for how many steps you'll need. To go backwards just do the above in reverse.

What is a seperable differential equation?

When you separate a differential equation you look at the part that says dy/dx and make dy one thing and dx the other then set them as equal to each other that way dy/dx will be the same ratio making everything equal and giving a function that acts as a solution. For an equation to be seperable it has to be of the form dy/dx=x*y

How does one solve a separable differential equation?

When doing differential equations via separation we treat dy and dx as a normal fraction (which works because math) and we try to separate the corresponding parts of the function. In the end this should give two functions one ending with dy and one ending with dx. After that we integrate setting the integrals equal to each other. When finished integrating add c to the part that was dx per convention then find c is possible after that just isolate for y and then y=something will be your solution.

How do you find the integral of a differential equation?

For these problems you'll be given a differential equation and the value of the integral at a point so all you have to do is find the antiderivative of the differential equation then solve it for the same x value as the given point which will give you some value. That value must be equal to the given value of the point so the difference in values between the value you got and the points value is c.

How does one isolate a variable from the original function and find it's value when given another variable value while only knowing another point ?

(keep in mind this says y(t)=2.

For these questions usually you'll have a differential equation (dy/dx) equal to some constant multiplied by a variable and asked to solve for y or t or x. Simply apply the idea of separation of variables. Separate the part containing the variable from the constant and integrate with respect to the variable. As usual the bottom of the equation will be the part you add c to. At this point oftentimes they'll give you the value of the integral at a point so with that you'll find c. Now plug in the value they want you to find the variable at into one side of the equation and then just solve the variable for the other side to keep it all equal.

How does one solve a differential equation of the form dy/dt =ky

Keep in mind t is a variable that should never be touched

How does one solve a differential equation of hte form k*f(x)

Keep in mid that one shouldn't touch x.

How do we model a situation where something is growing continuously when given an initial amount, secondary amount, and period?

Here isubv is the initial value. T is the growth rate given by ssubv (or secondary value) over isubv. P is the period. And e and x remain unchanged so as to represent that continuous growth.

How does one find the maximum of a quadratic?

With a quadratic the vertex will be perfectly centered between the two zeroes so you can just find the two points where the function is 0 then average those 2 points.