FTCE - Elementary Education K-6 - Math

A kindergarten class is learning about addition without regrouping. Which of the following strategies would be most appropriate to begin teaching students how to add two digits?

A. acting out addition by having students wear different colors

B. telling a story about a funny character who adds numbers

C. letting partners work in groups with leveled practice

D. using realistic examples in a familiar context

D. using realistic examples in a familiar context

The correct answer is D. using realistic examples in a familiar context because young children learn best when they can connect new concepts to real-life experiences. By presenting addition in a way that relates to their everyday lives, such as counting toys, snacks, or classroom objects, students can better grasp the meaning of combining numbers. While acting, storytelling, and group work can be helpful, using familiar, concrete examples provides the strongest foundation for understanding addition.

Simplify the expression.

90 − 60 ÷ 30 + 10

A. 10

B. 11

C. 78

D. 98

D. 98

The correct answer is D. 98 because following the order of operations, division comes first. Dividing sixty by thirty gives two. Subtracting two from ninety results in eighty-eight, and adding ten gives the final answer of ninety-eight.

Which of the following is NOT equivalent to 22/7?

A. 2 + 8/7

B. 1 + 15/7

C. 3(7/1) + 1/7

D. 3(7/7) + 1/7

C. 3(7/1) + 1/7

The correct answer is C. 3 times seven over one plus one over seven because it simplifies to twenty-one plus one over seven, which equals twenty-two over seven, not an incorrect representation. However, the fraction seven over one represents a whole number, and multiplying it by three results in twenty-one, which does not correctly follow the mixed number breakdown of twenty-two over seven in the same way as the others.

Simplify the following expression. 30 ÷ (7 − 2) × 2

A. 3

B. 6

C. 12

D. 24

C. 12

The correct answer is C. 12 because following the order of operations (parentheses, division, multiplication, addition, and subtraction), the first step is to solve the expression inside the parentheses, which is seven minus two, giving five. Then, dividing thirty by five results in six, and finally, multiplying by two gives twelve.

Kruti just purchased 3 shirts, 1 skirt, and 2 pairs of shoes. She would like to compute the change she would receive from a $100 bill. Which operation should she use last?

A. addition

B. division

C. multiplication

D. subtraction

D. subtraction

The correct answer is D. subtraction because after adding up the total cost of the items and possibly using multiplication to find the total price of multiple identical items, Kruti’s final step would be to subtract that total from the 100 dollars to determine how much change she will receive.

A teacher is explaining a mental mathematics strategy to the class and says:

Suppose we wanted to add 76 + 9. One way to do this addition problem is to think: 76 + 9 is the same as 76 plus 10 minus 1, because 10 minus 1 is 9. By adding 76 and 10, we get 86, then subtracting 1 gives the answer 85. This kind of thinking is also called "making 10."

What type of strategy is being taught?

A. compensation

B. partitioning

C. estimation

D. rounding

A. compensation

The correct answer is A. compensation because this strategy involves adjusting one number to make the calculation easier and then compensating for that adjustment. In this case, the teacher adds 10 instead of 9 (making the math simpler) and then subtracts 1 to balance the change. This method helps students perform mental math more efficiently by working with easier numbers.

Which of the following numbers represents 75 thousandths?

A. 0.0075

B. 0.075

C. 0.75

D. 7.50

B. 0.075

The correct answer is B. 0.075 because “seventy-five thousandths” means the number should be in the thousandths place, which is the third decimal place. The number 0.075 correctly represents this, as it is read as “seventy-five thousandths.” The other options either place the digits in the wrong decimal position or represent entirely different values.

A 4th-grade student is experiencing difficulty in understanding the concept of place value. Which of the following is the best strategy for reteaching the concept?

A. using counters and a chart to display numbers

B. reviewing the content of the textbook

C. providing a workbook for practice at home

D. repeating the previous lessons

A. using counters and a chart to display numbers

The correct answer is A. using counters and a chart to display numbers because place value is a foundational concept that is best understood through hands-on, visual learning. By using counters and a place value chart, the student can physically see how numbers are grouped into ones, tens, hundreds, and beyond, making the concept more concrete and easier to grasp. The other options focus on repetition and independent practice, which may not be as effective for a student struggling with understanding the concept in the first place.

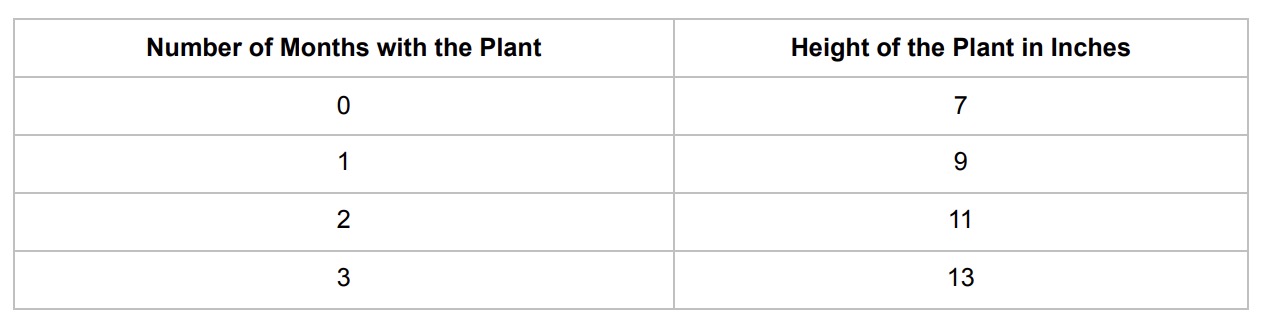
A student was responsible for taking care of a plant over a 3 month period. The student measured and recorded the height of the plant at the end of each month as shown in the table.

Which of the following equations relates the height of the plant, h, and the number of months, m, that the student had taken care of the plant, assuming a constant rate of growth?

A. 2h + 2 = m

B. 7m + 2 = h

C. 2m + 7 = m

D. 2m + 7 = h

D. 2m + 7 = h

The correct answer is D. Two times the number of months plus seven equals the height of the plant because the equation should show a steady increase in height over time, starting from an initial height. This equation means that the plant began at a height of seven units and grew by two units for each month the student took care of it. The other options do not correctly represent this relationship.

Which step should be done first to simplify the expression?

8a − 4a ÷ 2a − 16a • 8a + a

A. 8a − 4a

B. 8a + a

C. 4a ÷ 2a

D. 16a • 8a

C. 4a ÷ 2a

The correct answer is C. 4a ÷ 2a because, according to the order of operations (PEMDAS/BODMAS), division and multiplication must be performed before addition and subtraction. In the given expression, the division 4a ÷ 2a appears first in the order of operations, so it should be simplified before any addition or subtraction is done.

Which equation illustrates the associative property of multiplication?

A. (a • b)c = (b • a)c

B. (a • b)c = a(b • c)

C. (a + b)c = a • c + b • c

D. (a + b) + c = a + (b + c)

B. (a • b)c = a(b • c)

The correct answer is B. (a • b)c = a(b • c) because the associative property of multiplication states that the way numbers are grouped in multiplication does not change the product. This means that when multiplying three numbers, you can change the grouping with parentheses without affecting the result. Option B demonstrates this by showing that multiplying a and b first, then c gives the same result as multiplying b and c first, then a.

A group of students are working on a project. They complete 30% of the project in 12 hours. If they continue to work at the same speed, how many hours will it take the group to finish the project?

A. 24 hours

B. 36 hours

C. 40 hours

D. 42 hours

C. 40 hours

The correct answer is C. 40 hours because if the group completes 30% of the project in 12 hours, then we can determine how long it will take to complete 100% by setting up a proportion. Since 30% corresponds to 12 hours, each 1% takes 12 ÷ 30 = 0.4 hours. Multiplying by 100%, the total time needed is 0.4 × 100 = 40 hours, making option C the correct choice.

A teacher wants to build a scale model of the Earth and Pluto to compare their sizes. The Earth has a diameter of approximately 8000 miles and Pluto has a diameter of approximately 1500 miles. If the teacher builds a model of Earth with a diameter of 32 inches, what should be the diameter of her model of Pluto?

A. 5 1/3 inches

B. 6 inches

C. 6 3/2 inches

D. 8 inches

B. 6 inches

The correct answer is B. 6 inches because the teacher’s model of Earth scales down the real Earth’s diameter from 8000 miles to 32 inches. To keep the scale consistent, Pluto’s model must be scaled down using the same ratio. Since 8000 miles is reduced to 32 inches, the scale factor is 32 ÷ 8000 = 1/250. Applying this same factor to Pluto’s 1500-mile diameter, we get 1500 ÷ 250 = 6 inches, making option B the correct choice.

A teacher went to the store to buy treats for her classroom. At the store, she found the following deals. Which deal is the best buy?

A. 26 treats for 4 dollars

B. 48 treats for 8 dollars

C. 57 treats for 9 dollars

D. 100 treats for 16 dollars

A. 26 treats for 4 dollars

The correct answer is A. 26 treats for 4 dollars because to determine the best buy, you need to find which option has the lowest cost per treat. By dividing the total cost by the number of treats in each option, you find that option A gives you each treat for about 15.4 cents, while the other options cost slightly more per treat. Since option A provides the lowest cost per treat, it is the best deal.

An 8 foot square floor is to be covered with square tiles measuring 8 inches on each side. If each tile costs 50 cents, how much will it cost to tile the floor?

A. $32

B. $64

C. $72

D. $96

C. $72

To find the cost to tile the floor, first calculate the area of the floor in square inches (8 feet = 96 inches, so area = 96 x 96 = 9216 square inches). Each tile covers 64 square inches (8 inches x 8 inches), so you need 9216 / 64 = 144 tiles. At 50 cents each, the total cost is 144 x 0.50 = $72.

A living room is two times as long and one and one-half times as wide as a bedroom. The amount of carpet needed for the living room is how many times greater than the amount of carpet needed for the bedroom?

A. 1 1/2

B. 2

C. 3

D. 3 1/2

C. 3

The correct answer is C. 3 because the area of a rectangle is found by multiplying its length and width. If the living room is twice as long and 1.5 times as wide as the bedroom, its area is calculated as:

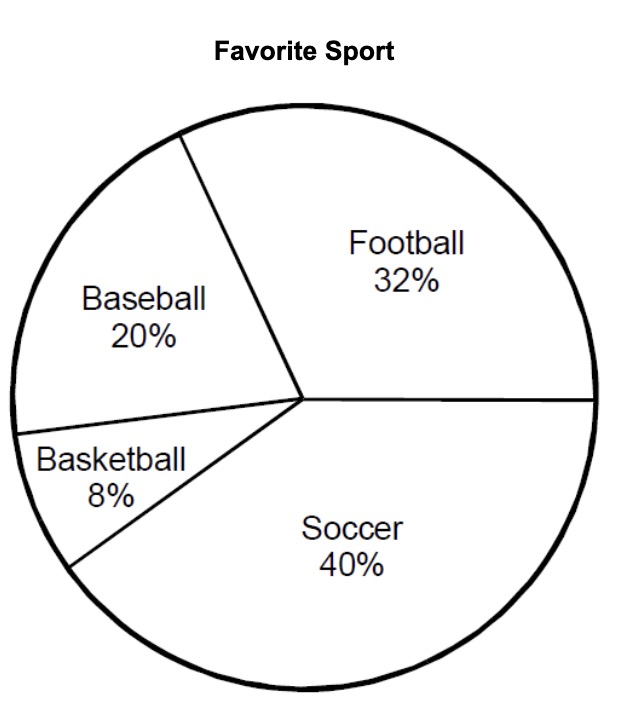
The following circle graph shows the results of a survey of 150 students. How many students chose baseball as their favorite sport?

A. 15

B. 20

C. 30

D. 40

C. 30

To determine how many students chose baseball as their favorite sport, refer to the circle graph which indicates that 20% students selected baseball. Since 10% of 150 is 15, 20% would be 30.

Estimate the mass of a slice of bread.

A. 25 g

B. 25 mg

C. 25 kg

D. 25 oz

A. 25 g

The correct answer is A. 25 g because grams are the appropriate unit for measuring the mass of a slice of bread, and 25 grams is a reasonable estimate, whereas milligrams are too light, kilograms are far too heavy, and ounces would be an unusual unit for mass in a metric-based estimation.

The math supervisor polled the teachers in the school district concerning which day of the week to hold a staff development workshop. The results showed that 20% of the teachers preferred Monday, 15% preferred Tuesday, 10% preferred Wednesday, 25% preferred Thursday, and 30% preferred Friday. To decide which day to hold the workshop, which statistic should the supervisor use?

A. mean

B. median

C. mode

D. range

C. mode

The correct answer is C. mode because the mode represents the most frequently chosen option in a data set, and since the goal is to select the most preferred day, the supervisor should choose the day with the highest percentage (Friday at 30%).

Estimate the weight (mass) of an adult female.

A. 55 g

B. 55 lb

C. 55 kg

D. 55 mg

C. 55 kg

The correct answer is C. 55 kg because kilograms are the appropriate metric unit for measuring the weight (mass) of an adult female, and 55 kg is a reasonable estimate, whereas grams and milligrams are too small, and 55 pounds is significantly lower than the average adult female weight.

A bottle of children's cough syrup would most likely have a capacity of

A. 8 pints.

B. 8 milliliters.

C. 8 grams.

D. 8 fluid ounces.

D. 8 fluid ounces.

The correct answer is D. 8 fluid ounces because liquid medicines like children’s cough syrup are typically measured in fluid ounces or milliliters. Eight pints would be far too much, eight milliliters would be too little for a full bottle, and grams measure weight rather than liquid capacity. A standard bottle of cough syrup is commonly around eight fluid ounces, making this the best choice.

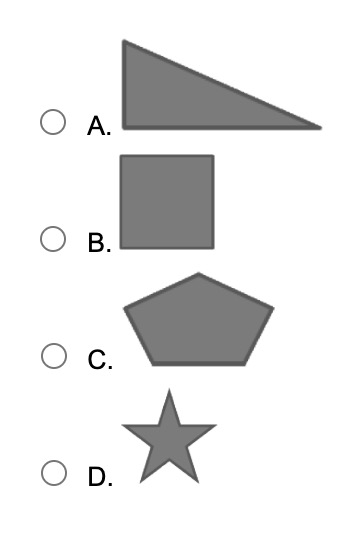
Which of the following polygons can be classified as regular?

B. Square

The correct answer is B, the square, because a regular polygon is defined as a shape in which all sides and angles are equal. Among the given options, the square is the only shape that meets this definition, as it has four equal sides and four equal angles. The triangle in option A appears to have sides of different lengths, making it irregular. The pentagon in option C does not have all sides and angles equal, so it is also irregular. The star in option D is not a regular polygon because its sides and angles vary. Since the square is the only shape with equal sides and angles, it is the correct choice.

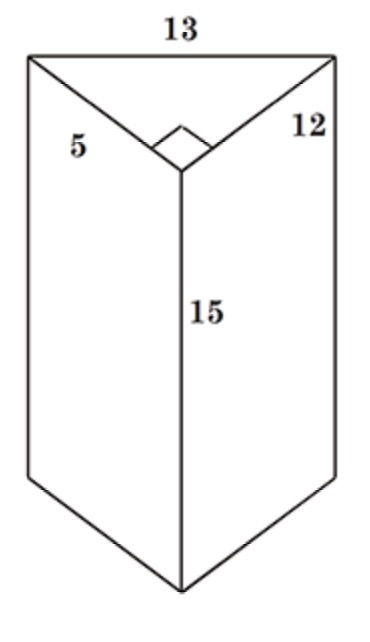
A right prism of height 15 cm has bases that are right triangles with legs 5 cm and 12 cm. Find the total surface area of the prism.

A. 315 cm²

B. 480 cm²

C. 510 cm²

D. 570 cm²

C. 510 cm²

The correct answer is C, 510 square centimeters, because the total surface area of the prism includes both triangular bases and the three rectangular lateral faces. The area of one triangular base is found using the formula for the area of a triangle, which is one-half times the base times the height. Since the triangle has legs of five centimeters and twelve centimeters, its area is one-half of five times twelve, which equals thirty square centimeters, and with two identical bases, their combined area is sixty square centimeters. The lateral surface area consists of three rectangles: the first has a width of five centimeters and a height of fifteen centimeters, giving it an area of seventy-five square centimeters, the second has a width of twelve centimeters and a height of fifteen centimeters, resulting in one hundred eighty square centimeters, and the third has a width equal to the hypotenuse of the triangular base, which is found using the Pythagorean theorem. The sum of five squared and twelve squared is twenty-five plus one hundred forty-four, which equals one hundred sixty-nine, and taking the square root gives thirteen centimeters for the hypotenuse, making the area of the third rectangle thirteen times fifteen, or one hundred ninety-five square centimeters. Adding the three lateral areas together, seventy-five plus one hundred eighty plus one hundred ninety-five equals four hundred fifty square centimeters, and adding that to the area of the two triangular bases, sixty plus four hundred fifty, results in a total surface area of five hundred ten square centimeters, making C the correct choice.

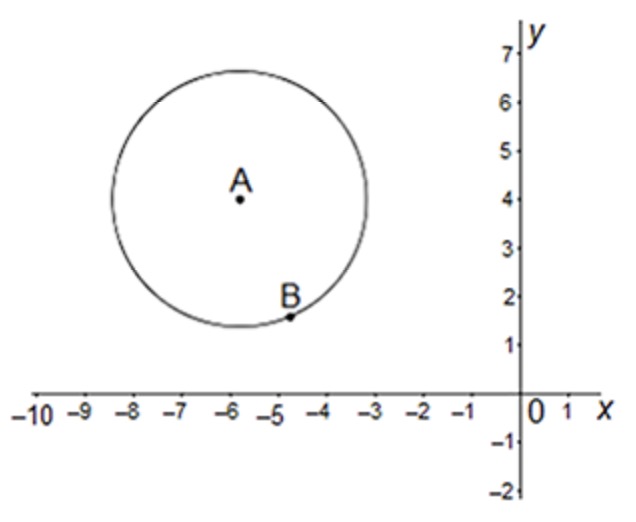
The center point of the circle is located at which point on the coordinate grid?

A. (4, 6)

B. (4, –6)

C. (–6, 4)

D. (6, –4)

C. (–6, 4)

The correct answer is C, (-6, 4) because the center of the circle is marked by point A on the coordinate grid. To determine its location, we identify its position by counting along the x-axis and y-axis. The center is aligned with -6 on the x-axis and 4 on the y-axis, meaning the coordinates are (-6, 4). The other answer choices either have the wrong sign or reverse the x- and y-values, making them incorrect.

A 6 th -grade teacher is plotting the vertices of a rectangle on a coordinate grid. The first 3 points he plots are (3, 1), (–1, 1) and (–1, –1). In what quadrant should the last vertex be plotted?

A. I

B. II

C. III

D. IV

D. IV

The correct answer is D, Quadrant IV, because a rectangle must have four vertices, and the fourth point should be placed to maintain its shape. The given points (3,1), (-1,1), and (-1,-1) form three corners of a rectangle. The first two points share the same y-coordinate, indicating a horizontal side, while the second and third points share the same x-coordinate, forming a vertical side. To complete the rectangle, the fourth point must align horizontally with (3,1) and vertically with (-1,-1), placing it at (3,-1). Since this point has a positive x-coordinate and a negative y-coordinate, it falls in Quadrant IV, making D the correct answer.

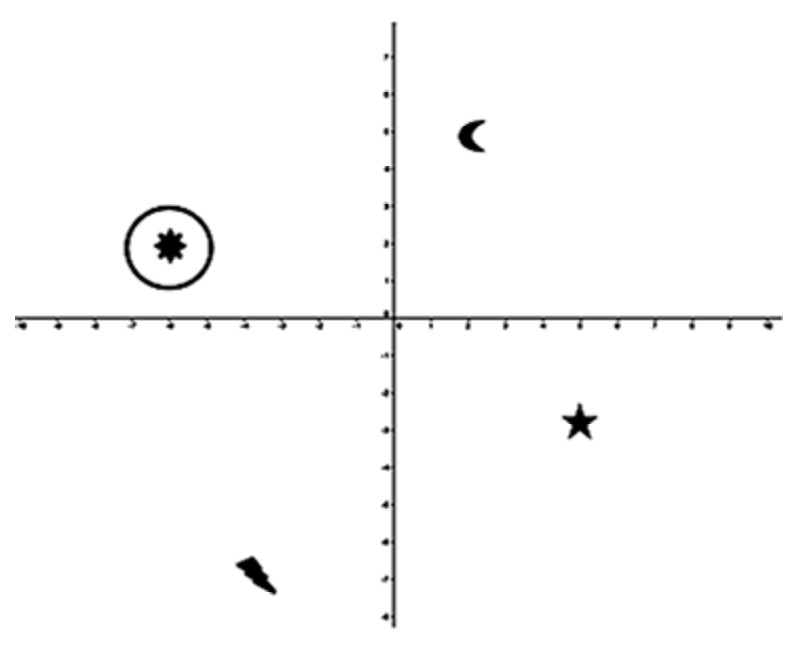
On an old map, a student circled the Sun. In which quadrant is the Sun located?

A. I

B. II

C. III

D. IV

B. II

The correct answer is B, Quadrant II, because the Sun is inside the circle drawn on the coordinate grid. Quadrant II is the section of the graph where x-values are negative and y-values are positive, meaning points in this quadrant are to the left of the y-axis and above the x-axis. Since the Sun is located in this region, it is correctly placed in Quadrant II, making B the correct choice.

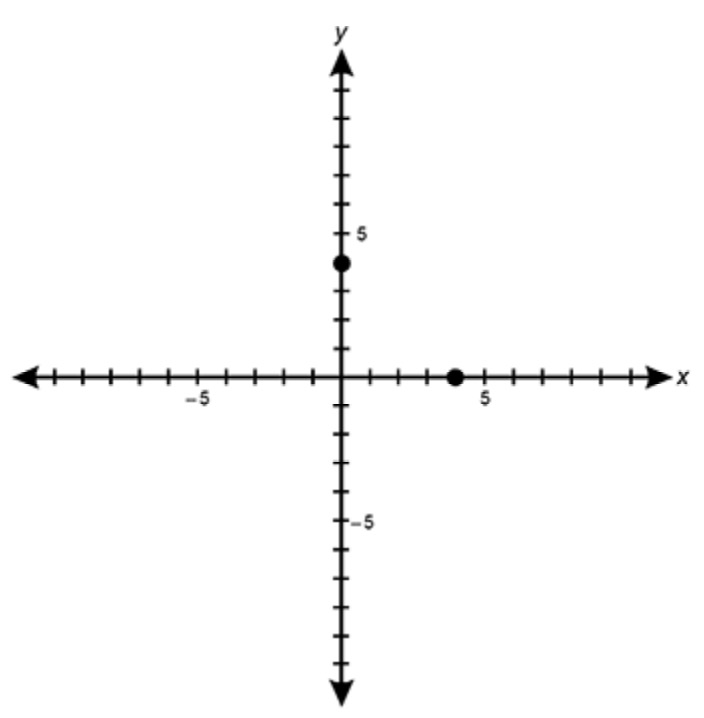
Two vertices of a triangle are plotted on the coordinate plane. Which of the following ordered pairs would result in the completed figure being a scalene triangle?

A. (0, 0)

B. (1, 1)

C. (2, –2)

D. (0, –4)

C. (2, –2)

The correct answer is C, (2, -2), because a scalene triangle is defined as a triangle in which all three sides have different lengths. The two given points on the graph are located at (0,5) and (5,0). To complete the triangle, we need a third point that ensures all three sides are of different lengths.

If we choose (2, -2) as the third point, the resulting triangle will have three distinct side lengths because the distances between (0,5), (5,0), and (2,-2) will all be different. The other options either create an isosceles triangle (where at least two sides are equal) or result in a degenerate triangle that does not form a proper shape. Therefore, C, (2, -2), is the correct choice as it ensures a scalene triangle.

Which statement is true about a triangular pyramid?

A. A triangular pyramid has 4 faces.

B. A triangular pyramid has 3 vertices.

C. A triangular pyramid has 7 edges.

D. A triangular pyramid has 1 square face.

A. A triangular pyramid has 4 faces.

The correct answer is A, a triangular pyramid has four faces, because a triangular pyramid, also known as a tetrahedron, consists of one triangular base and three triangular lateral faces, making a total of four faces.

Option B is incorrect because a triangular pyramid has four vertices, not three.

Option C is incorrect because a triangular pyramid has six edges, not seven.

Option D is incorrect because all faces of a triangular pyramid are triangles, meaning it does not have a square face.

Since a triangular pyramid always has four triangular faces, A is the correct choice.

A rectangular prism has a length of 3 units, width of 4 units, and a height of 5 units. What is the volume of this prism?

A. 15 units³

B. 20 units³

C. 60 units³

D. 94 units³

C. 60 units³

The correct answer is C, 60 cubic units, because the volume of a rectangular prism is found using the formula length times width times height. Given that the prism has a length of 3 units, a width of 4 units, and a height of 5 units, multiplying these values together gives 3 times 4 times 5, which equals 60 cubic units. The other answer choices do not correctly apply the volume formula, making C the correct choice.

Which of the following sequences is the most appropriate learning progression through the levels of geometric thinking?

A. analytic, abstract, descriptive

B. analytic, descriptive, abstract

C. descriptive, abstract, analytic

D. descriptive, analytic, abstract

D. descriptive, analytic, abstract

The correct answer is D, descriptive, analytic, abstract, because this sequence reflects the natural progression of geometric thinking as students develop their understanding of shapes and spatial relationships. At the descriptive level, students recognize shapes based on their appearance without analyzing their properties. As they advance to the analytic level, they begin identifying and comparing characteristics such as side lengths and angles, allowing for a more structured classification of shapes. Finally, at the abstract level, students use logical reasoning, theorems, and proofs to understand geometric concepts beyond just visual recognition. This ordered development aligns with how geometric reasoning typically evolves, making D the correct choice.

A local school district requires all 5th graders to complete an untimed test containing 50 multiple choice mathematics problems. The tests are scored and the results are compared throughout the district. What component of mathematics fluency is most likely the goal of this type of assessment?

A. rate

B. flexibility

C. automaticity

D. accuracy

D. accuracy

The correct answer is D, accuracy, because the assessment is untimed and focuses on solving 50 multiple-choice math problems, meaning the emphasis is on getting the correct answers rather than speed. If the goal were rate, the test would likely be timed to measure how quickly students can solve problems. If it were flexibility, the test would assess different strategies students use to solve problems rather than just their final answers. If it were automaticity, the focus would be on recalling basic math facts quickly without much effort. Since the purpose of this district-wide test is to measure correctness without time pressure, accuracy is the most relevant goal, making D the correct choice.

A student is struggling to progress through the descriptive level of geometric thinking. Which of the following skills is considered the most basic in the levels of geometric thinking?

A. recognizing and identifying shapes

B. understanding properties of shapes

C. perceiving characteristics of shapes

D. composing and decomposing shapes

A. recognizing and identifying shapes

The correct answer is A, recognizing and identifying shapes, because this is the most fundamental skill in geometric thinking and serves as the foundation for further development. At the descriptive level, students begin by simply recognizing and naming shapes based on their overall appearance, without yet analyzing their properties or relationships. Understanding properties of shapes, perceiving characteristics, and composing or decomposing shapes are more advanced skills that come later as students develop deeper spatial reasoning. Since recognizing and identifying shapes is the first step in geometric learning, A is the correct choice.

Students in the 3rd grade study multiplication in terms of equal groups, arrays, and area. What should students in the 4th grade be expected to do as the next step in this learning progression?

A. learn concepts, skills, and problem solving for multiplication and division

B. extend their concept of multiplication to make multiplicative comparisons

C. find whole number quotients and remainders involving two-digit divisors

D. apply their previous understanding of multiplication to multiply fractions

B. extend their concept of multiplication to make multiplicative comparisons

The correct answer is B, extend their concept of multiplication to make multiplicative comparisons, because the natural next step in the progression of multiplication learning from 3rd to 4th grade is understanding multiplication in terms of comparison rather than just repeated addition or grouping. In 3rd grade, students focus on multiplication as equal groups, arrays, and area models, laying the foundation for seeing multiplication as a way to describe “how many times larger” or “how many times more” one quantity is compared to another. In 4th grade, students typically learn to interpret statements such as “4 times as many” or “3 times as large,” which deepens their understanding of multiplication beyond basic computation. The other choices represent important skills but occur at different stages, such as learning basic multiplication and division in 3rd grade, working with division of larger numbers later in 4th or 5th grade, and multiplying fractions in later grades. Since making multiplicative comparisons is the appropriate next step in 4th grade, B is the correct answer.

Which of the following concepts is recommended to be taught first in the development of fractional understanding for students?

A. comparing sums of unit fractions

B. using set models to show fractions

C. adding fractions of unlike denominators

D. representing fractions with area models

D. representing fractions with area models

The correct answer is D, representing fractions with area models, because visualizing fractions using area models helps students build a strong foundational understanding of what fractions represent before moving on to more complex operations. Area models, such as shading parts of a shape to show fractions, allow students to see fractions as equal parts of a whole, which is essential for developing conceptual understanding. Comparing sums of unit fractions, using set models, and adding fractions with unlike denominators require a more advanced grasp of fractions. Since area models provide the most concrete and accessible introduction to fractions, D is the correct choice.

In a 4th-grade mathematics meeting, two teachers are discussing ways to teach multiplication. Teacher A believes the class should be taught the standard algorithm as the best way to solve a multiplication problem. Teacher B believes the students should explore various multiplication strategies and decide which strategy is best for each problem. What component of math fluency is Teacher B promoting?

A. rate

B. flexibility

C. automaticity

D. accuracy

B. flexibility

The correct answer is B, flexibility, because Teacher B is encouraging students to explore and choose different multiplication strategies based on the problem at hand. This approach promotes the ability to use various methods to solve problems, which is the essence of flexibility in mathematical thinking. Flexibility allows students to adapt their strategies, depending on the problem’s context, rather than relying solely on one fixed method like the standard algorithm. The other components—rate, automaticity, and accuracy—focus more on speed, quick recall, and correctness, whereas flexibility is about being versatile in problem-solving.