Engineering materials

Define crystallography

The science of atoms in solids

Give some information on Nobel prizes in crystallography

Over 25 Nobel prizes on this topic

W. H. Bragg & W. L. Bragg for X-ray work in 1915

Watson, Crick & Wilkins for DNA structure in 1962

Lattices

An infinite array of points (the lattice points) each surrounded by an identical environment

Crystal

Made up of regularly arranged atoms/molecules/ions in a pattern that repeats in multiple dimensions

The unit cell

The volume, mapped out by the vectors in a lattice

They will pack perfectly without empty space

The “right” one is the simplest, smallest one

Describe lattices in vector format

1D: R = ua

2D: R = ua + vb

3D: R = ua + vb +wc

Bravais lattices

An array of discrete points generated by translation operations described by vector operations

Cubic lattice

All sides are the same length

All angles are 90 degrees

Tetragonal lattice

2 of the 3 sides are the same length

All angles are 90 degrees

Orthorhombic lattice

All 3 sides are different lengths

All angles are 90 degrees

Monoclinic lattice

All 3 sides are different length

2 of the 3 angles are 90 degrees

Triclinic lattice

All 3 sides are different lengths

All 3 angles are different

Rhombohedral lattice

All 3 sides are the same length

All 3 angles are the same size but NOT 90 degrees

Hexagonal lattice

Lattice that forms a hexagon

Angles are 60, 90 and 120 degrees

Miller planes

Also called lattice planes

Defined as imaginary planes on which lattice points lie

(Might be good to practice these: they’re not hard but they could come up)

Packing efficiency

The ratio of occupied to unoccupied space in a certain area

Expressed as %

Octahedral hole

A hole that lies between two planar triangles of spheres

Tetrahedral hole

Formed by a planar triangle of touching spheres capped by a single sphere lying in between them

What are some assumptions made when calculating packaging efficiency?

-Ions are incompressible spheres

-Arrangement of Ancona about a cation is stable only of anions avoid contact

-coordination number is as large as possible

Give some info on ionic solids

Generally brittle

High melting points

Most soluble in polar solvents (e.g. water)

Typically form for combinations of elements with large electro negativity differences

Give some info on rock salt structure

4NaCl in unit cell

fcc lattice

octahedral coordination

Cation and anion sites are topologically identical

Give some info on Cesium Chloride

1CsCl in unit cell

Cubic coordination

Adoption by chlorides, bromides and iodides of larger cations

Many metal alloys have a similar structure type

Give some info on ZnS Zinc Blende

4ZnS in unit cell

Tetrahedral coordination

Cation and anion sites are topologically identical

Give some info on single crystals

Very few materials are single crystals

Some examples are silicon (for electronics) and nickel-based superalloys

Give some info on polycrystals

Most metals are polycrystalline

Each separate crystal is called a grain

These have grain boundaries separating the crystals

Stiffness

The resistance. Of a structure to elastic (recoverable) deformation

Stiffness = load/deflection

Units: N/m

Torsional stiffness

Stiffness that exists depending on loading

Stiffness = torque/Angular deflection

Hooke’s Law

Stress is proportional to strain

For simple tension:

Young’s modulus = stress/strain

Modulus

Mechanical property which measures resistance of a material to elastic deformation

The higher the modulus, the more stress is needed to create the same amount of strain

Low modulus materials deflect a lot when bent

High modulus materials deflect very little

What does modulus relate to?

Bonding strength in materials

Also determines natural vibration frequency

low modulus = low frequency

What are the 4 elastic constants in the linear elastic region?

Young’s modulus (E)

Shear modulus (G)

Bulk modulus (K)

Poisson’s ratio (v)

Poisson’s ratios

The change in length divided by original length

Gives a corresponding strain in the axial direction

(Differs from that along the length)

Young’s modulus

Elastic constant for tension

About double the shear modulus

Shear modulus

Elastic constant for shear

Has a relationship with Young’s modulus (v is Poisson’s ratio)

G = E/(2(1+v))

Bulk modulus

Elastic constant for shear

Has a relationship with Young’s modulus (v is Poisson’s ratio)

K = E/(3(1-2v))

Poisson’s ratio of rubber

0.5 for elastomers (rubber)

Thin-walled cylinders expend in radius with no length change only if v = 0.5

Bicycle tyres can be pumped up without getting tighter or looser

Isotropy

When the properties of a material do not depend on the direction in which they are being measured

E.g. glass, ceramics, polymers and metals

Anisotropy

Their properties are dependent upon which direction in the material they are being measured

Give some examples of anisotropic materials

Wood - stiffer along the grain than with it

Fibre-composites are stronger and stiffer parallel to the direction of fibres than perpendicular to them

Cohesive energy

atoms are held together by bonds that behave like springs

Cohesive energy is a measure of the strength of the bonds

What’s the difference between stress and strain?

They are not material properties - they describe a stimulus and response

Stress is applied to a material by loading it

Strain - a change of shape - is its response

What are te stages of selection strategy?

Translation

Screening

Ranking

Documentation

Selection strategy - translation

Translation of design requirements into a prescription for a material, identifying constraints and desired objective

Selection strategy - Screening

Selection out of all materials the fail to meet constraints decided in translation

Selection strategy - Ranking

Ranking of materials decided in screening by their ability to meet the objective

Selection strategy - Documentation

Documentation of candidates that top-ranked during screening, allowing them to be explored in depth

Material index

Objective measures of performance. Can be:

A single material property e.g. tensile strength

A material property group e.g. modulus/density

What 3 concepts are used in the selection procedure?

Performance indices, which isolate the combination of material properties

Materials selection charts

Shape factors: used to quantify the shape of a cross section of beam

What 3 things specify a performance index?

Functional requirements

Geometric parameters

Properties of the material

What can loading on a component usually be broken down into?

Normally some combination of axial tension or compression, bending and torsion

What does p = f(F, G, M) mean?

The equation that describes performance of an object

P = performance

F = functional requirements

G = geometric requirements

M = material properties

f = function of

What do you do if a design includes a single objective that can be limited by multiple constraints?

Each constraint must be evaluated independently

Each constraint is used to obtain a different performance index

How does shape matter in materials selection?

Can modify the resistance to elastic deformation through variation in second moment of area

Will only affect loading situations where I is involved, i.e. bending, torsion or buckling

Efficient shapes use the least material to achieve a given stiffness

Elastic recovery

If load is removed below the yield stress, material returns to original dimensions

Yielding and plastic deformation

Permanent change of shape

Non-recoverable

Metals usually fail by plastic deformation

Creep

Increase of strain at constant stress

Only important for metals at high temperatures

Important for polymers at all temperatures

Fracture

Cracking and separation into two or more parts

Wear

Local removal of material from surfaces in contact and under stress

Tensile testing

Destructive tests which use shaped specimens that concentrate stress in a known gauge length

The sample is put in a tester with one end fixed and the other attached to a moveable cross-head

Fatigue

Failure under repeated (cyclic) loading

Engineering stress

Force over original area

True stress

Force over instantaneous area

What’s the relationship between true stress and engineering stress?

Since original area > instantaneous area, true stress is equal too or larger than engineering stress

Give some info on mechanical failure of ceramics

Only brittle fracture occurs with ceramics

No/very little plastic deformation occurs

Why doesn’t plastic deformation occur in ceramics?

At room temperature most ceramics materials suffer fracture before the onset of plastic deformation

Give some info on dislocations movement in crystalline ceramics

Very difficult because of ionic bonding

Very few slip systems in which the dislocations can move

Covalent bonds are relatively strong and need to be broken

Give some info on dislocations movement in non-crystalline ceramics

Plastic deformation does not occur by dislocation motion - no regular atomic structure

Occurs by viscous flow instead

Viscosity of glasses is very high and they tend not to deform before failing

Types of failure in ceramics

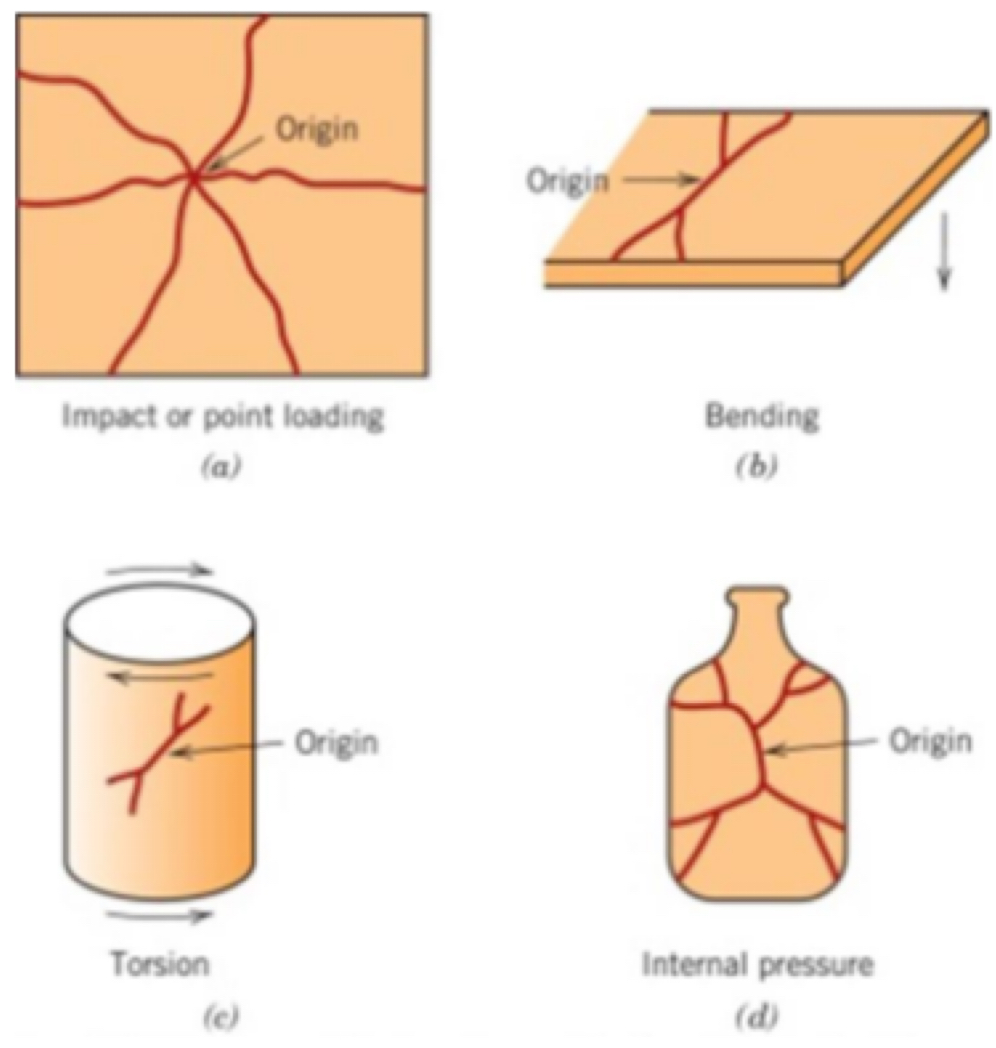
how strong are ceramics?

Ceramics are generally very tough/strong materials

Give some info on failure of ceramics

Ceramics fail because they have many surface flaws

Often, the ‘worst flaw’ propagates to failure

However, compressive failure can result by collapse of crush band of fragmented material

Why don’t we test ceramics in tension?

Difficult to prepare samples with required geometry

Difficult to grip samples without fracturing them

Ceramics show little/no plastic deformation before failing

How is tensile strength measured in ceramics?

Bend tests are used e.g. three-point

The top surface is in compression and the bottom surface is in tension

Please compare three and four-point bend tests

Four-point tests have constant bending moment between central supports

Three-point tests have high stresses at central loading point - can damage specimens

Are ceramics stronger in tension or compression?

Compression

Compressive strength = 10 x tensile strength

How do engineers use ceramics in practical applications?

Designs need to keep ceramics under compressive loading

E.g. reinforced concrete uses steel bars pre-stressed in tension to keep the surrounding concrete in compression

Which is more likely to break: a clay pot or a coffee mug?

The clay pot

Coffee mugs are normally glazed and therefore less porous

Give some info on mechanical failure of polymers

Polymers are similar to metals in that they can fail through fracture or plastic deformation

This is dependent on the polymer

Give some info on mechanical properties of polymers

Fracture strengths of polymers - 10% of those for metals

Deformation strains for polymers > 1000%

For most metals, deformation strains < 10%

Give some info on a non-cross linked polymer structure

No regular repeating pattern of polymer chains

Results in a glassy or amorphous structure

Give some info on a partly crystalline polymer structure

Regions in which polymer chains line and and register

Forms crystalline patches

Give some info on a slightly cross-linked polymer structure

Occasional cross-linking allowing the polymer to stretch

Typical of elastomers

Give some info on a heavily cross-linked polymer structure

Heavily cross-linked polymers exhibit chain sliding

Typical of epoxy

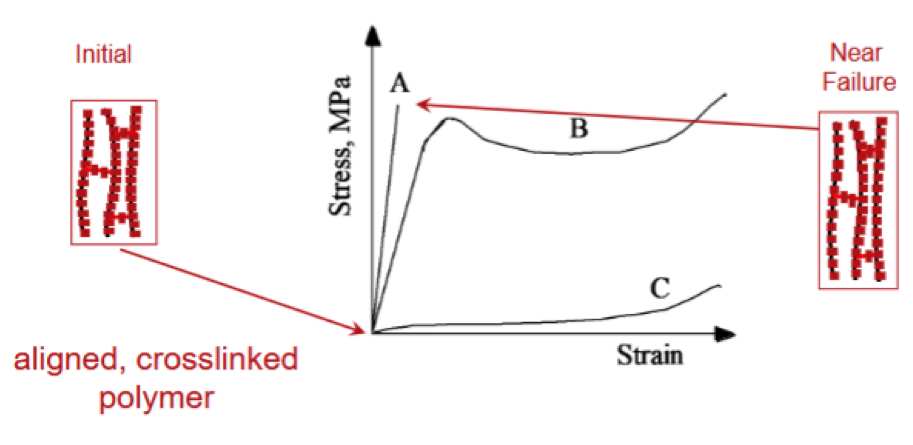
Give some info on the different polymers shown on this stress-strain curve

Polymer A is a brittle and is either heavily cross-linked or networked polymer

Only allows elastic deformation before failure

Only polymer B shows any significant plastic deformation

Give some info on the effect of temperature on tensile strength

As temperature increases the strength of most materials decreases

Strength decrease with temperature depends on material and temperature change

Polymers typically are very temperature sensitive

How does temperature increase effect temperature strength in polymers?

-decrease in the elastic modulus

-a reduction in tensile strength

-an increase in ductility

How are polymers normally strengthened?

Dislocations do not play a role in the strength of non-crystalline solids

Strengthening polymers can be done through blending, drawing, cross-linking, and by reinforcement

How does plastic deformation occur?

When large numbers of dislocations move and multiply

Results in macroscopic deformation

If we want to increase yield and tensile strength of a material, what do we do?

We need to introduce a mechanism which prohibits the mobility of these dislocations

Crystalline imperfections

Defects in metals and ceramics which prevent materials from achieving their ideal strength

Name some common examples of crystalline imperfections

Vacancies

Dislocations

Grain boundaries

Solute atoms on interstitial and substitutional sites

Dislocation

An extra half-plane of atoms in the crystal

Dislocations distort the lattice and make metals soft and ductile

Grain boundaries

Formed when different oriented crystals meet

The individual crystals are called grains, the meeting surfaces are grain boundaries

Made by cutting, slipping and rejoining bonds across a slip plane

Why is grain size important?

The size of the grains of our material can have an influence on the strength of the material

Typically, the smaller th egrain size the stronger the material

Grain

An individual crystal in a polycrystalline metal or ceramic

Grain boundary

The interface separating two adjoining grains with different crystallographic orientations

Grain size

The average grain diameter as determined from a random cross section

Oi, give us the Hall-Petch equation

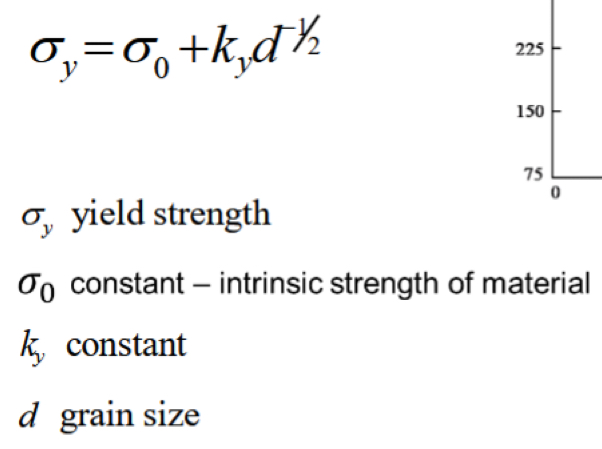
How can we control grain size?

Control during processing (casting, rolling, extrusion, heat treatment)

What are the different types of solid solutions?