(8) Linear Kinematics

Kinematic quantities

• Linear Position

• Linear Distance and Displacement

• Linear speed and velocity

  • average vs instantaneous

• Linear acceleration

Vector and Scalar

• Tip to tail method (adding multiple vectors)

• Vector Resolution and Composition (how to utilize vectors)

• Component method

Linear Position

• Linear location of object of interest at a given instant

• Vector: Magnitude + Direction

• Coordinates: r= [x, y] (r is the position vector)

• Unit: m (meter)

Linear Distance

• length of the path

  • how long/far

• Scalar: Magnitude only

• Unit: M

Linear Displacement

• change in linear position

  • net effect of motion

• Vector

• Unit: m

d= delta r= r₂ — r₁ = [x₂ - x₁, y₂ - y₁]

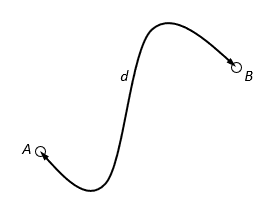
Tip to tail method- Purpose

• used in vector ADDITION

• to find the resultant(sum/net)

tip to tail- procedure

• connect all vectors tip to tail

• resultant(sum or net): the vector from the tail of the first vector to the tip of the last vector

• connection sequence is not important

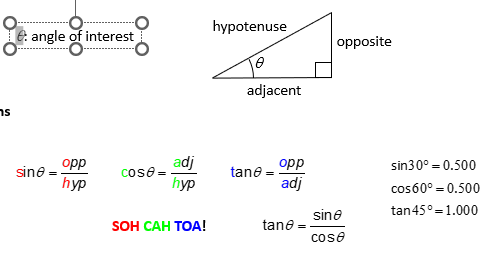
Basic Trigonometric functions

• Right triangle- hypotenuse, opposite leg, adjacent leg, theta is the angle of interest

• Basic trig functions

  • sine (theta)= opposite/hypotenuse

  • cosine(theta)= adjacent/hypotenuse

  • tangent(theta)= opposite/adjacent or sin/cos

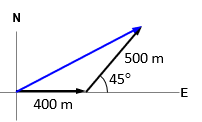
Vector resolution (decomposition)

Breaking down a vector into components

• v=v_x+v_y

• use hypotenuse and angle to find length of opposite and adjacent legs

• adj=hyp*cos(angle)

• opp=hyp*sin(angle)

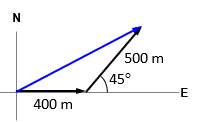
Vector Composition

composing a vector from components

• v=v_x+v_y

• use adj and opp to find hyp and angle

  • use Pythagorean theorem to find hyp

  • use arctan(opp/adj) to find theta

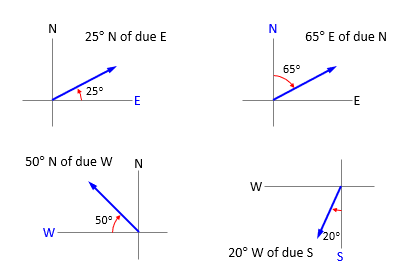
Directions relative to the cardinal directions

Reminder- the direction after Due is the side it starts on