Holding space for defying gravity

An object can be regarded as point mass when:

A body covers a very large distance as compared to its size, so, to study its motion, its size or dimensions can be neglected

Radial fields are considered _____ fields

non-uniform

What does this therefore mean?

g is different depending on how far object is from centre of mass of sphere

Gravitational are attractive and repulsive: T or F

Attractive only

What do gravitational field lines represent?

gravitational field

also direction of acceleration of test mass in field

Gravitational field lines around a point mass are ____ _____

radially inwards

equation for radial field strength:

g=-GM/r²

magnitude of g is plotted against the distance from the centre of a planet:

• r < R (the radius of the planet), g is directly proportional to r

• When r > R, g is inversely proportional to r² 

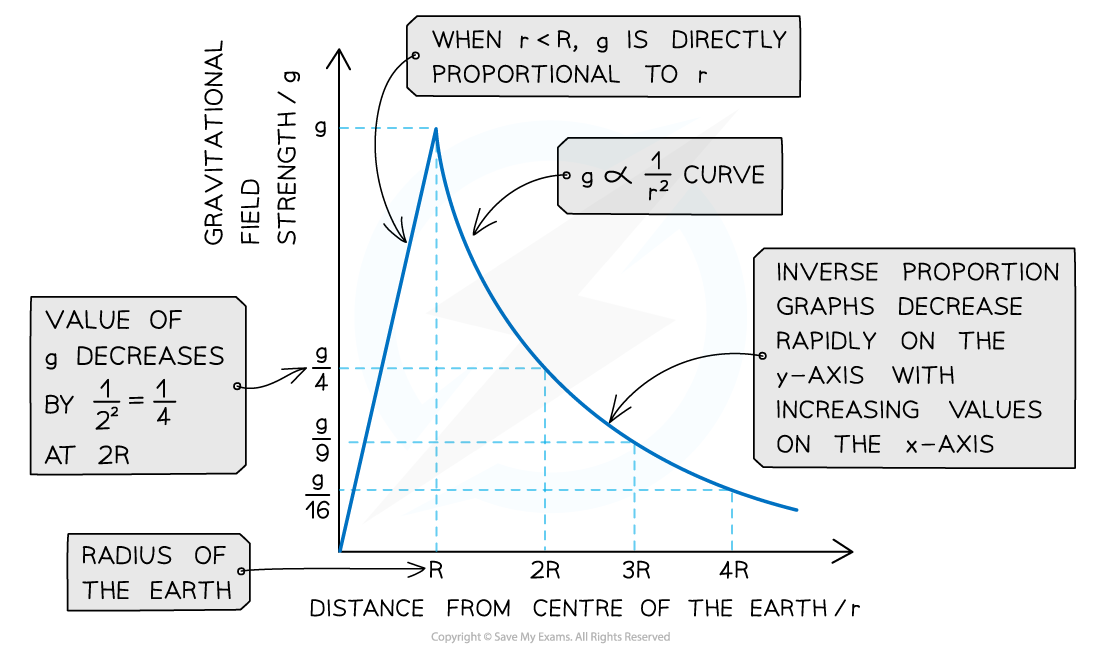
Near the Earth's surface, the gravitational field is ____

uniform

Newton’s Law of Gravitation states:

The gravitational force F between two masses m₁ and m₂ is proportional to the product of their masses and inversely proportional to the square of their separation, r

negative sign indicates what in newtons law of gravitation states?

that the gravitational force F between the two point masses m1 and m2 is attractive

radius of earth

6400km

What is Kepler’s first law?

The orbit of a planet is an ellipse, with the sun at one the two foci

Kepler’s second law:

A line segment joining the sun to a planet sweeps out equal areas in equal time intervals

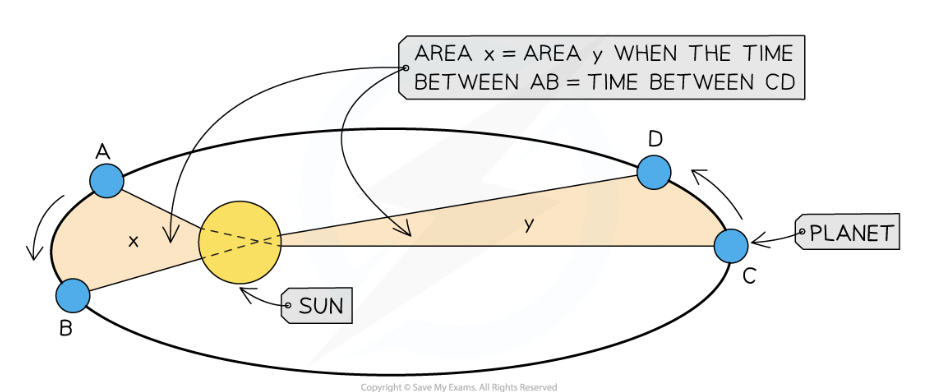
What does this therefore mean?

Planets closer to the sun travel faster and further away travel slower

Keplers 3rd law

Square of orbital time period T is directly proportional to cube of orbital radius r

How do we say planets move?

In circular motion

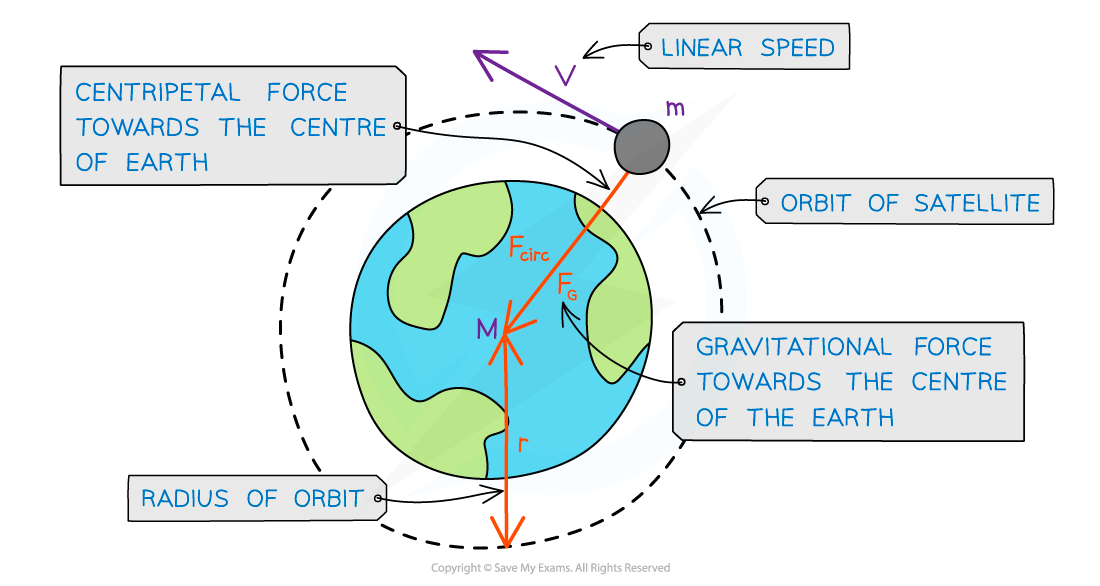
gravitational force is centripetal, so it is perpendicular to the direction of travel of the planet

gravitational force F on the satellite is centripetal

F=F_centripetal

How to find orbital speed?

GMm/r² = mv²/r

What does this therefore mean?

all satellites, whatever their mass, will travel at the same speed v in a particular orbit radius r

equation for speed of orbiting planet

v=2πr/ T

How to derive T²=4PI²r³/ GM

V=2 PI r/ T

V²=GM/r ( GMm/r²=mv²/r )

specific type of orbit in which the geostationary orbit satellite

• Remains directly above the equator

• Is in the plane of the equator

• Always orbits at the same point above the Earth’s surface

• Moves from west to east (same direction as the Earth spins)

• Has an orbital time period equal to Earth’s rotational period of 24 hours

What are geostationary satellites used for?

telecommunication transmissions (e.g. radio) and television broadcast

How do geostationary satellites works?

• A base station on Earth sends the TV signal up to the satellite where it is amplified and broadcast back to the ground to the desired locations

• The satellite receiver dishes on the surface must point towards the same point in the sky

  • Since the geostationary orbits of the satellites are fixed, the receiver dishes can be fixed too

Gravitational potential near surface of earth:

G.P.E = mgΔh

• When using this equation, the G.P.E on the surface of the Earth is taken to be zero

  • This means work is done to lift the object

Why can GPE= mgh only be used when objects are near earths surface?

This is because, near Earth's surface, the gravitational field is approximated to be uniform

Far away from the Earth's surface, the gravitational field is radial because the Earth is a sphere

In a radial field what is GPE defined as:

energy an object possesses due to its position in a gravitational field

Definition of gravitational potential at a point:

gravitational potential energy per unit of mass for an object at that point

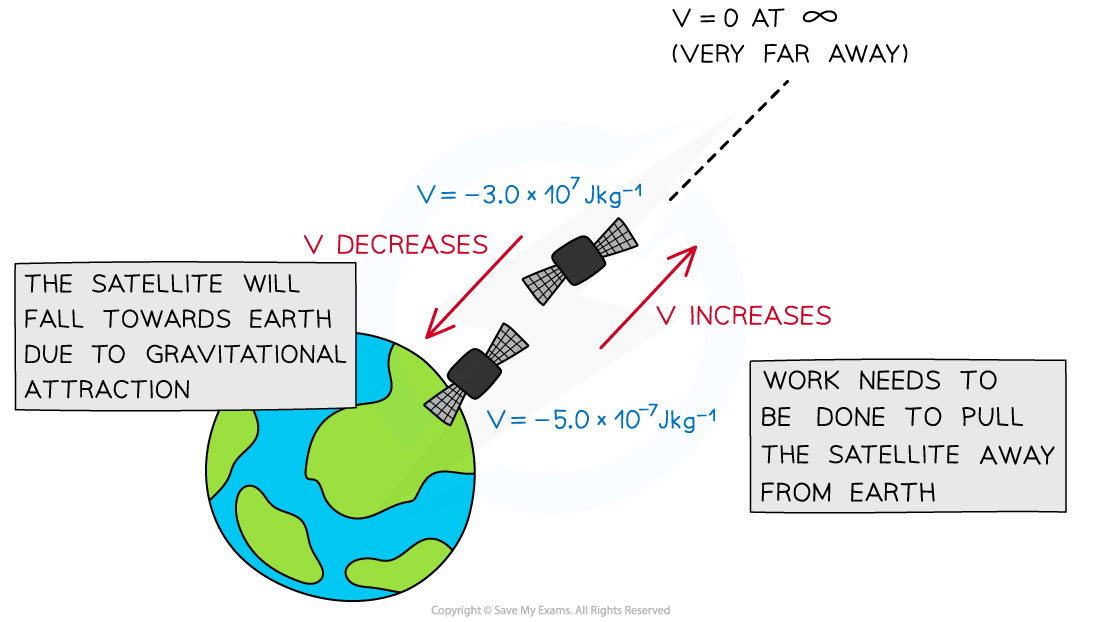
Gravity is always attractive, so work must be done on a mass to move it away to a point infinitely far away from every other mass

Why is gravitational energy always attractive?

• 'Infinity' is the point at which the gravitational potential is zero

• Therefore, since the potential energy of all masses increases as work is done on them to move them infinitely far away, the value of the potential is always negative

• Since the potential energy of a mass therefore increases as it moves toward infinity (where V = 0), the value of the potential everywhere else must be negative. 

Gravitational potential definition:

The work done per unit of mass in bringing a mass from infinity to a defined point

What does area of gravitational force against distance from planet equal?

work done

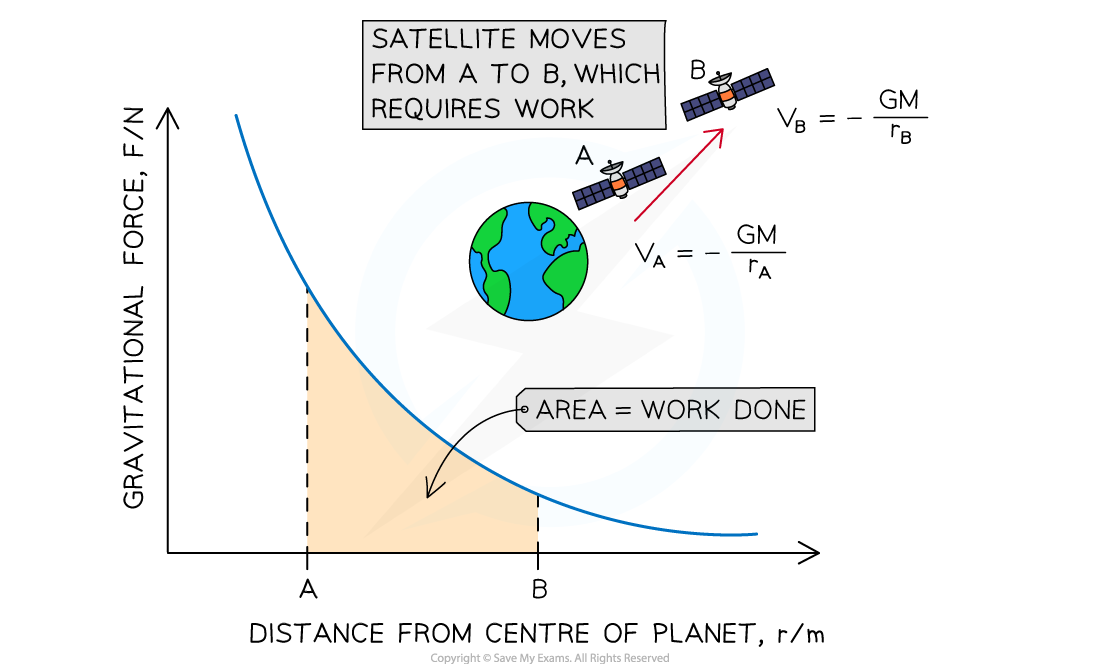
• In the case of a mass m moving further away from a mass M, the potential increases

• Since gravity is attractive, this requires work to be done on the mass m

• The area between two points under the force-distance curve therefore gives the change in gravitational potential energy of mass m

• When a mass is moved against the force of gravity, work is required

  • This is because gravity is attractive, therefore, energy is needed to work against this attractive force

Equation for change in GPE:

M = mass that is producing the gravitational field (e.g., a planet) (kg)

m = mass that is moving in the gravitational field (e.g., a satellite) (kg)

r1 = initial distance of m from the centre of M (m)

r2 = final distance of m from the centre of M (m)

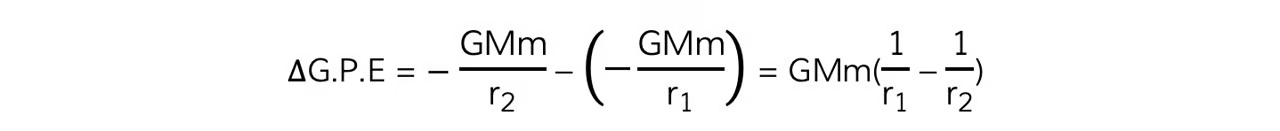
escape velocity definition:

The minimum speed that will allow an object to escape a gravitational field with no further energy input

escape velocity is ____ for all masses in same gravitational field

same

What needs to be transferred when object reaches escape velocity and what equation does this make?

KE —> gravitational potential energy

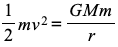
Units of equation

• m = mass of the object in the gravitational field of mass M (kg)

• v = escape velocity of the object (m s^-1)

• G = Newton's Gravitational Constant

• M = mass of the object to be escaped from, causing the gravitational field (i.e., a planet) (kg)

• r = distance from the centre of mass of M (m)

Why do rockets launched from earth’s surface not need to achieve escape velocity to teach orbit around earth?

• They are given energy through fuel continuously to provide thrust

• Less energy is needed to achieve orbit than to escape from Earth's gravitational field

UNITS OF VG

J KG^-1