calculus 2 trig identities & integrals

substitute cos(2x) with

cos²x-sin²x

substitute sinxcosx with

½sin(2x)

substitute sin(2x) with

2sinxcosx

substitute sin²x with (name both)

½(1-cos(2x))

1-cos²x

substitute cos²x with (name both)

½(1+cos(2x))

1-sin²x

Strategy for integrating even powers of sin and cos

Use half angle identities

sin²x = ½(1 − cos(2x))

cos²x = ½(1 + cos(2x))

sin(2x) = 2sinxcosx

Strategy for even powers of sec

1.) Factor out a sec²x.

2.) Replace the remaining even powers of secant using sec²x = 1 + tan²x

3.) Let u = tanx and integrate.

Strategy for odd powers of sin

1.) Factor out one power of sine.

2.) Replace the remaining even powers of sine using sin²x = 1 − cos²x

3.) Let u = cosx and integrate.

Strategy for odd powers of cos

1.) Factor out one power of cosine.

2.) Replace the remaining even powers of sine using cos²x = 1 − sin²x

3.) Let u = sinx and integrate.

Strategy for odd powers of tan

1.) Factor out a secxtanx.

2.) Replace the remaining powers of tangent using tan²x = sec²x − 1

3.) Let u = secx and integrate.

∫b^x

b^x/lnb

∫secx dx

ln|secx+tanx|+C

∫cscx dx

ln|cscx-cotx|+C

∫tanx dx

ln|secx|+C

∫cotx dx

ln|sinx|+C

∫csc²x dx

-cotx + C

graph of sinx

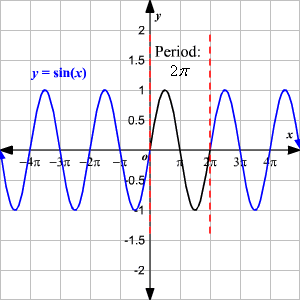
graph of cosx

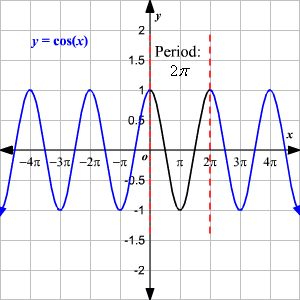
graph of tanx