Binary Search Tree Theory

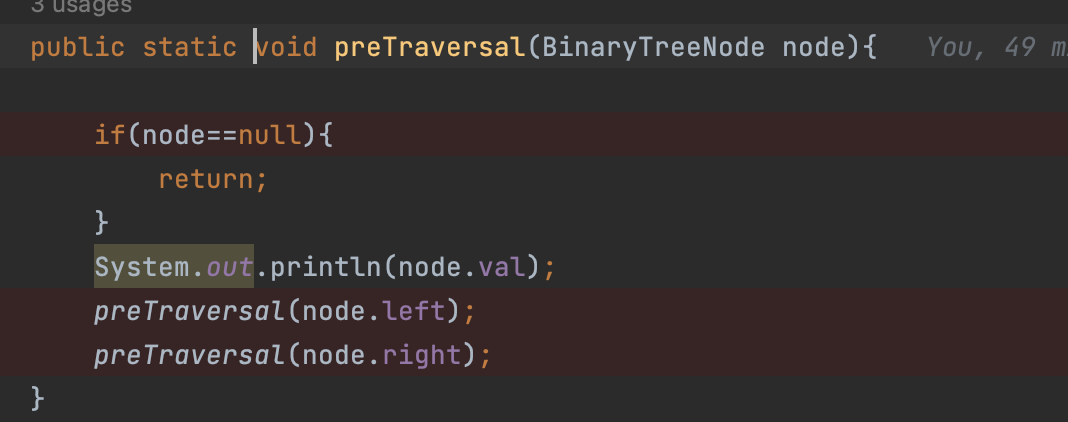
Binary Traversal - Preorder traversal

• visit root

• traverse left subtree in preorder

• traverse right subtree in preorder

Build Binary Tree

public class BinaryTreeNode{

int val ;

BinaryTreeNode left ;

BinaryTreeNode right;

}

Post Order Traversal

• Traverse the left subtree in Postorder.

• Traverse the right subtree in Postorder.

• Visit the root.

In order traversal

• Traverse the left subtree in Inorder.

• Visit the root.

• Traverse the right subtree in Inorder.

Properties of Binary Tree : give h as a height of a binary tree

What is number of maximun node in a full binary tree ?

The maximum number of nodes in a binary tree of height h is 2^(h+1) - 1.

Properties of Binary Tree : give h as a height of a binary tree

What is number of maximun node in a complete binary tree ?

Its range from 2^h → 2^(h+1) -1

Properties of Binary Tree : give h as a height of a binary tree

What is number of leaf node in a full binary tree

2^h

Properties of Binary Tree : give h as a height of a binary tree

What is number of NULL links (wasted pointers ) in a complete binary tree of n nodes

n+1

Basic Operations of full binary tree

• insert element into a tree

• delete element from a tree

• searching an element from tree

• traversing tree

Auxilliary Operations of Binary Tree

• find size of tree

• find height of tree

• find level which has maximun sum

• find LCA

Application of Binary Tree

• Expression trees are used in compilers.

• Huffman coding trees that are used in data compression algorithms.

• Binary Search Tree (BST), which supports search, insertion and deletion on a

  collection of items in O(logn) (average).

• Priority Queue (PQ), which supports search and deletion of minimum (or maximum)

  on a collection of items in logarithmic time (in worst case).

Tree Traversal Ways

1. DLR ( Preorder)

2. LDR (Inorder)

3. LRD (post order)

4. Level Order Traveral (go through each level)

Level Order Traversal

• Visit the root.

• While traversing level (, keep all the elements at level ( + 1 in queue.

• Go to the next level and visit all the nodes at that level.

• Repeat this until all levels are completed.

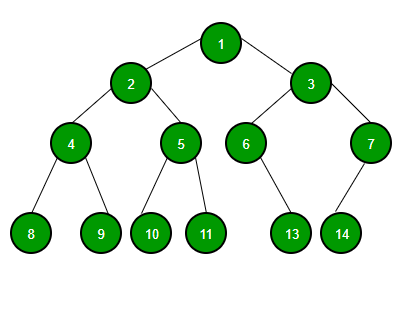
Given a tree , return value In order traversal