Mechanical (Work and Energy)

MEE1008: Dynamic Systems - Lecture 16

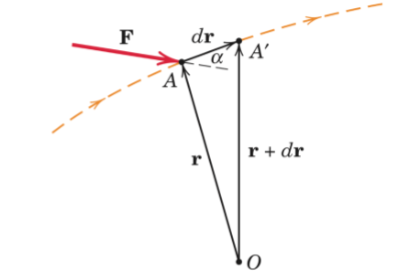
Work

dU = F.dr

= F.ds.cosα = F_t.ds

where α is the angle between F and dr, ds is the magnitude of dr and F_t is the component of the force in the tangential direction or in the direction of dr.

Work unit

Newton metre (Nm)

Joule (J)

Joule

The work done by a force of 1N acting through a distance of 1m in the direction of the force.

Calculation of work

U = ∫ F_t ds, within the limits s₁ and s₂.

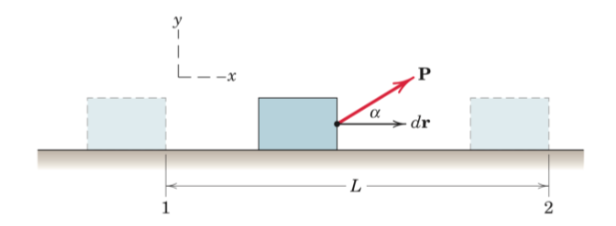
Work associated with a constant external force P.

U_1-2 = PcosαL

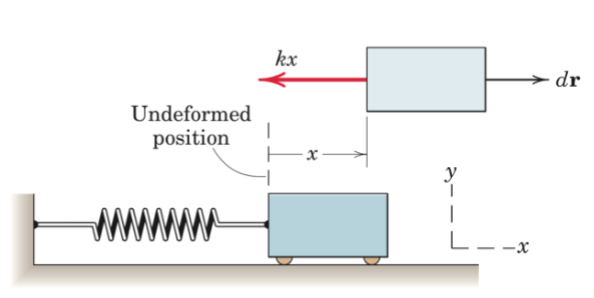
Work associated with a spring force

-½k(x₂² - x₁²)

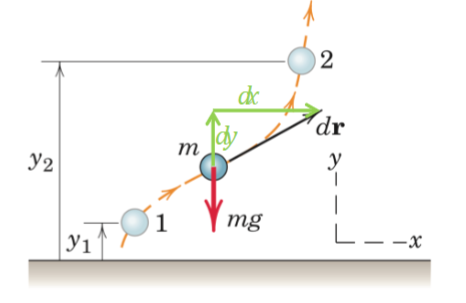
Work associated with weight (assumed constant g)

-mg(y₂ - y₁)

Kinetic energy of a particle

T = ½mv²

Work-energy equation for a particle

U_1-2 = ½m(v₂² - v₁²) = T₂ - T₁ = ΔT

Work always results in a change in energy.

Useful for solving problems that involve force, velocity and displacement.

Gravitational potential energy V_g

The work mgh done against the gravitational field to elevate the particle a distance h above some arbitrary reference plane (datum).

V_g = mgh

Elastic potential energy V_e

The work which is done on the spring to deform it is stored in the spring.

V_e = ½kx²

U’_1-2

The work of all external forces other than gravitational forces and spring forces.

T₁ + V₁ + U’_1-2 = T₂ + V₂

The kinetic energy at point 1 plus the potential energy at point 1 plus the work done between point 1 and point 2 is equal to the kinetic energy and potential energy at point 2.