Leaving Cert Maths Statistics Terms

An entire collection of individuals about which we want to draw conclusions

Population

The collection of information from the whole population

Census

A subset of the population (should be chosen at random to prevent bias)

Sample

The collection of information from a sample

Survey

Information about individuals in a population

Data

A quantity calculated from data gathered from a sample

Statistic

The pattern of variation of data

Distribtion

Data values that do not fit the pattern of the rest of the data

Outliers

Data that consists of non numeric information

Categorical Data

Ordinal & Nominal

Ordinal - can be ordered

Nominal - cannot be ordered

Two types of categorical data

Discrete & Continuous

Discrete - countable values

Continuous - data that can assume any value within a specified range

Two types of numerical data

A sample in which every member of the population has an equal chance of selection

Simple Random Sample

Where the population is split based on certain factors. EG age, sex

Stratified Sample

Where the population is divided into groups in terms of age, general education levels, social class etc.

The interviewer is then told how many people (the quota) to interview in each of these groups, but the interviewer make the choice of who exactly is asked.

- Disadvantage: the actual people or items chosen are left to the discretion of the interviewer which could lead to bias

Quota Sampling

A procedure in which the selected sampling units are spaced regularly throughout the population; that is, every n'th unit is selected.

systematic sampling

1. Pie charts

2. Bar charts

3. Steam and Leaf plots

4. Dot Plots

5. Line Pots

6. Histograms

Ways to represent data

A probability sampling technique in which clusters of participants within the population of interest are selected at random, followed by data collection from all individuals in each cluster. Not expensive.

cluster sampling

using a sample of people who are readily available to participate and easy for the tester. Eg. Taking the first forty names on the school register.

convenience sampling

-choosing a sample which is not representative (Karen is doing a survey on peoples attitudes towards a gambling. If she stands outside the casino and questions people as they enter or leave, the results will be biased as these people are ready involved in gambling)

- not identifying the correct population (example the school principal wants to find out about students attitudes to school uniforms she questions 10 leaving cert students only this may lead to biased results as opinions of the younger students first fifth years are not included)

- failure to respond to a survey (many people do not feeling responses to questionnaires sent through the post. Those who do respond may not be representative of the population being serve it)

- Dishonest answers to questions

Four examples of bias in sampling

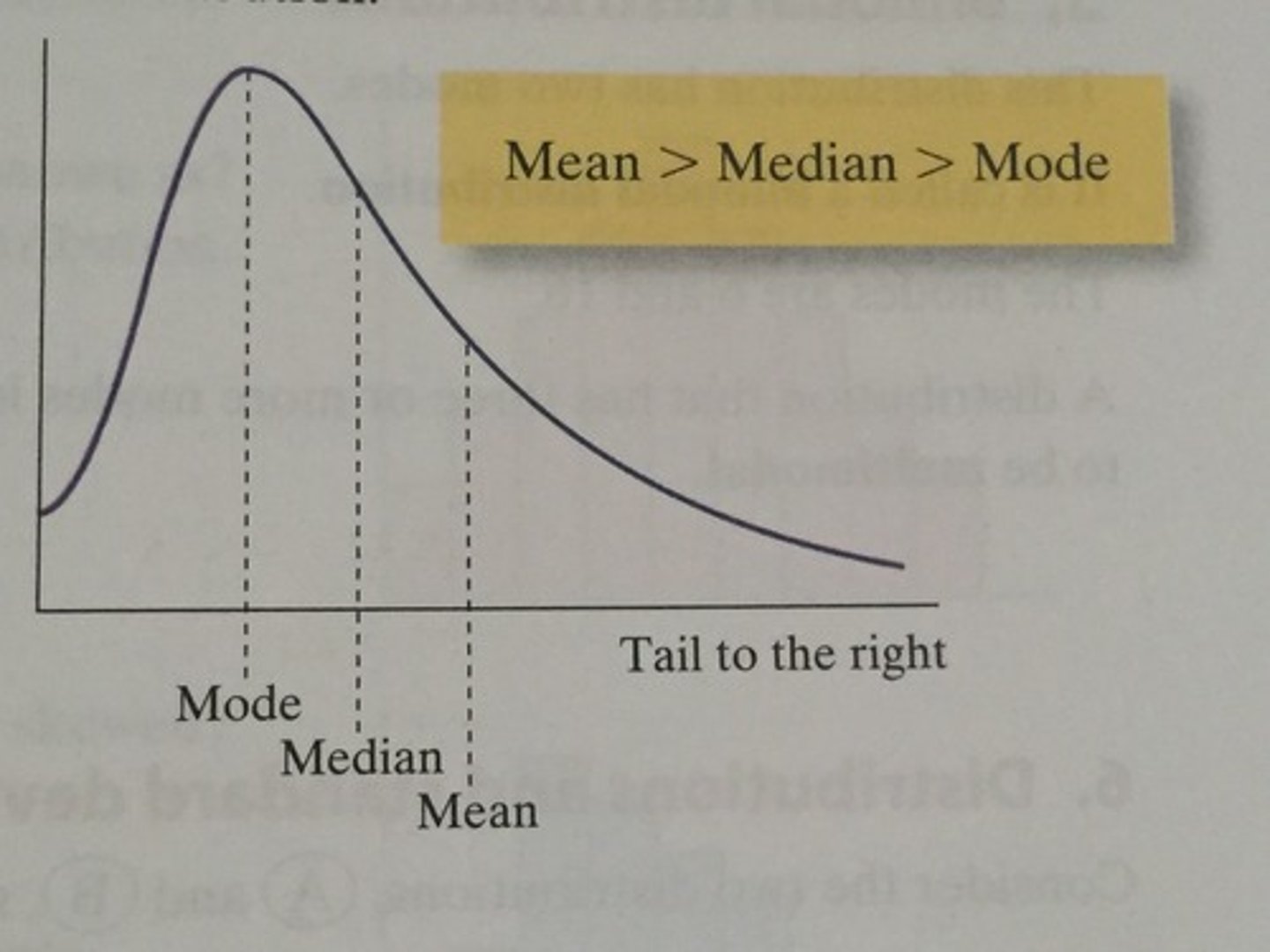
Mean more than Median

Median more than Mode

Just think MEAN

MEDIAN

MODE.

They are in alphabetical order (by size) when positive skew and the opposite when negative

Positive Skew graph

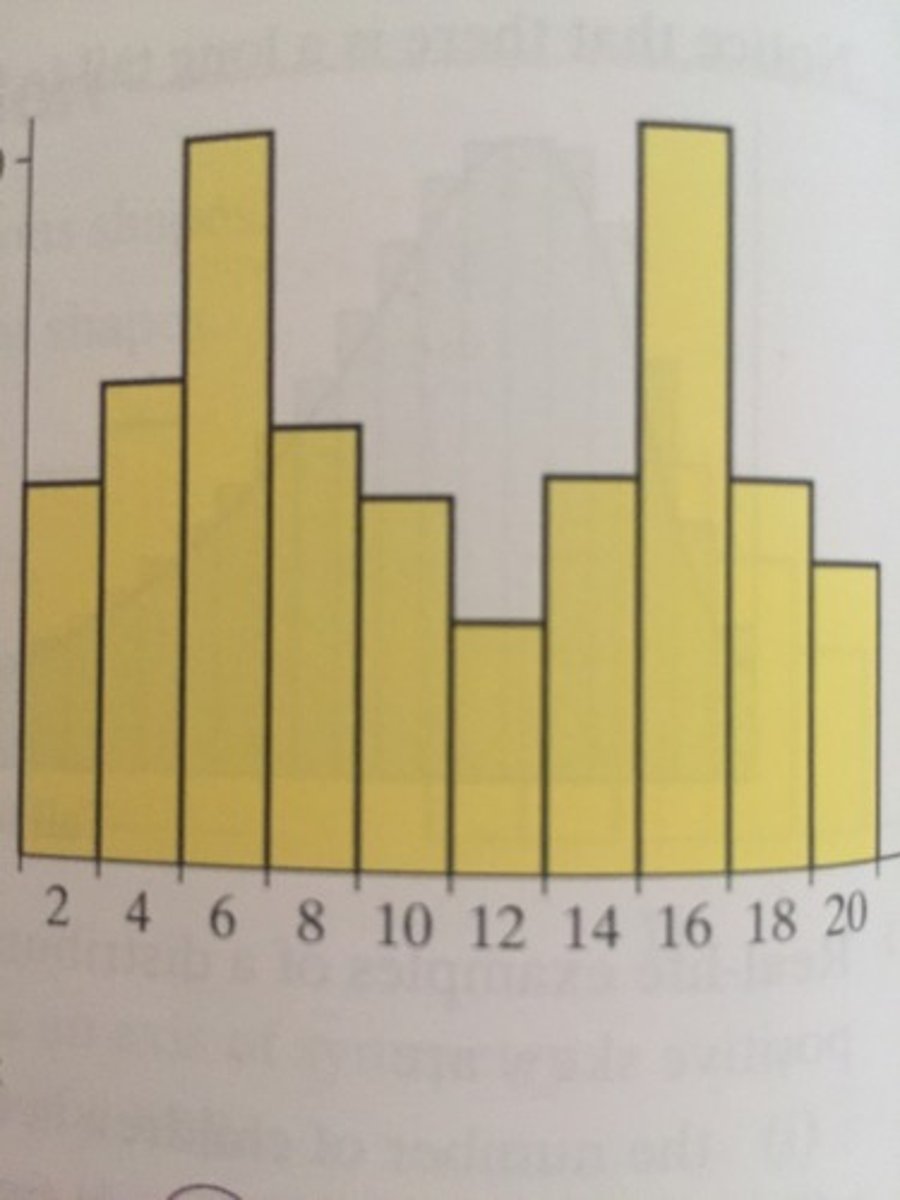
a distribution with two modes

bimodal distribution

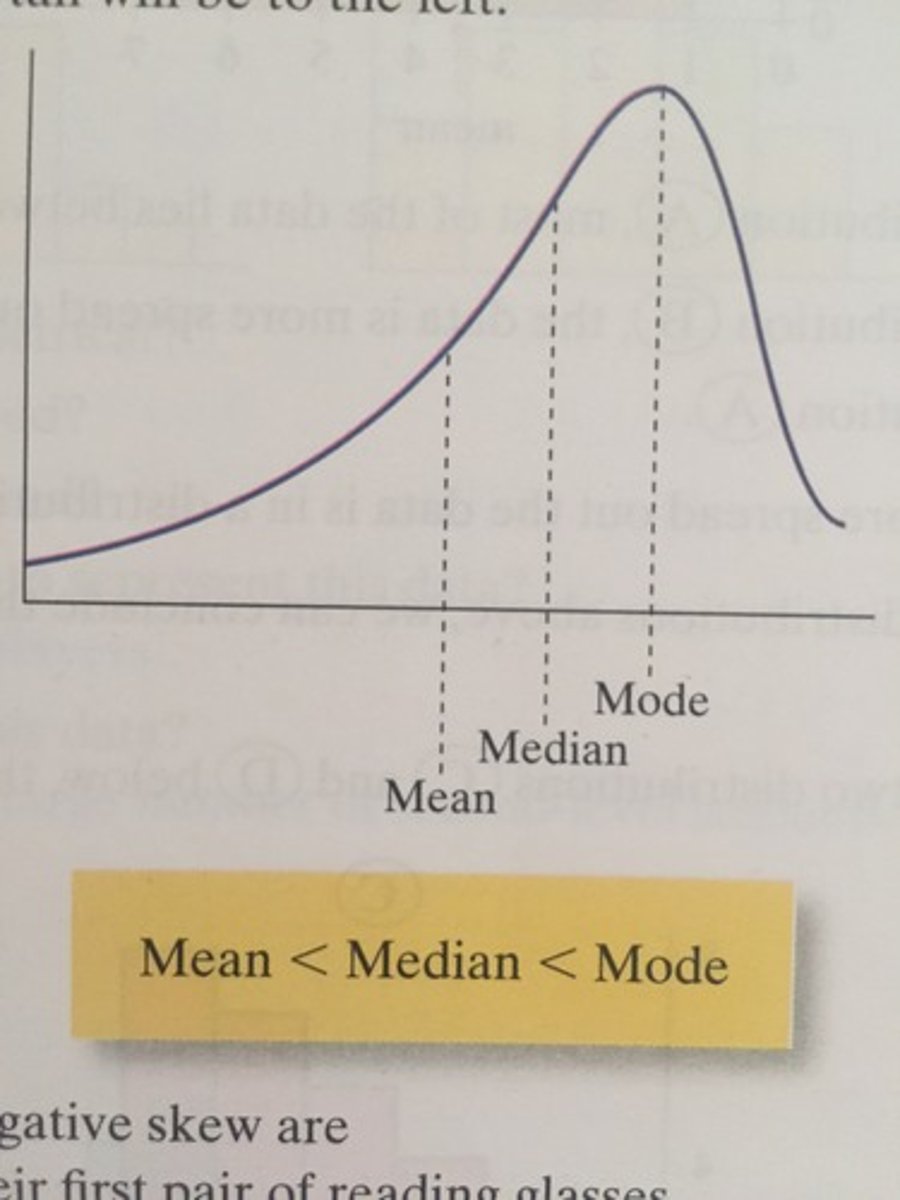
Mode more than Median

Median more than Mean

Negative Skew

the act of doing an experiment in probability

trial

the set or list of all possible outcomes in a trial

sample space

an outcome is one of the possible results of the trial

outcome

an event is the occurrence of one or more specific outcomes

event

(60/100)x 24= 14.4= 15th value (always round up with percentiles)

Given a list of 24 numbers, find the 60th percentile score.

less: (16/24)x100= 66.66%= 67% (always round up with percentiles)

If you got 64/100 (where this score is the 17th out of 24th highest score), calculate the percentile.

1 SD: 68%

2 SD: 95%

3 SD: 99.7%

The Empirical Rule

The mean of the sample means will be the same as the population mean.

The standard deviation will be the standard deviation of the population divided by root n (where n is number of participants)

Under the Central Limit Theorem how will will the mean and the standard deviation differ from the population?

1.96(standard deviation/ root n) in log tables

How to find a 95% confidence interval for the mean

We can use the standard deviation of the sample, if the sample has an n greater than 30.

Under the Central Limit Theorem, when we do not have a standard deviation for the population, what can we use?

In cases like a passcode that can have repeating digits, or days in a week etc. the digits, days etc. can be repeated. This means instead of 10×9×8… its (10)³ for all possibilities.

DON’T FORGET THIS COULD BE A SOLUTION TO PERMUTATIONS QUESTION.

Split into cases.

CASE 1: ALL DISTINCT DIGITS

9C3= 84

CASE 2: 2 SAME, 1 DIFFERENT

9X8= 72

CASE 3: ALL DIFFERENT

9

=165

How many unique 3-digit codes can be formed using the digits 1 to 9, if:

• Digits can be repeated in the code,

• The order of digits does not matter (e.g., 123, 231, and 312 are considered the same code)?

1. Calculate all possible ways and take away from number of ways it does NOT happen.

2. Split into individual cases.

2 IMPORTANT TRICKS

Explain why we use the choose function in Bernoulli trials.

12.11.10.9= 11880/4!= 495.

How can we choose a group of 4 actors from a team of 12, without using the combinations formula?

6!= 720 ways but since it is circle divide by 6= 120 ways

Explain how to arrange 6 people in a circular arrangements.

If we fix person 1 at the start of the circle and keep him there, then we can treat the remaining places as a regular permutation. (Think about it: perspective is all that matters in a circle and all the possible people will group around him when considering all outcomes)

What does “fixing” a person in a circular arrangement do?

profit/ cost price

Write formula for mark up

profit/ selling price

Write formula for margin

(amount of error/ true value).100

Write formula for percentage error

completing the square

x²- (sum of roots)x+ product of roots

equating coefficients

what should i look for in quadratic?

(a-b)(a²+ab+b²)

(a+b)(a²-ab+b²)

difference of two cubes formula

As x gets closer and closer to a certain value (eg 2, 3, infinity etc.), it will get closer and closer to a y-value. For example, (1/3)^x where x tends to infinity will equal 0 on the y-value. Equally, the y-axis is an asymptote.

What does a limit of a function measure?

An injective function has a unique output for every input.

A surjective function will have a codomain equal to its range.

A bijective function has both qualities.

Distinguish between injective, surjective and bijective functions.

Discontinuous (this is usually because the denominator equals 0)

How do you describe a function where a specific limit (eg at x=2) does not exist?

Firstly, what does 1m² measure in cm²?

100.100= 10,000cm² then multiplied by 7= 70,000cm²

Convert 7m² into cm²

1m³= 1m.1m.1m= 1000mm.1000mm.10000mm= 0.0007m³.

Convert 700,000 mm³ into m³

1cm³= 1cm.1cm.1cm

0.01m. 0.01m. 0.01m= 1/1,000,000m³.

0.1 divided by 1/1,000,000m³= 100,000cm³

Convert 0.1m³ into cm³.

When multiplying or dividing the expression by a negative number.

When do you change an inequality sign?

Its in the name the “lowest” common (as in same) “multiple”

2 multiples= 2,4,6, 8, 10, 12

3 multiplies= 3,6,9, 12

LCM is 6.

How to find the LCM of 2,3

factors of 12= 1,2,3, 4, 6, 12

factors of 16= 1,2,4,8, 16

What is the highest factor that is common to both?

4.

How to find HCF of 12, 16

14 multiplied by 2.

2 is a prime number

14 can be written as 7 multiplied by 2

so (2²x7)… all factors are prime.

Find the prime factors of 28

140= 70 and 2. 10 and 7. 5 and 2. so 7x5x(2)²

what are the prime factors of 140

3!= 6

It is 3! because this is a real-life sequence, not a probability table outlining all possibilites.

There are 3 delivery drivers and 3 packages. Each package must be delivered by exactly one driver, and no driver can deliver more than one package. In how many different ways can the packages be assigned to the drivers?

Package 1 has 3 possible drivers.

Package 2 has 3 possible drivers.

3.3=9

There are 3 delivery drivers: D1, D2, D3.
There are 2 packages: P1 and P2.

Each package must be delivered by any one of the 3 drivers, and drivers can deliver multiple packages (so reuse is allowed).

In how many different ways can the 2 packages be assigned to the drivers?

• When you have got a certain number of things “a”

• And you must assign them to a certain number of things “b”

• Powers will be used if repetition is allowed.

• Permutations will be used if repetition is not.

Key to spotting permutations/ power probability questions in unfamiliar scenario

(3)^5= 243 ways.

A multiple choice quiz has 5 questions with A, B and C as answers. How many ways can you answer this quiz?

Think logically:

“a” is our number of choices per “step”

“b” is our total number of steps.

EG Choose a 4-digit passcode from 10 digits where digits can be repeated.

(10)^4

10 is our total number of choices per step.

4 is the number of choices per step.

In (a)^b problems in probability, how do we determine the a and the b.

6C2. 4C2. 2C2= 90/ 3!= 15

You pick 2 from 6 for boat 1, 2 from 4 for boat 2 and boat 3 is then filled automatically.

However, in this combination you are counting AB and CD an EF as being different to CD, EF and AB. We want to find all the pairings, but we don’t really care about the order of the boats.

So we divide by 3! (the total ways of arranging the boats) as then we have the combination of pairs.

Let’s say you have a group of 6 people.

You must pair 2 people in 3 different boats.

How many different ways can you have pairs together in these boats?

(5)³= 125

Let’s say you have 3 art assignments to complete.

You can choose 5 themes for each art assignment (you can choose the same theme for all 3 in fact).

How many different ways can you assign these themes to your different projects?

There are 5 decisions to be made and 4 possible options so 4^5

Let’s say there are 5 customers arriving at a restaurant.
There are 4 tables available.
Each customer can choose any table to sit at.
(Multiple customers can sit at the same table — there’s no limit.)

How many ways can the customers sit at the table?

5³

A game show has 5 different prizes. There are 3 contestants, and each contestant can win any one of the prizes (prizes can be repeated).
How many different prize assignments are possible?

5.4.3.2= 120 (or 5P4)

So there are 120 potential permutations of 5 groups.

Then, 1 group can choose a strategy in (3)^4 ways

So 120. (3)^4 = 9720

So basically when we have the exact same permutation of the 120 groups. ie permutation 137 we consider them picking (from group 1 to group 5) Strategy 1, strategy 1, strategy 1, strategy 1, strategy 2 as different to picking strategy 1, strategy 1, strategy 1, strategy 2, strategy 1

A company has 5 different projects and 4 team members.

Each team member will be assigned to one different project (no two members work on the same project).

After assigning members, each project leader can choose one of 3 possible strategies for their project.

How many different ways are there to assign team members to projects and choose strategies?

The locus of point A refers to all the points which are x distance from point A

(think a circle and its radii)

What does the locus of point A refer to?

The 1.96

What should you not forget when calculating standard errors in statistics?

How to calculate the line of best fit in a scatter plot?

1+3=4/2=2

6+8= 14/2 =7

so 5

ALWAYS SPLIT DATA IN HALF AND FIND MEDIANS OF THESE “HALVES”.

IF YOU CANNOT DIVIDE EXACTLY IN HALF TAKE OUT THE ADDITIONAL MIDDLE NUMBER.

Find the interquartile range of 1,3,5, 6, 8

Think back:

consider that it could always be 1- specific probability and then all other conditions are met.

This is a trick you may need for maximising P(A), P(B), P(C)

Take an example eg hours exercised and points in match

Let’s say r= 0.9 This means that there is a very strong relationship between how much you exercise and your points..

The slope of the regression line will tell you how much your points increase for each additional hour you train.

Distinguish between slope of regression line and correlation coefficient

Imagine a hexagon, there will be 3

How many rectangles can you create from selecting 4 points in a hexagon?

3/23

A prize is hidden behind one of 10 identical doors. There is a 60% chance that the prize was hidden at all (i.e. someone actually put it there), and a 40% chance that no prize was placed behind any door.

If the prize was hidden, it is equally likely to be behind any of the 10 doors.

You open 9 doors, and find nothing behind them.
What is the probability that the prize is behind the 10th door?

4.25

You are allowed to roll a dice two times.

You play a game.

You can choose to stop after the first roll if you wish.

You will be paid x euros at the end of the game, where x is the value of your most recent dice throw.

How much are you expected to make from this game.

21.34%

Note in these problems its always just:

(Probability of event/ total probability)

eg here (probability of careless worker rating 4 as non-spam/ probability of any worker rating 4 as non-spam)

Amazon has a spam detection system in which 90% of raters are diligent, and 10% are careless. A diligent rater marks 80% of reviews as non-spam and 20% as spam. A careless rater, however, marks all reviews as non-spam. If a particular rater marks four consecutive reviews as non-spam, what is the probability that this rater is careless? Give your answer as a percentage, correct to 2 decimal places.

0.27 (approximately)

A machine produces items with the following defect probabilities:

• 10% are defective (D)

• 90% are non-defective (N)

Three items are selected at random.
What is the probability that at least one is defective and at least one is non-defective?

(a) 3/10

(b) 1/3

A bag contains 3 red balls and 2 green balls. Two balls are drawn without replacement.

Questions:

(a) What is the probability that both balls are red?
(b) Given that at least one red ball was drawn, what is the probability that both were red?

Create tree diagrams!

Always consider 1-p

Important “trick” in probability

Consider the tree diagram to help find the probability

That difficult a(n+1) question

Consider smaller intervals

Trick for finding slope of the line of best fit

1/2

When we pick 3 letters from the word BOOK, what is the probability that the selection contains 2 Os?

What is the probability that when picking 3 letters from MISSISSIPPI, you pick exactly 2 “I”?

You have 5 boys and 3 girls standing in a row, how many arrangements have no 2 girls seated together?

Let’s say we have a row of 5 boys and 4 girls. How many of these arrangements will have exactly 3 girls together?