Kins 304 Exam 2

linear distance

measured along the entire path of motion (scalar)

linear displacement

measured as the straight line between the initial and first position

-vector

linear speed

distance covered divided by time taken to cover

speed = l/change in time

linear pace

the taken to cover a specified distance

pace = time/distance

linear velocity

rate of change in location/position

linear acceleration

rate of change in linear velocity

-vector

a = V2-V1/change in time

SOHCAHTOA

SIN (Opposite/Hypotenuse) COS (Adjacent/Hypotenuse) TAN (Opposite/Adjacent)

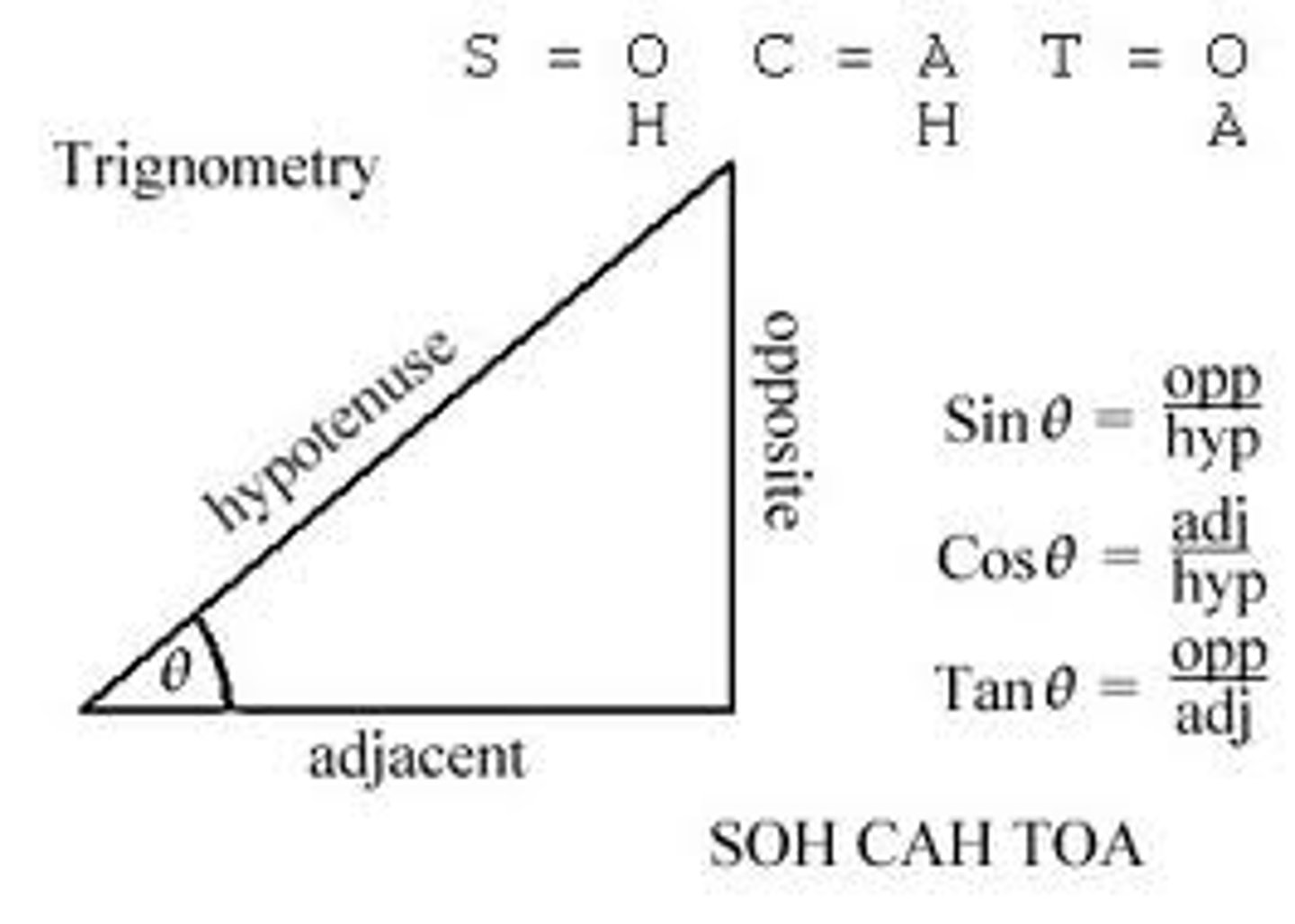
Pythagorean Theorem

a²+b²=c²

Law of Sines

sinA/a=sinB/b=sinC/c

Law of Cosines

a²=b²+c²-2bcCosA

b²=a²+c²-2acCosB

c²=a²+b²-2abCosC

vector composition

2+ vectors to create single vector

-tip to tail vector comp -> resultant vector

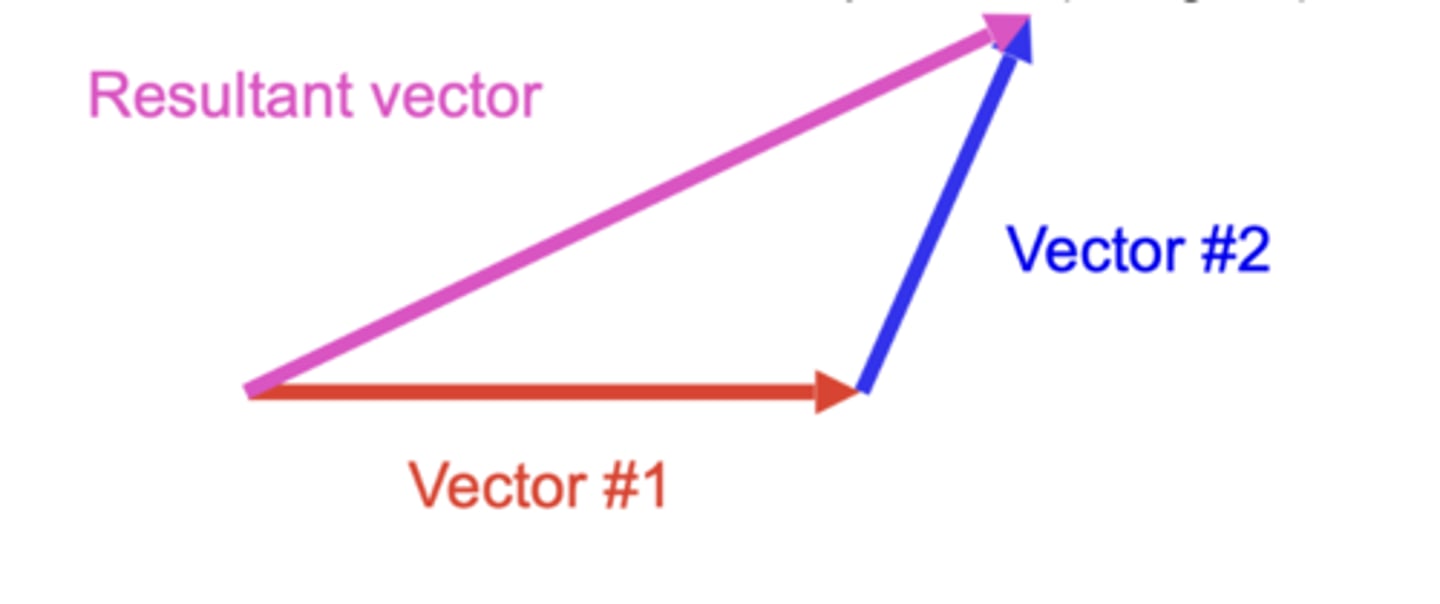
same direction vector

sum

opposite direction vector

difference

different orientation vectors

tip to tail

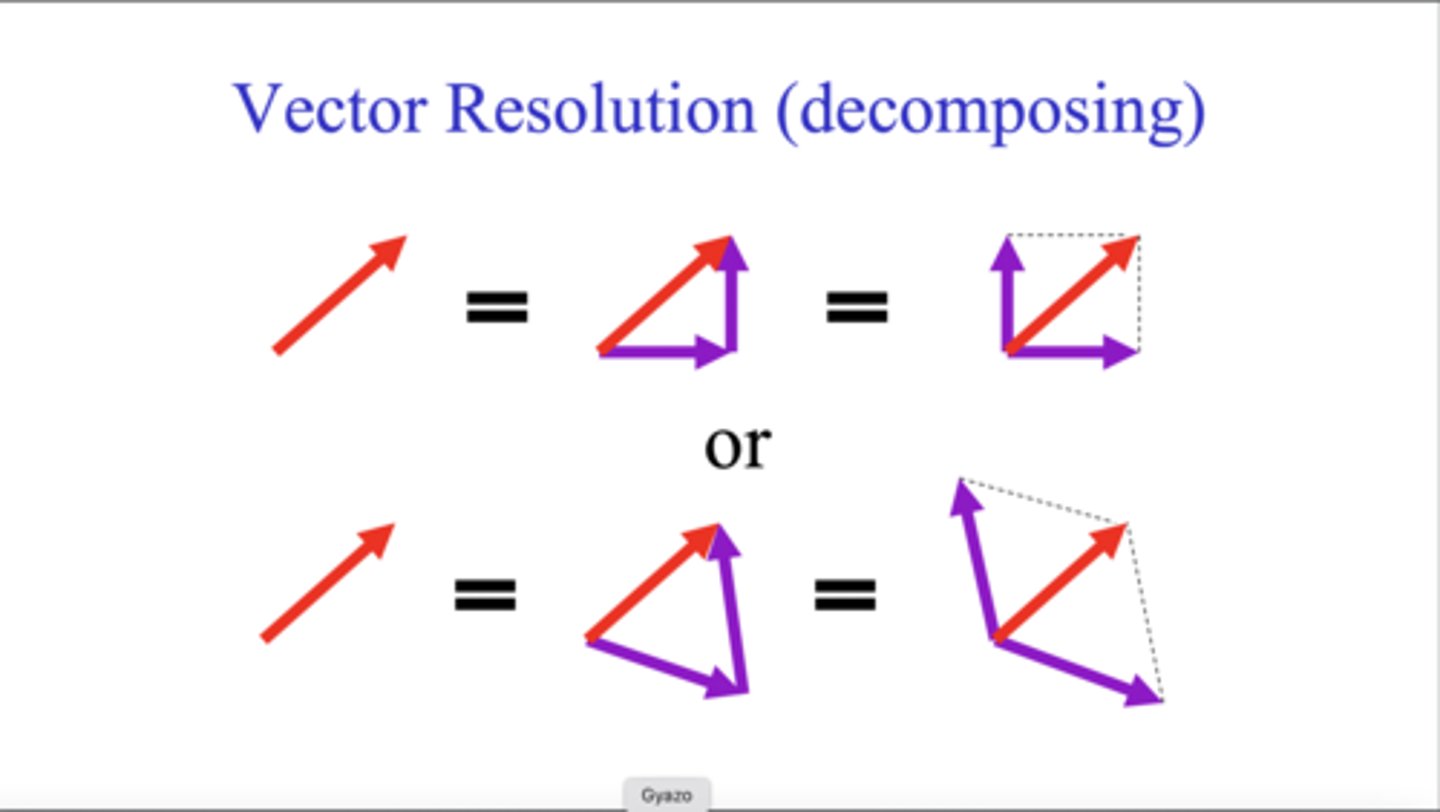
vector resolution

break down into horizontal and vector components

difference between average and instantaneous quantities?

average - occurring over designated time interval

instantaneous - occurring during small interval of time

what happens to vertical velocity of a ball being tossed up in the air?

velocity decreases prior to reach max height

projectile motion

bodies that move through the air unassisted

examples of projectile motion

baseball, shot put/ high/long jumper

vertical components of projectile

max height achieved

- influenced by gravity (-9.81m/s2)

horizontal components of projectile

distance the projectile travels

-no forces affect

vertical vs horizontal projectile example:

dropping a baseball vs bunting

Vertical = same

horizontal = different

3 factors that influence projectile trajectory

angle of projection, projection speed, relative projection height

change in projection angle

determines projectile trajectory

- vertical

-oblique

-horizontal

change in projection speed

magnitude of projection velocity

-affect range and height when other factors are constant

change in relative projection height

increase RPH -> increases flight time and horizontal displacement

your students are goofing around in gym class. they bet you that they can throw the ball hard enough to hit the ceiling. the students throw the ball velocity of 13m/s. if the ceiling is 10m tall, will the ball hit the ceiling?

V1 = 13/ms , ag = -9.81m/s2. height = 10m

0 = v1^2 + 2ad

0 = (13m/s)^2 + 2(-9.81m/s2)d

0 = 169m2/s2 + (-19.62m/s2)d

19.62m/s2(d)=169m2/s2 / 19.62m2/s2

= 8.61 m

you are trying to kick a soccer ball across the entire width of the field (50m). If the ball is kicked with a horizontal velocity of 14m/s with a flight time of 3.7s, how far was the kick?

Vh - 14m/s , t = 3.7s

d = Vh x t

d = 14m/s x 3.7 s

d = 51.8 m

a projectile is launched from the ground at an angle of 68 degrees with an initial velocity of 17m/s.

A) horizontal and vertical components?

B) how high does projectile go?

C) how far does projectile go

V1 = 17m/s ag= -9.81m/s2

A) horizontal: Cos = adj/hyp

cos 68 = vh/ 17m/s -> 0.375 = vh/ 17m/s -> vh = 6.37 m/s

veritcal: sin = opp/hyp

sin 68 = vv/17m/s -> 0.927 = vv/17m/s -> vv = 15.76 m/s

B) how high?

0 = v1^2 + 2ad

0 = (15.76m/s)^2 + 2(-9.81m/s2)d

0 = 248.38m2/s2 + (-19.62m/s2)d

19.62m/s2 (d) = 248.38m2/s2 / 19.62m/s2

= 12.66 m

C) how far?

0 = V1 + at

0 = 15.76m/s + (-9.81m/s2)t

9.81m/s2 = 15.76m/s / 9.81 -> t = 1.61 s

1.61s x 2 = 3.22s

dh = vh x t -> dh = 6.37m/s(3.22s)

dh = 20.51m

a swimmer orients himself perpendicular to the parallel banks of a river. If his velocity is 2m/s and the velocity of the current is 0.5m/s.

A) what is resultant velocity?

B)) how far will he actually have to swim to get to the other side of the bank if 50 m apart

a2+b2=c2

A) R2 = (2m/s)^2 + (0.5m/s)^2

R2 = 4.25

R = 2.06m/s

B) direction:

cos a = 2m/s / R

cos a = 2m/s / 2.06m/s -> 0.970

cos -1 (0.970) = 14 degrees

displacement:

cos a = 50m/D

cos 14 = 50m/D -> D(cos 14) = 50m -> D(0.970) = 50m / 0.970

D= 51.5m

soccer ball rolling down at t = 0, instantaneous velocity of 4m/s. If acceleration of ball is CONSTANT at 0.3m/s, how long will it take for a complete stop?

V1 = 4m/s V2 = 0 t1 = 0 a = -0.3m/s2

a = v2-v1/ change in time

-0.3m/s2 = 0-4m/s / t

-0.3m/s2 (t) = -4m/s / -0.3m/s2

t = 13.3 s

dennis decided to run 4 laps around a 400m track, ending in the same location as he began.

A) what is distance ran?

B) displacement?

C) dennis finished 4 laps in 7 minutes. what was his speed?

A) 4 x 400 m =1600m

B) displacement = 0

- not a straight line

C) speed:

7minutes = 60s/1min = 420s

speed = 1600m/420s

= 3.81m/s

angular distance

sum of all changes undergone by a rotating body

-total motion of path

angular displacement

change in angular position or orientation of a line segment

-difference of initial and final position

-vector, counter clockwise (+) vs clockwise (-)

angular speed

angular distance divided by the time that the motion occued

-scalar

- angular speed = angular distance change in time

angular velocity

angular displacement covered in time given

- vectori, direction +/- or counterclockwise vs clockwise

angular acceleration

rate of change in angular velocity

a = w2-w1/t2-t1

positive angular acceleration

increase angular velocity in positive direction

OR

decrease angular velocity in negative direction

negative angular acceleration

decrease angular velocity in positive direction

OR

increase angular velocity in negative direction

linear positive acceleration

increase velocity in positive direction

or

decrease velocity in negative direction

linear negative acceleration

decrease velocity in positive direction

or

increase velocity in negative direction

apex

highhest point in trajectory of projectile

trajectory

flight path of a projectile

range

horizontal displacement of projectile landung

flight time influenced

initial vertical velocity and relative projection height

horizontal displacement influenced

horizontal velocity and relative projection height

vertical displacement influenced

initial vertical velocity and relative projection height

trajectory influenced

angle of projection, projection speed, and relative projection height

OPH

optimal projection angles

RPH = 0

best angle = 45 defrees

linear vs angular distance

linear - measured along a path

angular - sum of all changes in a rotating body

linear vs angular displacement

linear - straight line (first->second)

angular - change in angular position (different from initial and final)

-counterclockwise/clockwise

linear vs angular spped

linear - distance covered

angular - angular distance/time

linear vs angular velocity

linear - rate of change in location

angular - displacement covered in time

- clockwise/counterclockwise

Linear vs Angular Acceleration

linear: change in velocity in straight line

angular: change in rate of rotation

difference in joint angles and body segment orientation

joint angle - angle between anatomical position (0 degrees)

-relative angle

body segment- angular orientation of a body segment with a fixed line reference

-absolute angle

relationship between linear and angular distance

during angular motion, greater the radius between a given point on a rotating body and axis of rotation, greater linear distance undergone by point of interest

relationship between linear and angular velocity

all other factors held constant, the greater radius of a rotating body = greater linear velocity

tangential acceleration

represents the change in linear speed for a body traveling on a curved path

at = v2-v1/t

at = tangential acceleration

v1 = initial linear velocity

v2 = second linear velocity

t = time interval velocities assessed

Radial accerleration

represents change in direction of a body in angular motion

ar = v2/r

ar = radial acceleration

v = linear velocity of moving body

r = radius rotation

tangential and angular acceleration relationship

at = ar

at - linear acceleration (tang accel)

a = angular acceleration

r = radius of rotation

during a bicep curl, the elbow joint flexes 120 degrees. If you performed 15 reps, what is the total angular distance completed?

120 degrees x 2 = 240 degrees

240 degrees x 15 reps = 3600 degrees

you do 5 bicep curls at 90 degrees (anatomical position)

A)distance?

B)isplacement?

C)form change?

A) 90 x 10 = 900

5 bicep curls = up , + 5 more for down

B) displacement = 0 degrees

C) when form changes, angles, displacement and distance all change

a golf ball is struck with an angular velocity of 20rad/s. If the length of the club is 1.1m...

what is the linear velocity at the point of contact?

r1 = 1.1m

w1=20rad/s

v=rw

v= (1.1m)(20rad/s)

= 22 m/s

two baseballs are consecutively hit by a bat. The first ball is hit 0.2m from the bats axis of rotation and the SECOND ball is hit 0.4m from the bats axis of rotation. If the angular velocity of the bat is 30 rad/s at the instant both balls were contracted....

what was the linear velocity of bat at the two contact points?

A) r1 = 0.2m w1=30rad/s

v=rw

v =(0.2m)(30rad/s)

= 6m/s

B) r2 = 0.4m w2= 30 rad/s

v=rw

v=(0.4m)(30rad/s)

=12m/s

a windmill-style softball pitcher executes a pitch of 0.65s. If her pitching arm is 0.7m long....

A) what are the magnitudes of the TANGENTIAL and RADIAL acceleration on the ball just before ball release when the ball velocity is 20m/s

B) what is the magnitude of the total acceleration on the ball at the point of release?

t = 0.65s r = 0.7m v2 = 20m/s

A) at = v2-v1/change in t

at= 20m/s - 0m/s / 0.65s

at=30.8m/s2

ar= v2/r

ar=(20m/s)2 / 0.7m

ar= 571.4m/s2

B) a2 = at2 + ar2

a2 = (571.4m/s2)2 + (30.8m/s2)2

a=572.2m/s2

a discus thrower executes the throw in 2.5 seconds. If the throwing arm is 0.83m long..

A) what are the magnitudes of the TANGENTIAL and RADIAL acceleration of the disc just before the release when the tangential velocity is 22m/s

B) what is the magnitude of the total accerleration?

t = 2.5 s r = 0.83m v2 = 22m/s

A)

at=v2-v1/change in t

at = 22m/s- 0m/s / 2.5s

at = 8.8m/s2

ar=v2/r

ar=(22m/s)^2 / 0.83

ar= 583.13m/s2

B) a2= at2 + ar2

a2 = (8.8m/s2)2 + (583.13m/s2)2

a2 =340118.0369m2/s4

a=583.20m/s2

swimmer crosses lake 0.9km wide for 30minutes.

a) velocity?

b) average speed?

a) v = d/t

t= 30min d=0.9km

30 min = .5 hour

v = 0.9 km / 0.5 hr

= 1.8 km/hr

b) cant do speed, no distance

the score was tied 20-20 between Vikings and Packers. At the end of the game, the Vikings had an opportunity to kick the winning field goal. The ball was placed 42m from goalpost. If the ball was kicked horizontal component of initial velocity of 19m/s and flight time of 2.4s...

was the kick long enough to make field goal?

vh = 19m/s t = 2.4 s d = 42m

d=vh x t

d = 19m/s x 2.4s

= 45.6 m

yes it was long enough!

a volleyball is deflected vertically by a player during a block. The high school gym has a ceiling clearance of 10.5m. If the initial velocity of the ball is 14m/s...

will the ball hit the ceiling?

v1 = 14m/s ag= -9.81m/s2 height = 10.5m

0 = v12 + 2ad

0 = (14m/s)2 + 2(-9.81m/s2) x d

19.62 m/s2 x d = 196m2/s2

d=9.99 m

will not hit the ceiling

a soccer ball is kicked at a 40 degree angle with an initial velocity of 10m/s

a) how high does the ball go?

b) how far does the ball go?

v1 = 15m/s ag = -9.81m/s

horizontal:

cos 40 = vh/10m/s

10m/s x 0.766 = vh

vh = 7.66m/s

vertical:

sin 40 = vv/10m/s

10m/s x 0.643 = vv

vv = 6.43m/s

a) 0 = v12 + 2ad

0 = (6.43m/s)2 + 2(-9.81m/s2) x d

19.62m/s x d = 41.34m2/s2

d= 2.11 m high

b) 0 = v1 + at

0 = 6.43m/s + -9.81m/s2 x t

9.81m/s2 x t = 6.43m/s

t = 0.655 x 2

t = 1.31

dh=vht

dh= 7.66m/s x 1.31 s

= 10.03m far