Chapter 28: Special Relativity

classical velocity addition

the method of adding velocities when 𝑣<<𝑐; velocities add like regular numbers in one-dimensional motion: 𝑢=𝑣+𝑢′, where 𝑣 is the velocity between two observers, 𝑢 is the velocity of an object relative to one observer, and 𝑢′ is the velocity relative to the other observer

first postulate of special relativity

the idea that the laws of physics are the same and can be stated in their simplest form in all inertial frames of reference

inertial frame of reference

a reference frame in which a body at rest remains at rest and a body in motion moves at a constant speed in a straight line unless acted on by an outside force

length contraction

𝐿, the shortening of the measured length of an object moving relative to the observer’s frame: L=L0⁢√1−𝑣2𝑐2=𝐿0𝛾

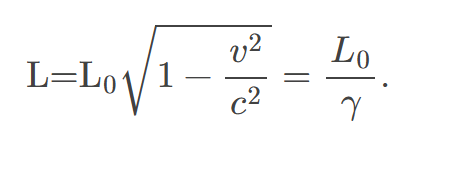
Michelson-Morley experiment

an investigation performed in 1887 that proved that the speed of light in a vacuum is the same in all frames of reference from which it is viewed

proper length

𝐿0; the distance between two points measured by an observer who is at rest relative to both of the points; Earth-bound observers measure proper length when measuring the distance between two points that are stationary relative to the Earth

proper time

Δ⁢𝑡0. the time measured by an observer at rest relative to the event being observed: Δ⁢𝑡=Δ⁢𝑡0√1−𝑣2𝑐2=𝛾⁢Δ⁢𝑡0, where 𝛾=1√1−𝑣2𝑐2

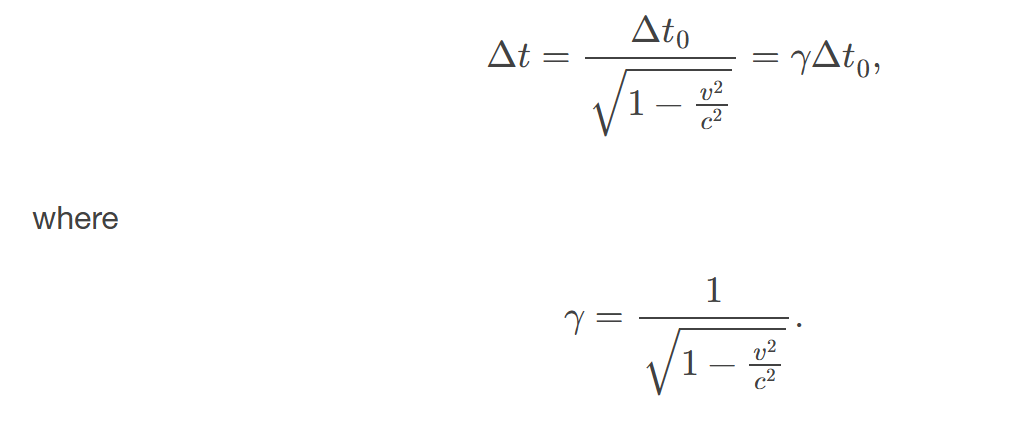
relativistic Doppler effects

a change in wavelength of radiation that is moving relative to the observer; the wavelength of the radiation is longer (called a red shift) than that emitted by the source when the source moves away from the observer and shorter (called a blue shift) when the source moves toward the observer; the shifted wavelength is described by the equation 𝜆obs⁢=λ𝑠⁢√1+𝑢𝑐1−𝑢𝑐 where 𝜆obs is the observed wavelength, 𝜆𝑠 is the source wavelength, and 𝑢 is the velocity of the source to the observer

relativistic kinetic energy

the kinetic energy of an object moving at relativistic speeds: KErel=(𝛾−1)⁢𝑚𝑐2, where 𝛾=1√1−𝑣2𝑐2

relativistic momentum

𝑝, the momentum of an object moving at relativistic velocity; 𝑝=γmu, where 𝑚 is the rest mass of the object, 𝑢 is its velocity relative to an observer, and the relativistic factor 𝛾=1√1−𝑢2𝑐2

relativistic velocity addition

the method of adding velocities of an object moving at a relativistic speed: u=𝑣+𝑢′1+𝑣⁢𝑢′𝑐2, where 𝑣 is the relative velocity between two observers, 𝑢 is the velocity of an object relative to one observer, and 𝑢′ is the velocity relative to the other observer

relativity

the study of how different observers measure the same event

rest energy

the energy stored in an object at rest: 𝐸0=𝑚𝑐2

rest mass

the mass of an object as measured by a person at rest relative to the object

second postulate of special relativity

the idea that the speed of light 𝑐 is a constant, independent of the source

special relativity

the theory that, in an inertial frame of reference, the motion of an object is relative to the frame from which it is viewed or measured

time dilation

the phenomenon of time passing slower to an observer who is moving relative to another observer

total energy

defined as 𝐸=𝛾𝑚𝑐2, where 𝛾=1√1−𝑣2𝑐2

twin paradox

this asks why a twin traveling at a relativistic speed away and then back towards the Earth ages less than the Earth-bound twin. The premise to the paradox is faulty because the traveling twin is accelerating, and special relativity does not apply to accelerating frames of reference

relativistic work-energy theorem

states that the work done on an object is equal to the change in its relativistic energy, taking into account both kinetic and potential energy in relativistic contexts.

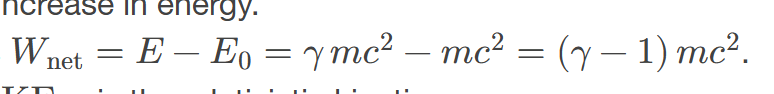
Relativistic kinetic energy

Refers to the energy an object possesses due to its motion at relativistic speeds, calculated as (E_k = \gamma mc^2 - mc^2), where (\gamma) is the Lorentz factor.

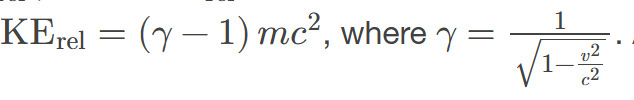
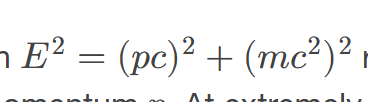
The equation 𝐸2=(⁢𝑝𝑐⁢)2+(⁢𝑚𝑐2)2 relates

relates the relativistic total energy 𝐸 and the relativistic momentum 𝑝. At extremely high velocities, the rest energy 𝑚𝑐2 becomes negligible, and 𝐸=𝑝𝑐.