MAT flashcards

a+ar+ar²+…+ar^(n-1)

Geometric series, a(1-r^n)/1-r if r ≠1

a+ar+ar²+ar³+…

sum to infinity of a geometric sequence, equals a/1-r if |r|<1. diverges otherwise

a+(a+d)+(a+2d)+…+(a+(n-1)d)

arithmetic series sum n/2(2a+(n-1)d)

cos²(x)

1-sin²x

sin²(x)

1-cos²x

pythagoras a²+b²=c²

sin(90-x)

cosx

cos(90-x)

sinx

sin(-x)

-sinx

cos(-x)

cosx

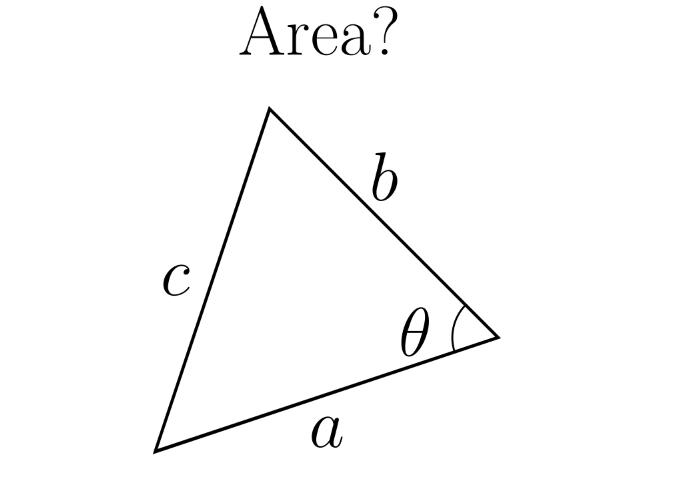
1/2absinx

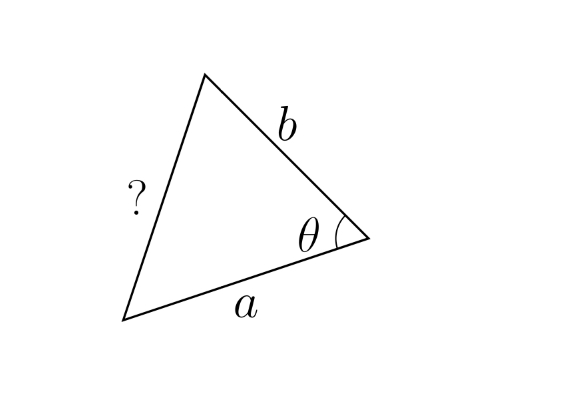
cosine rule c²=a²+b²-2abcosx

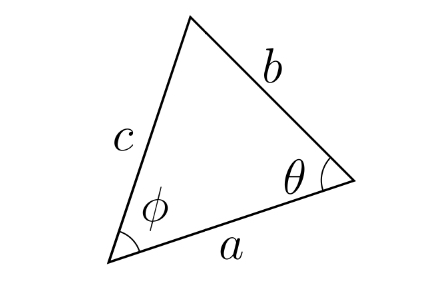
sine rule sinx/c = siny/b

y=m(x-x1)+y1

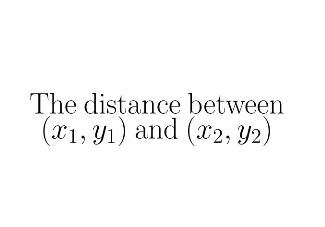
sqrt (x2-x1)² + (y2-y1)²

(x-a)²+(y-b)²=r²

circle with centre (a,b) and radius r

the lines y=m1x+c1 and y=m2x+c2 are perpendicular

m1m2=-1

the lines y=m1x+c1 and y=m2x+c2 are parallel

same gradient m1=m2

f(x+a)

translate by a units in the negative direction parallel to x axis

f(ax)

stretch by factor of 1/a parallel to the x axis

f(ax+b)

translation by b units in the negative direction parallel to x axis then stretch by factor of 1/a parallel to the x axis

(a^m)^n

a^(mn)

(a^m)(a^n)

a^(m+n)

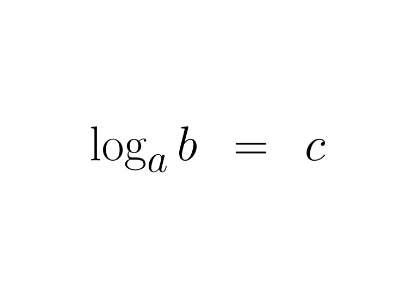
b=a^c

y=x^a

dy/dx=?

ax^(a-1)

y=e^(kx)

dy/dx=?

ke^(kx)

tangent to y=f(x) at x=a

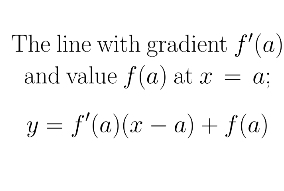
normal to y=f(x) at x=a

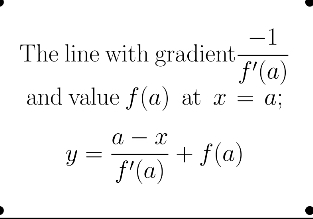
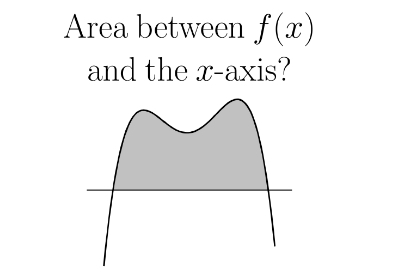
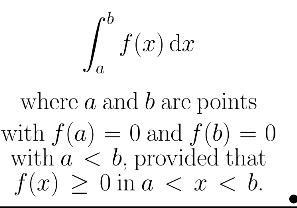
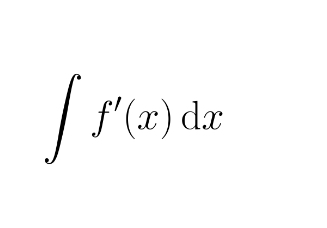
f(x) + c for some constant c

(x+y)^n

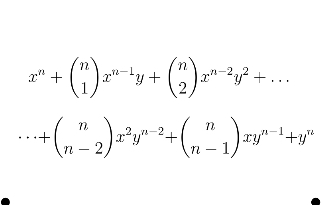
the number of ways to choose r from n things, order doesnt matter

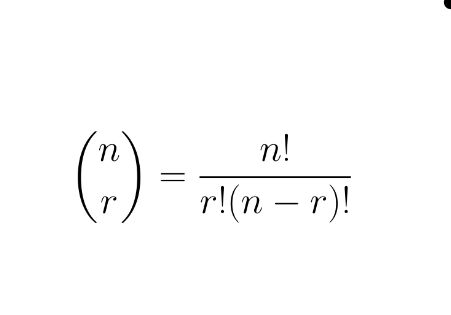
the number of ways to choose r things from n things, order matters

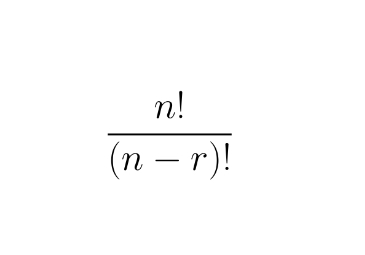
given n independent events, each with probability p of success, whats the probability of exactly r successes?

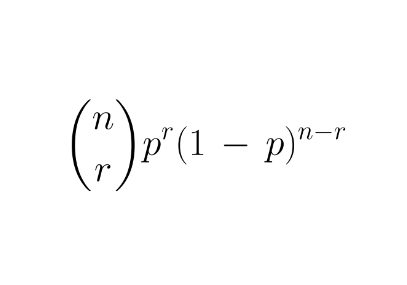
when does ax² + bx + c = 0 have exactly two real solutions”?

IFF b²-4ac>0

polynomial p(x) has a root at x=a

factor theorem, so p(x)=(x-a)q(x) for some polynomial q(x)

polynomial p(x) has a repeated root at x=a

therefore p(x) = (x-a)²q(x) for some polynomial q(x)

prime number, p

the only factors of p are 1 and p

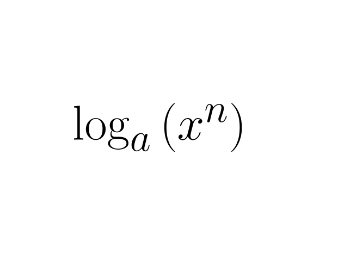
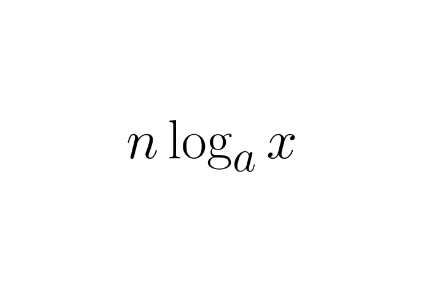
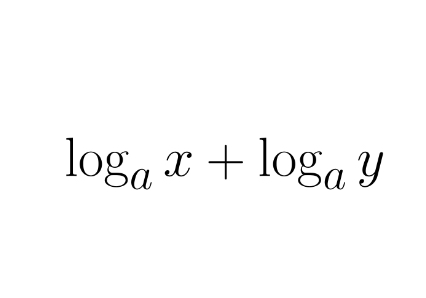
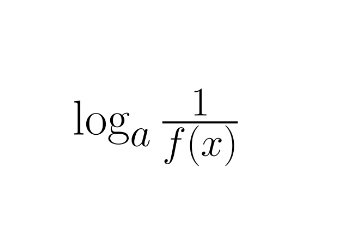
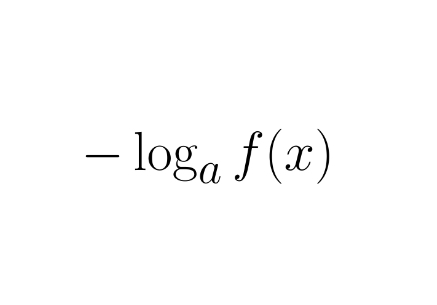
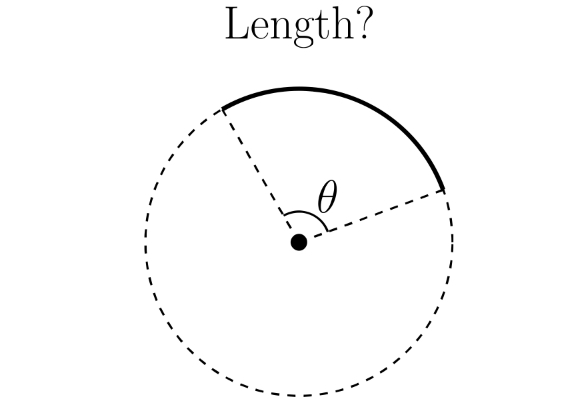
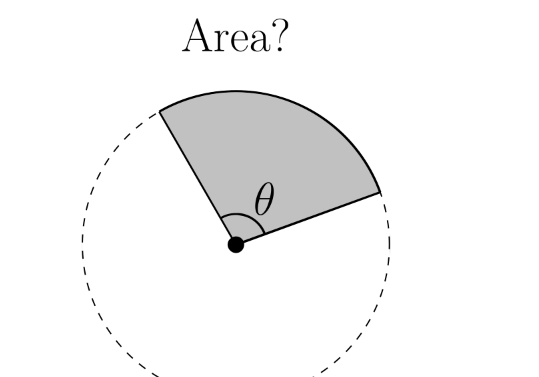
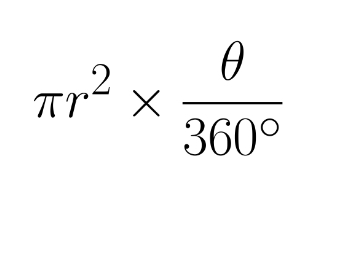
another way to write ax² + bx + c

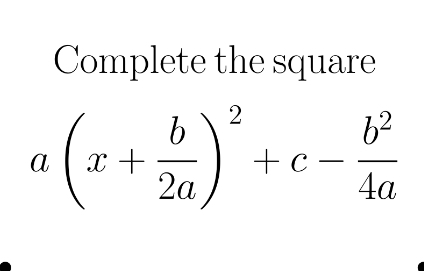
a² - b²

difference of two squares (a-b)(a+b)

(f(x))²

(f(x))² >= 0 for all x

turning point of f(x)

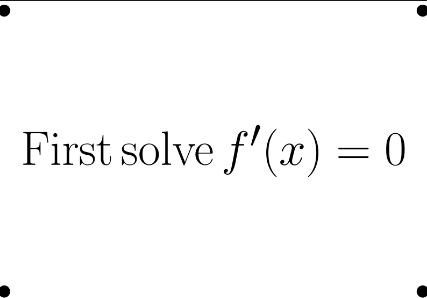
maximum of a function

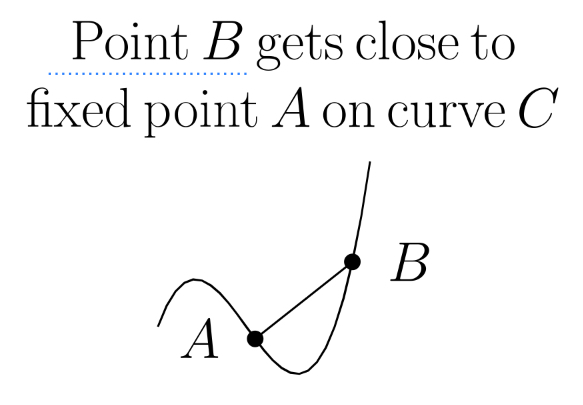
the gradient of the line AB gets close to the gradient of C at A

solve f(x)=g(x)

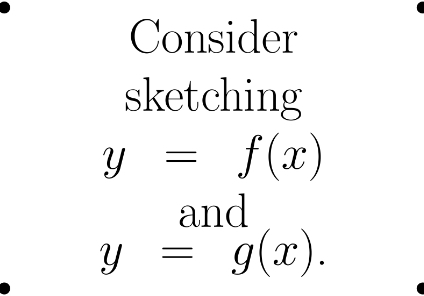
cos(x+360)

cosx

sin(x+360)

sinx

tan(x+180)

tanx

cos(180-x)

-cosx

sin(180-x)

sinx

tan(90-x)

cotx

displacement vector from (x1,y1) to (x2, y2)

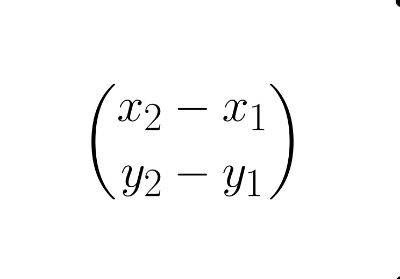
non-zero vectors a and b are parallel

a = kb for some real number k