Gravitational Fields

ADD GRAV FIELDS IS1 NOTES

Examples of natural satellites:

Moon, Earth, Sun

How do natural satellites stay in orbit?

• As the satellite is launched into space, it will constantly be attracted to the Earth

• If the Earth and satellite fall at the same rate, the satellite will orbit

Equation for orbital speed:

v = sqrt(GM/r)

Low Earth orbit satellites

• Satellites with a low distance from the Earth

• r is low, implying that orbital speed is high

Uses of low Earth orbit satellites:

Observation and remote sensing

Geostationary satellites

• Far away from the Earth

• Appear to be stationary on Earth (in one fixed position)

• Must be above the equator, rotate in the same direction and have a time period of 24 hours

Uses for geostationary satellites:

Communications, weather, television

Gravitational Potential

The work done per unit mass to move an object from infinity to that point

Gravitational Potential equation

V_g = -Gm/r as r → ∞, Vg → 0

Gravitational Potential energy

The work done to move a mass from infinity to a point in a gravitational field

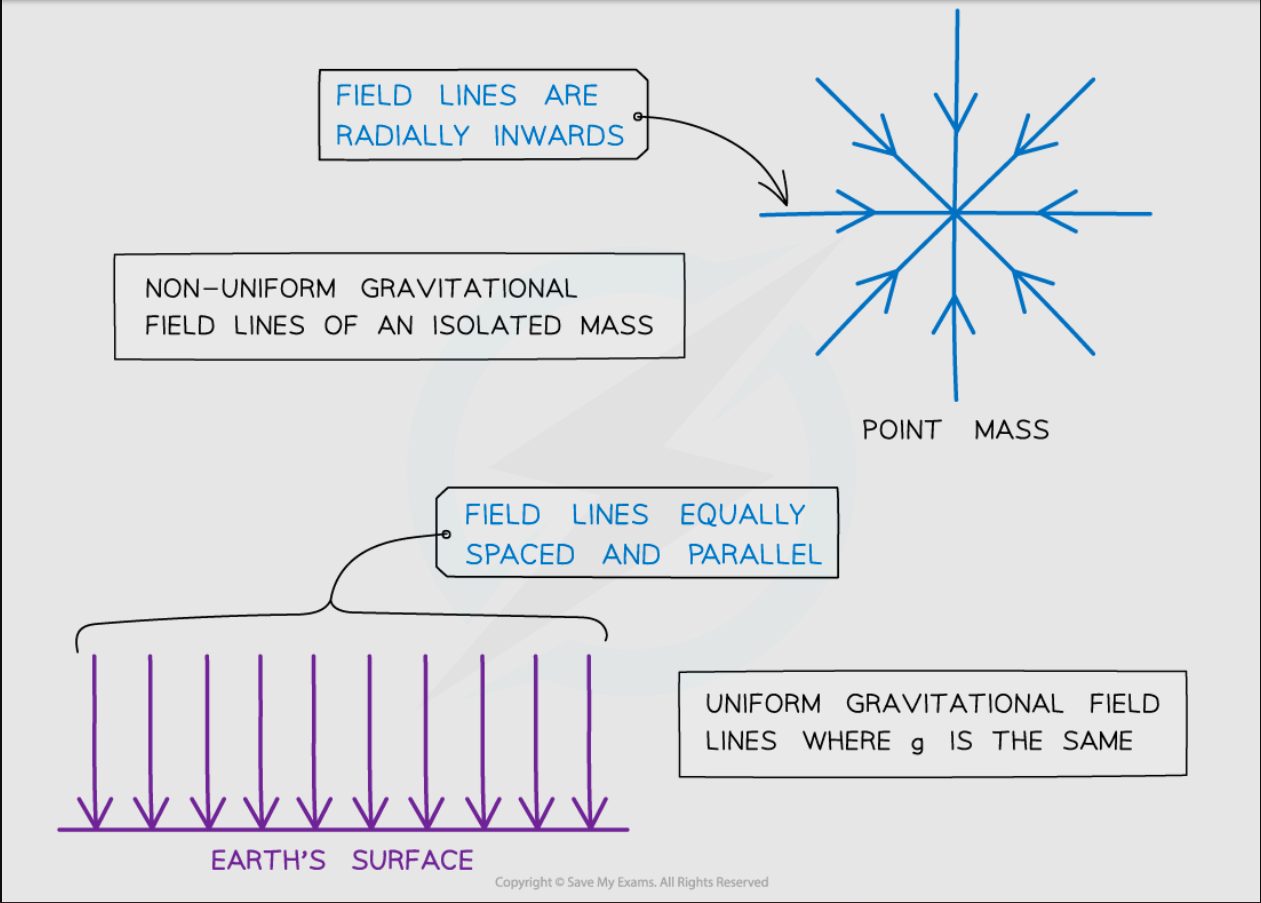
Uniform grav. field vs radial grav. field

A uniform grav. field is an approximation for where field lines are parallel, but radial grav. field lines point towards a central mass

Change in Gravitational Potential energy equation

• ΔE = mΔV_g

• In radial fields, E = -GMm/r

The area of a force-radius graph

The change in G.P.e

Escape velocity

The minimum speed an object needs to escape the gravitational field of a body

Escape velocity equation and derivation

• E_k = E_p

• ½mv² = GMm/r

• v = sqrt(2GM/r), where r is the distance from the surface of the body

Kepler’s Third Law derivation

• Assume a circular planetary orbit

• Centripetal force to keep the planet in orbit is provided by the Gravitational Force between the Sun and Planet

• F = mv²/r = GMm/r²

• r³=(GM/4π²)T²

• Therefore, r³ ∝ T²

K3’s Law for linear velocity:

• v² = GM/r

• v = 2πr/T

How does gravitational potential vary between the Earth and Moon?

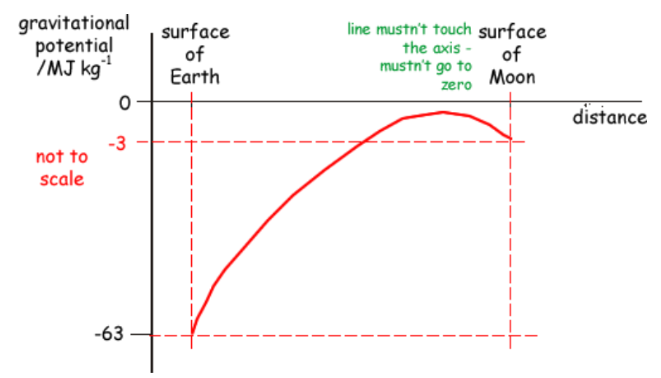
Change in gravitational potential formula + derrivation

• Distance from r₁ to r₂

• V_g1 = -GM/r₁

• V_g2 = -GM/r₂

• ΔV_g = V_g2 - V_g1

• = -GM/r1 + GM/r2

Total energy equation

Total energy = E_k + E_p

A satellite with mass 200kg has a velocity of 5.6 × 10³ ms^-1 and has a circular orbit of 1.28 × 10^7m around the Earth. Given the mass of the Earth is 6 × 10^24 kg, what is the potential energy of the satelite?

• E_k = 1/2mv² = 3.14 × 10^9J

• E_p = -GMm/r = -6.25 × 10^9J

• T = E_k + E_p = -3.11 × 10^9J

Escape velocity is independent of:

Escape velocity is independent of mass

Gravitational field

A field created around any object with mass, extending to infinity but diminishing as distance from the centre of mass increases

Gravitational field strength

The gravitational force exerted per unit mass to a point within a gravitational field

Gravitational field lines

Lines of forced used to map gravitational field patterns around an object with mass

Radial field

A symmetrical field that diminishes with distance from its centre, eg a gravitational field around a sphere

Point mass

A mass with negligible volume

Uniform gravitational field

A gravitational field where the field lines are equidistant, parallel and the value of the gravitational field strength is constant

Newton’s law of gravitation

• The force between two masses is directly proportional to the product of the masses

• The force between two masses is direction proportional to the square of the separation between them

• F = -GMm/r²