Abeka Plane Geometry Test 2

false

the whole is greater than the sum of all its parts

true

all right angles are equal

false

two angles that are complementary to the same angle or equal angles are supplementary to each other

true

a quantity may be substituted for its equal in any process

false

two straight lines can intersect in several points at one time

false

if the sum of two adjacent angles is a straight angle then they are complementary angles

false

the sum of two sides of a triangle is less than the third side

false

the sum of all the angles about a given point is a traight angle

true

two right triangles are congruent if the two legs of one triangle are equal respectively to the two legs of the other triangle

false

CPCTE can be used as a reason for why two triangles are congruent

false

the eye is a calid means for testing the truth of a construction

true

a diameter of a circle is also a chord

corollary

a geometric statement that is easily deduced from a theorem

analysis

a pre proof planning of how a complete a proof

theorem

a geometric statement that is not self evident but proven by a chain of reasoning

construction

a figure that satisfies given conditions and is drawn without instruments of measurement

postulate

a geometric statement that is accepted without proof to be true

diameter

a radius of a circle is equal to half the length of the

auxiliary

added lines in a diagram used to aid in solving proofs are called

quadrant

the arc that represents one quarter of a circle is a

a straight angle

the sum of all the angles about a point on one side of a straight line

proof or demonstration

the process of reasoning that establishes the truth of a theorem or the correctness of a construction is called a

point

a line can be bisected by but one

congruent

two geometric figures that have the same shape and size are

a straight line

the shortest line that can be drawn between two points is

vertical of opposite

any two straight lines intersect to form equal

compass

the instrument used for drawing circles is the

corresponding

in two congruent figures the equal parts are called

AB=JK BC=KL CA=LJ

If Tri ABC is congruent to Tri JKL list the three pairs of equal angles

Angle CAB = Angle FEG

Angle ABC = Angle EGF

Angle BCA = Angle GFE

If Tri CAB = Tri FEG list the three pairs of equal angles

If equals are added to equals the sums are equal

Given: AB=DE BC=EF

Prove: AC=DF

if equals are subtracted from equals the remainders are equal

Given: AB=AC DB=EC

Proven: AD= AE

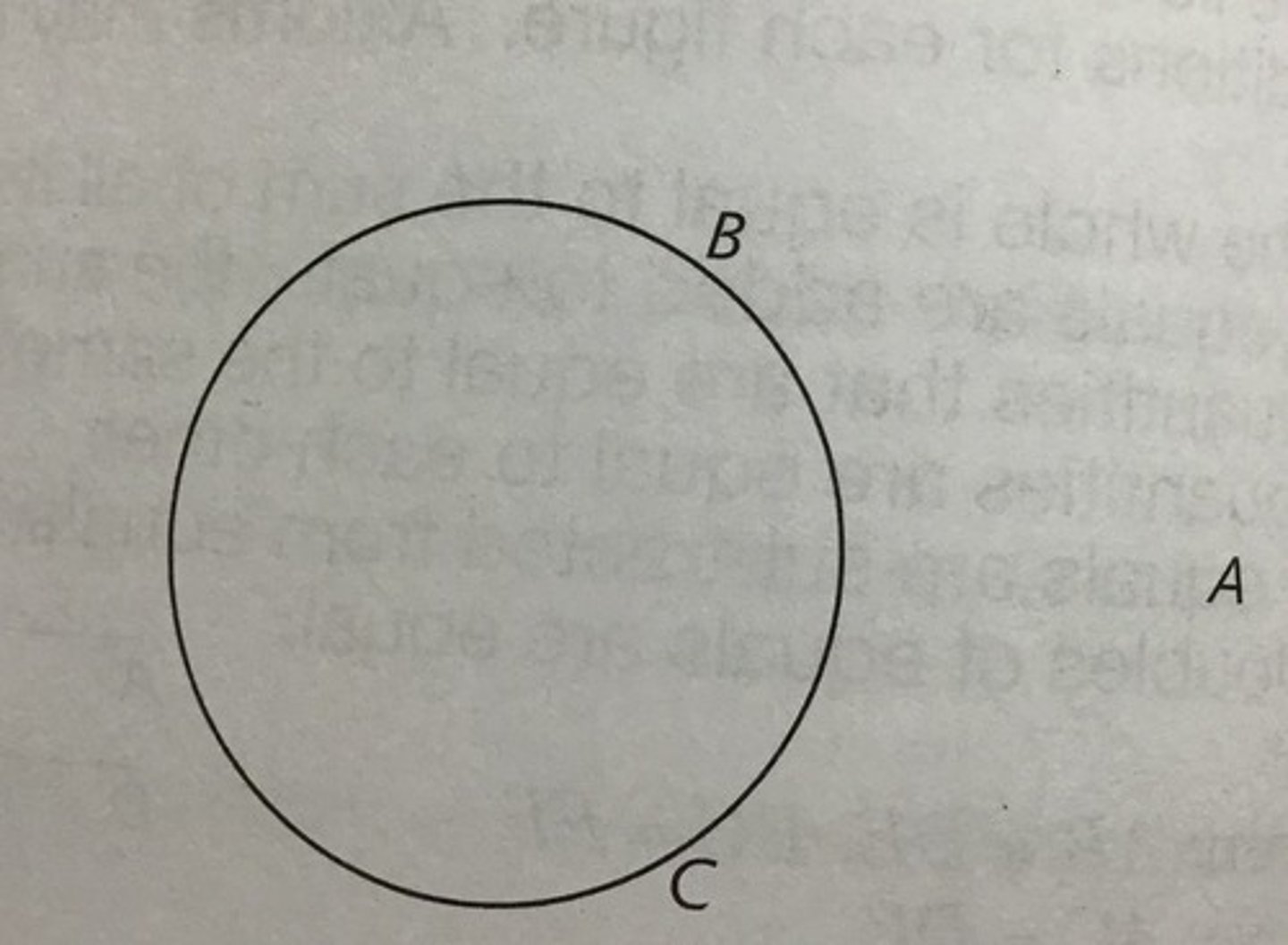
the whole is equal to the sum of all its parts

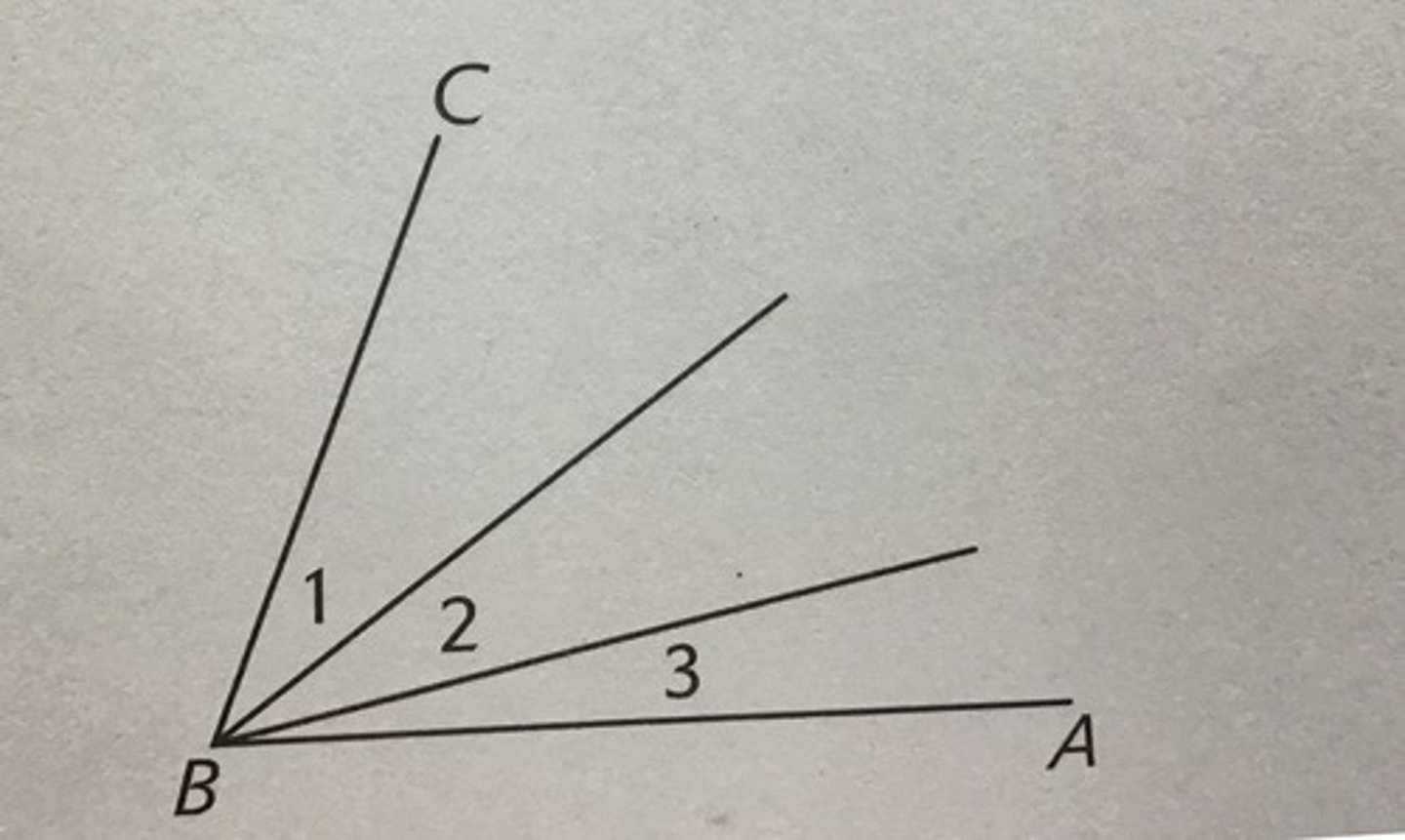
Given: Angle 1 and Angle 2 and Angle 3

Prove: Angle ABC = Angle 1+ Angle 2+ Angle 3

quantities that are equal to the same quantity or equal quantities are equal to each other

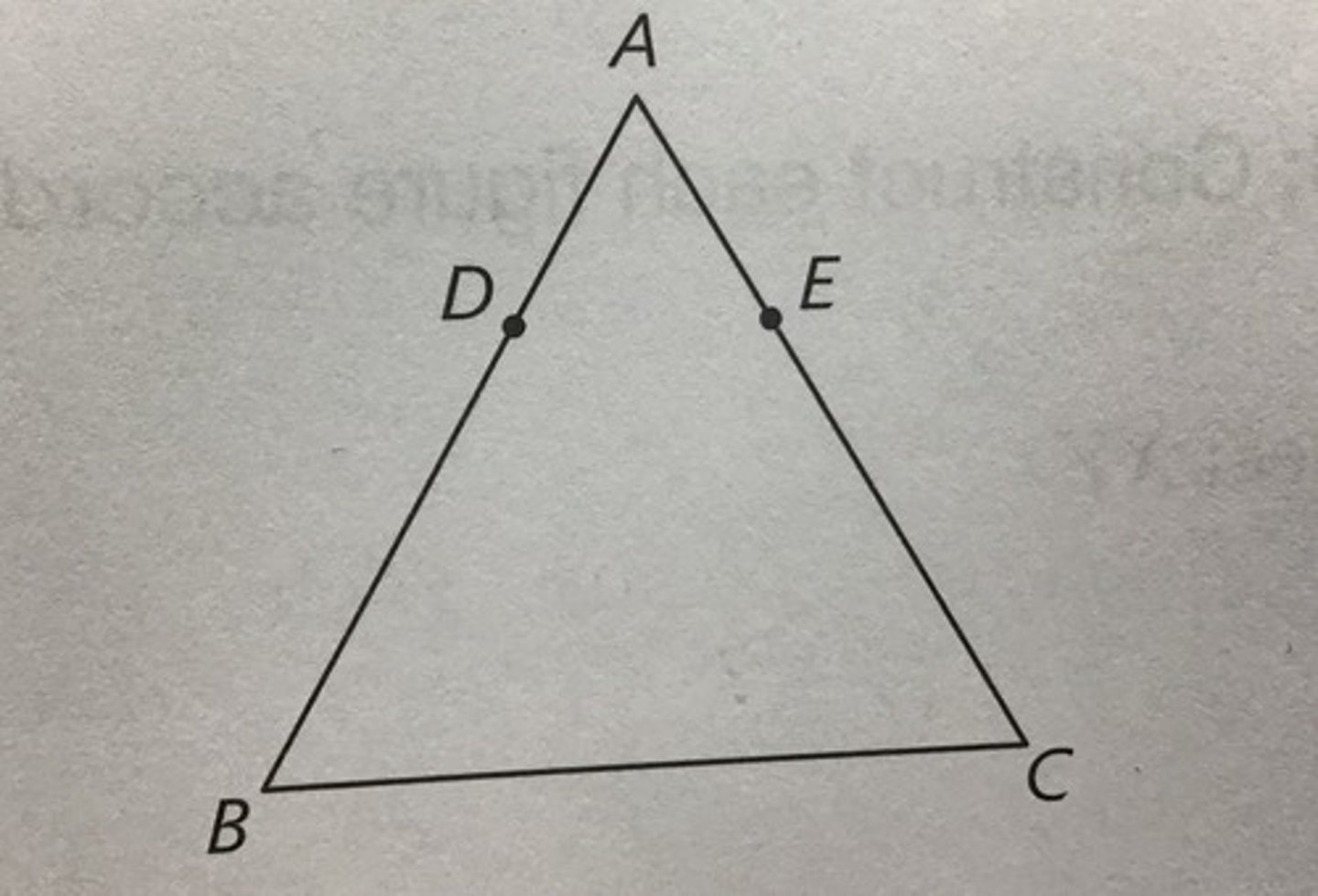
Given: AB= AD DC=AD

Prove: AB=DC

Doubles of equals are equal

Given: (all r angles) BCF=EDA ACF=FDA

Prove: Angle 1= Angle 2

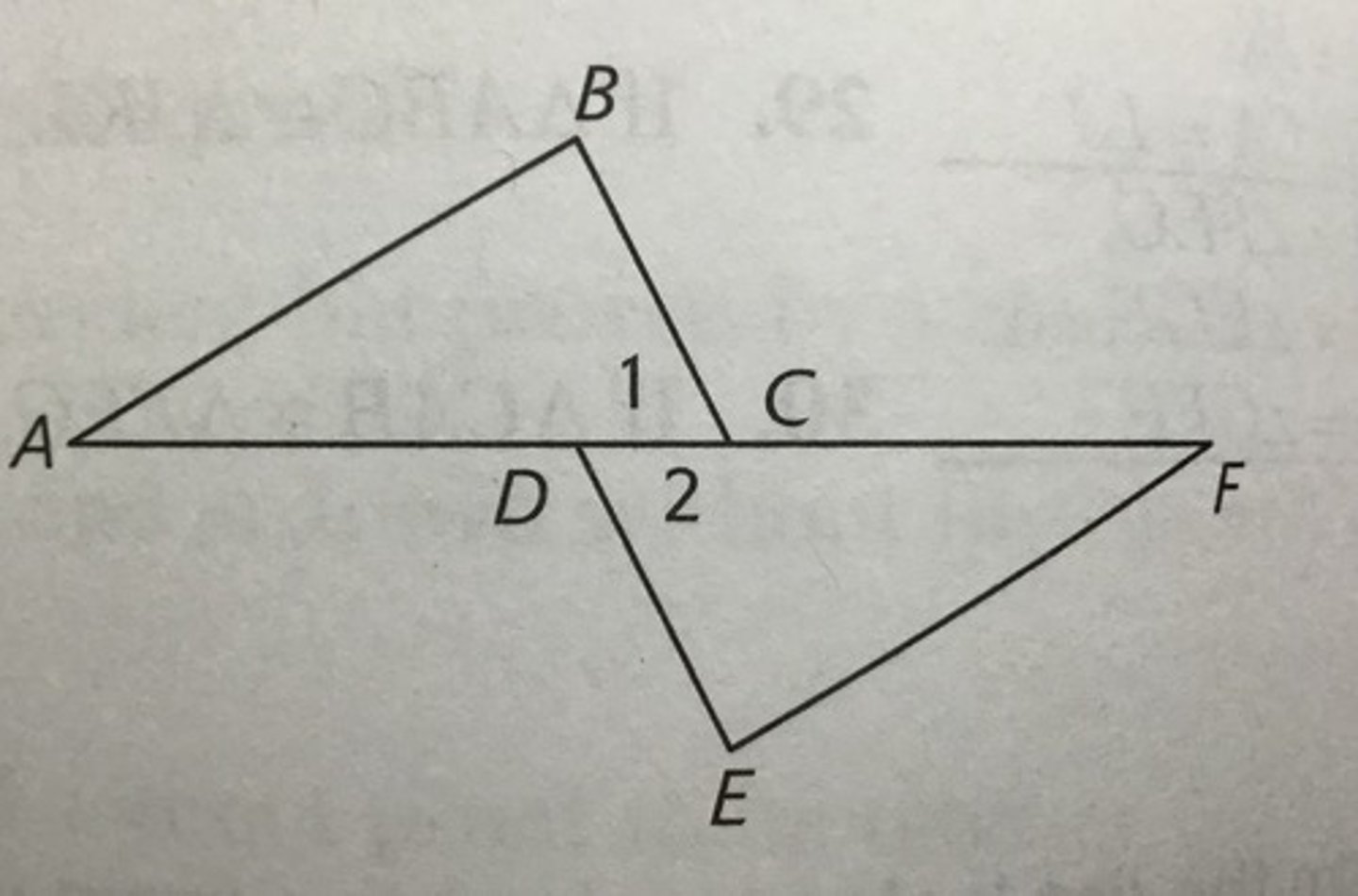
Quantites that are equal to the same quantity or equal quantities are equal to each other

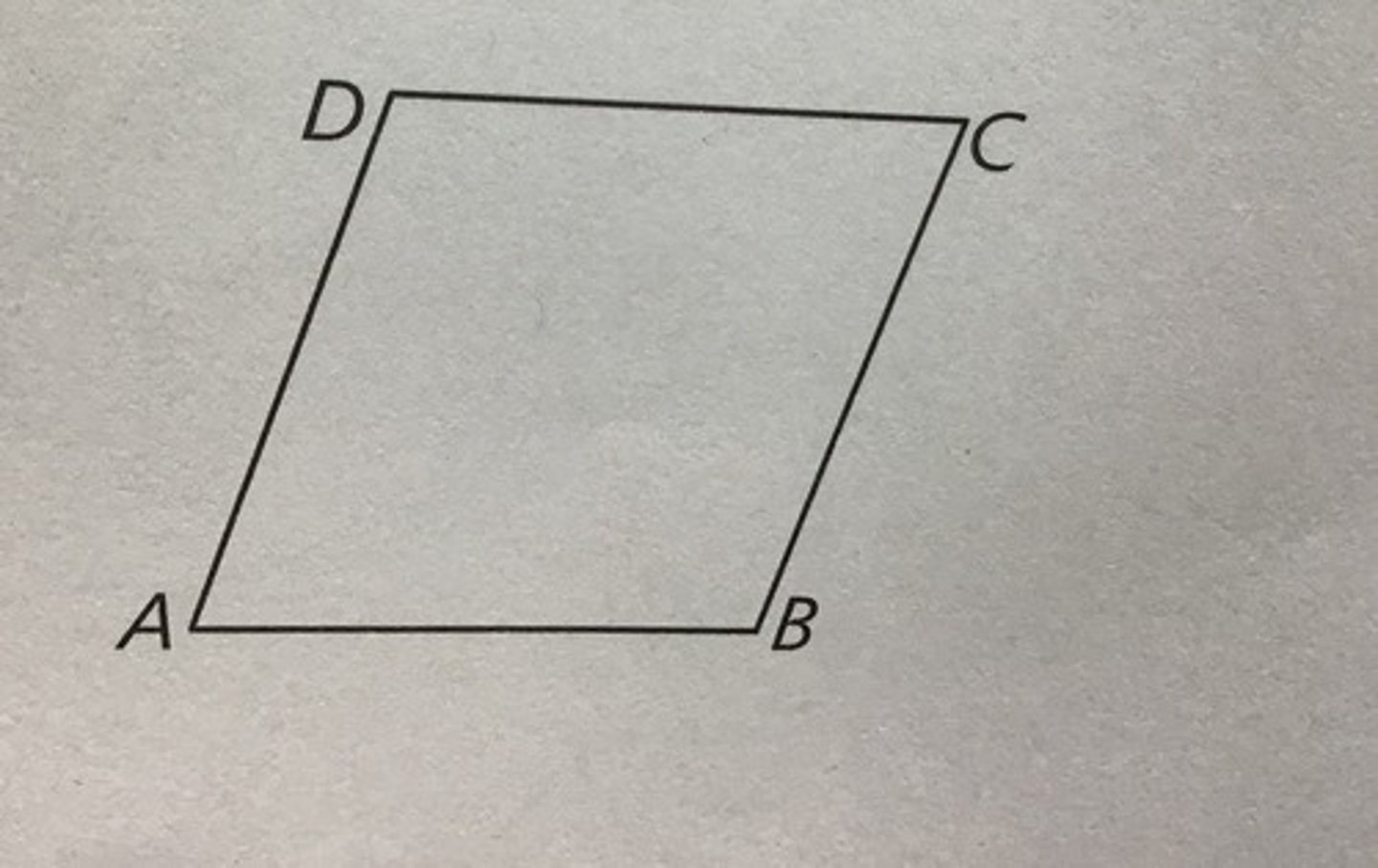
Given: AC=BC BC=BA

Prove: AC=BA