Bernoulli's Equation

kinetic energy

Fluid’s speed increases in a narrower channel, which gives the fluid an increase in ______________.

net work, gravitational

The increased kinetic energy comes from the ________ done on the fluid by the _____________ force.

net force, net force

A pressure difference occurs on the fluid when the channel narrows. This pressure difference results in a _________ on the fluids because P×A = F, and this ________ does the work

Wnet = (1/2)m(v)^2 - (1/2)m(v0)^2

Mathematical Representation of the Work-Energy theorem

The fast-moving stream of water and air lowers the pressure inside the shower, while outside pressure stays higher, pushing the curtain inward.

Why do shower curtains bulge inward when the shower is on?

High-velocity air between them lowers the pressure, while greater outside pressure pushes them together.

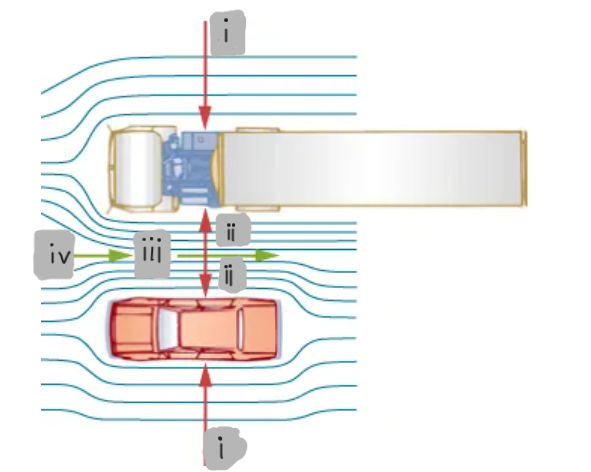
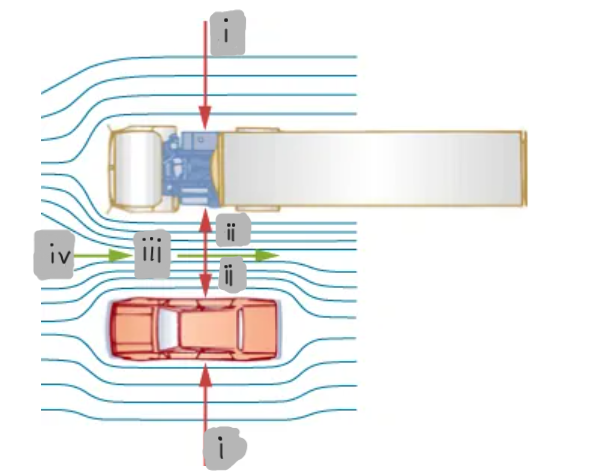
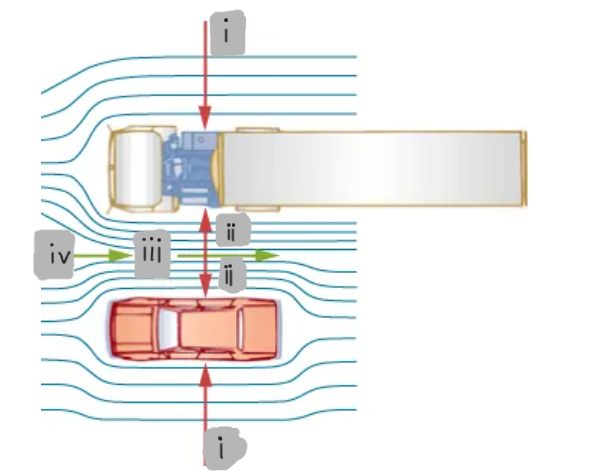
What causes a car and a truck to seem to pull toward each other when passing?

Trains passing in opposite directions tipped toward each other due to the low pressure between them.

What historical observation in the 1800s demonstrated this effect with trains?

Air speeds up (v2 > v1), lowering pressure inside (pi < p0)

In fluid dynamics, what happens to air speed and pressure in a narrower channel between vehicles?

Rapidly moving fluids create low-pressure regions; higher surrounding pressure pushes objects toward these regions.

What is the general principle connecting all the examples of shower curtains, cars, and trains?

p0

(i)

pi

(ii)

v2

(iii)

v1

(iv)

Conservation of Energy

Principle that gets applied to frictionless laminar flow

Bernoulli’s Equation

Name of the equation that shows us the relation between pressure and flow speed in a fluid

Daniel Bernoulli

A Swiss physician who came up with the Bernoulli’s Equation

Hydrodynamica

Work of Daniel Bernoulli that introduced his studies on fluid motions (was published in 1738)

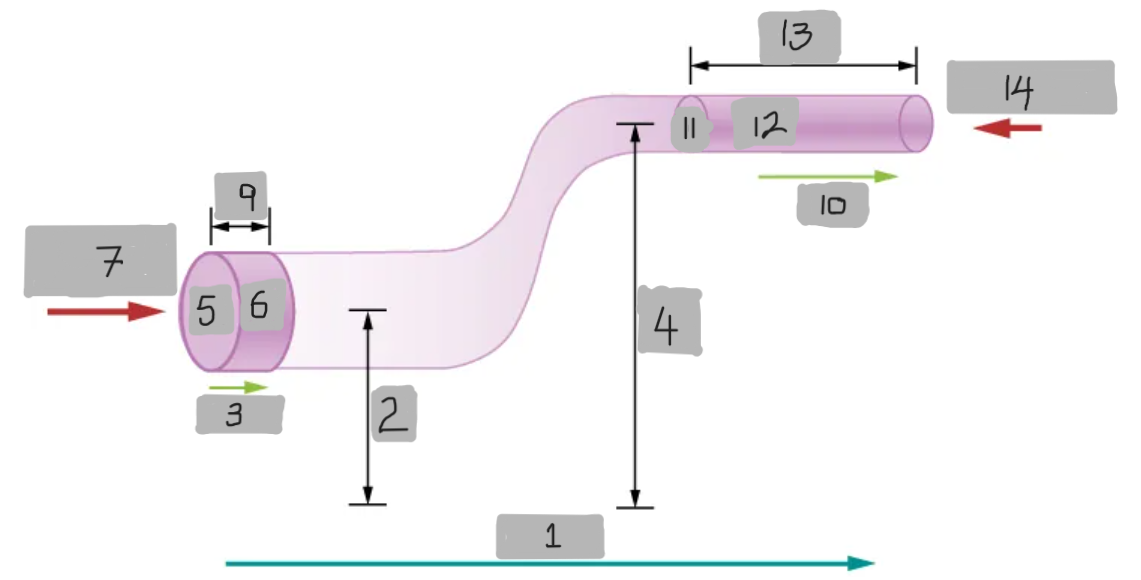
FLOW

(1)

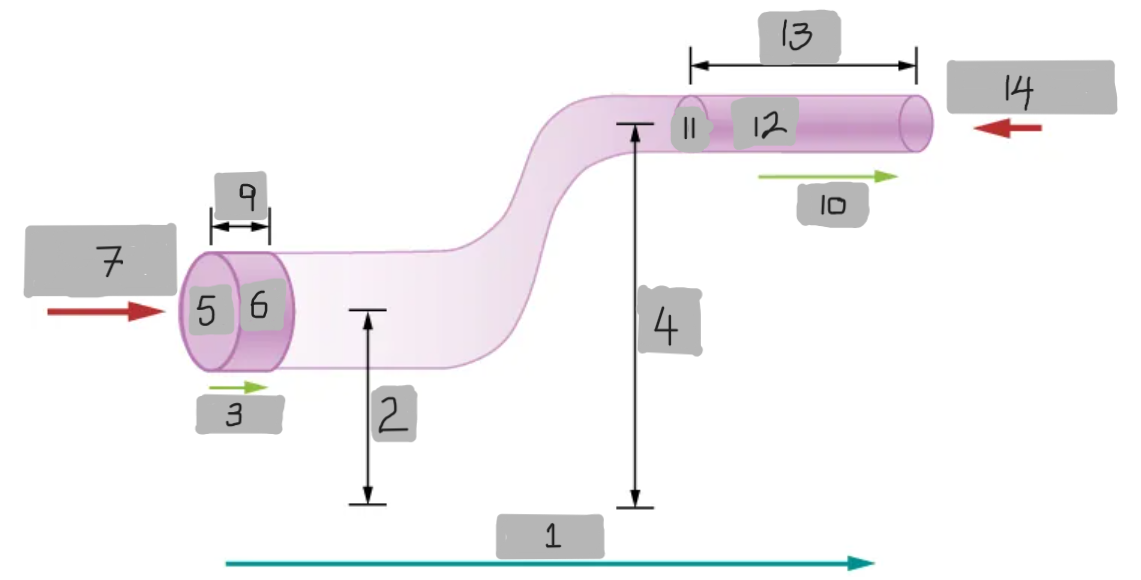
y1

(2)

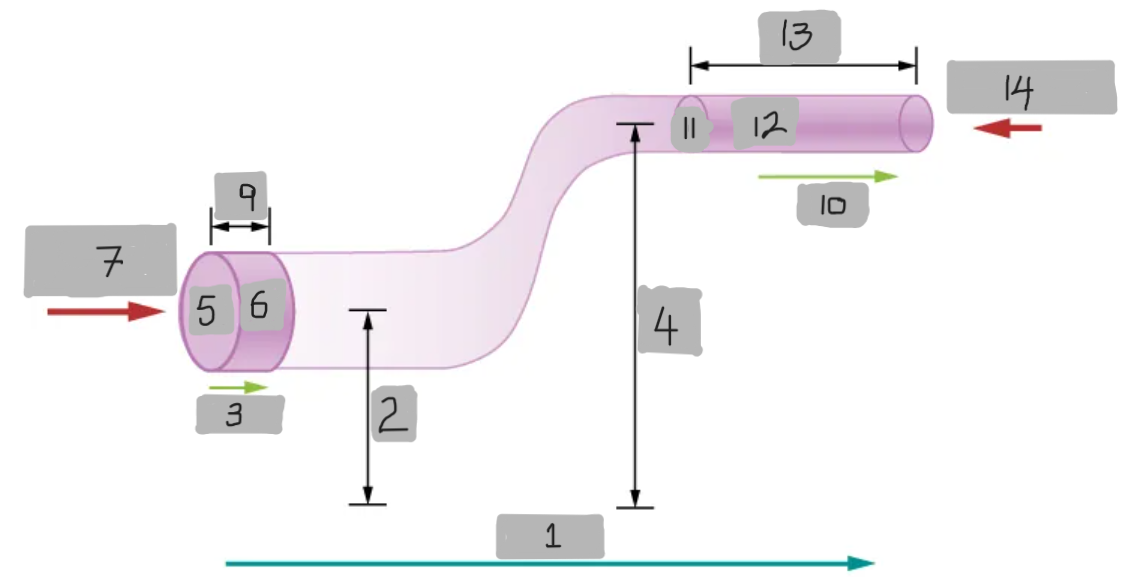
v1

(3)

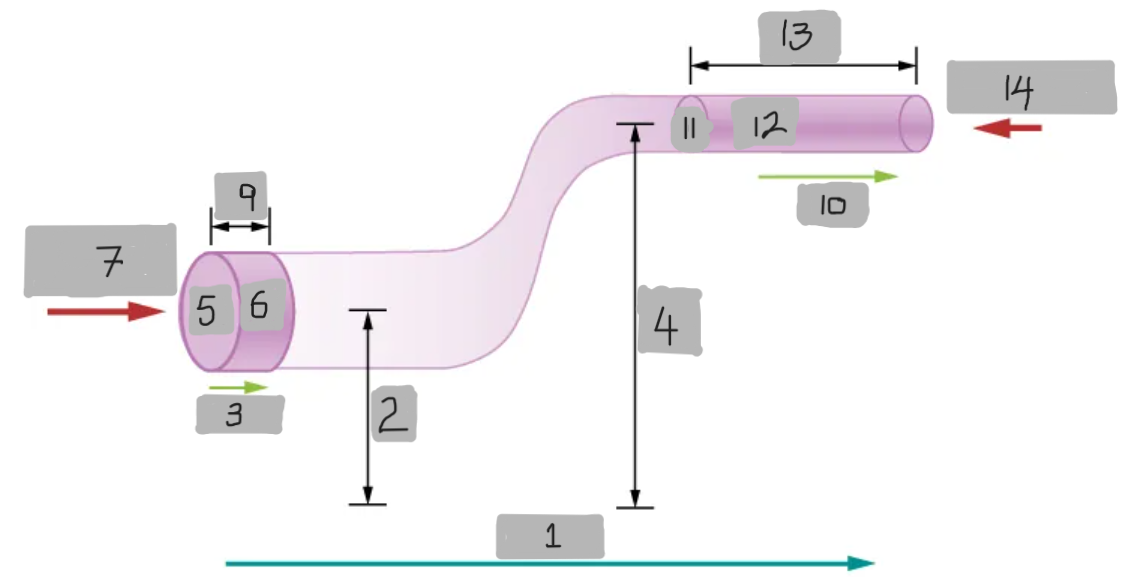
y2

(4)

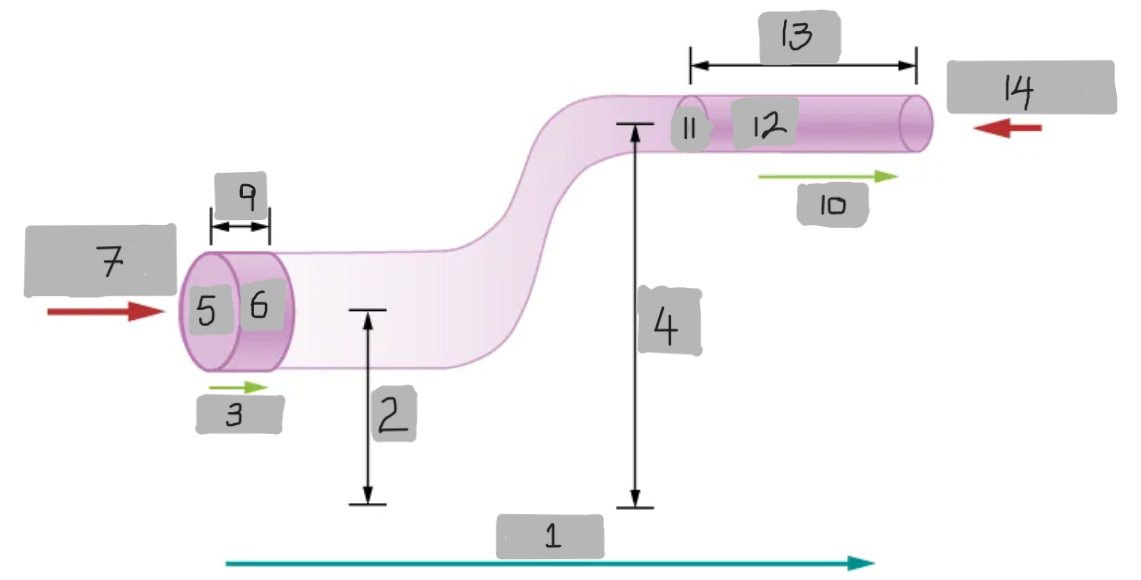
A1

(5)

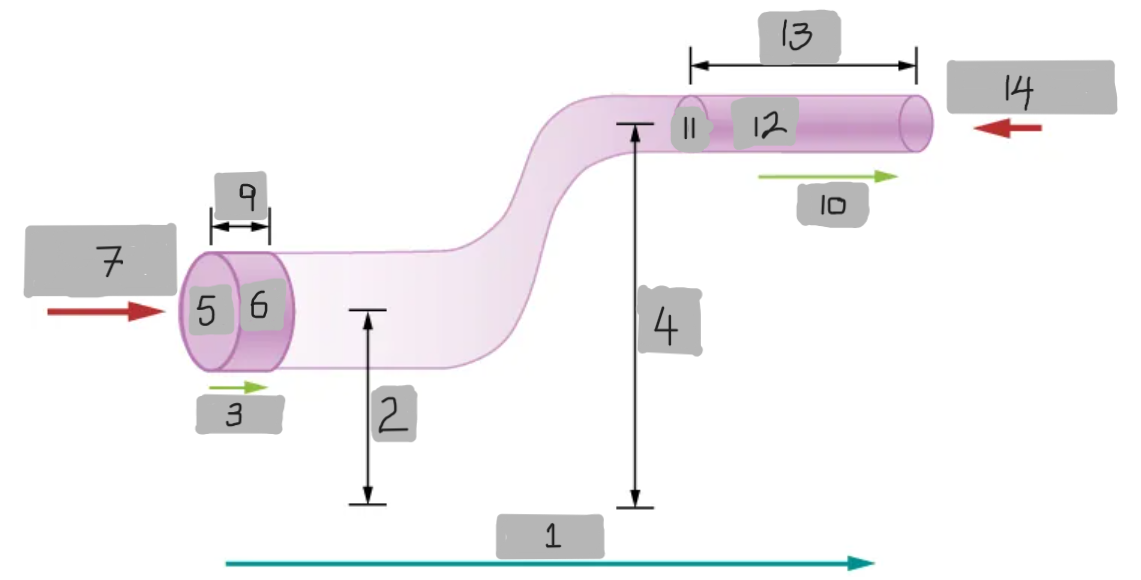
dV

(6)

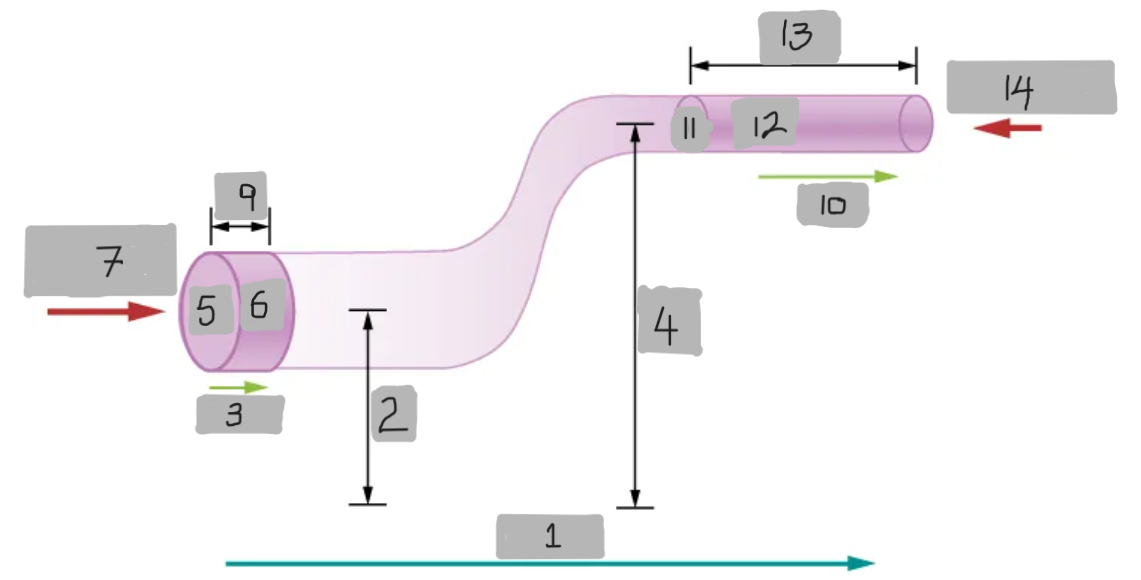
F1 = p1A1

(7)

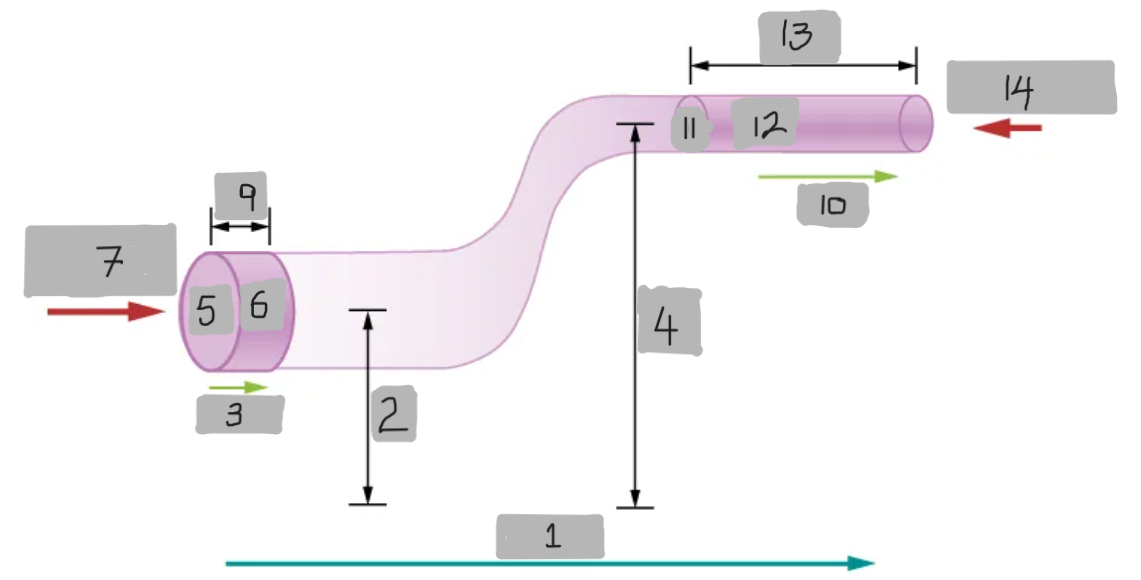
dx1

(9)

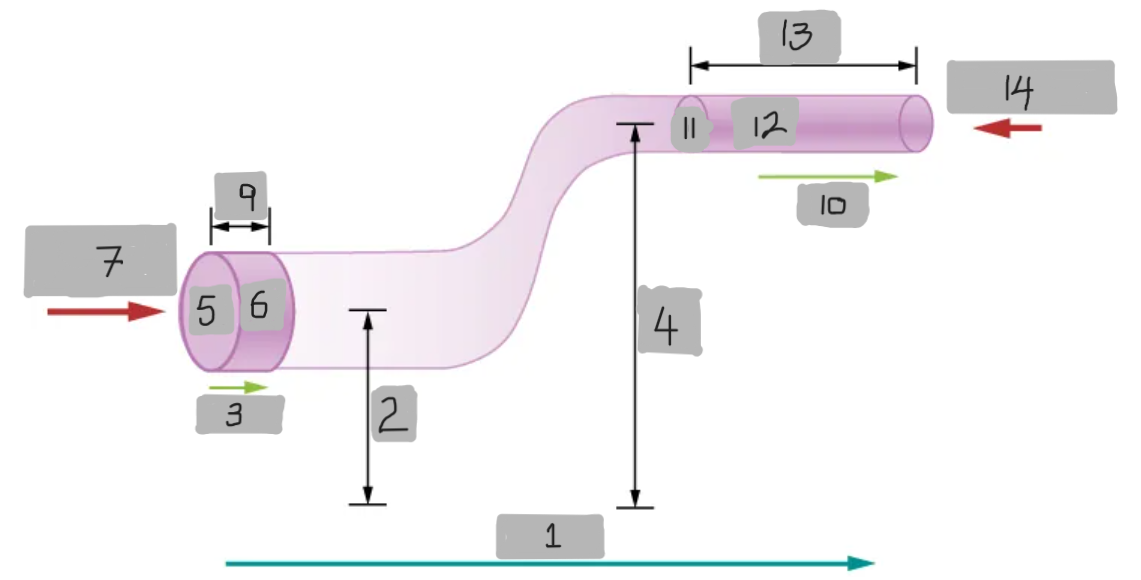
v2

(10)

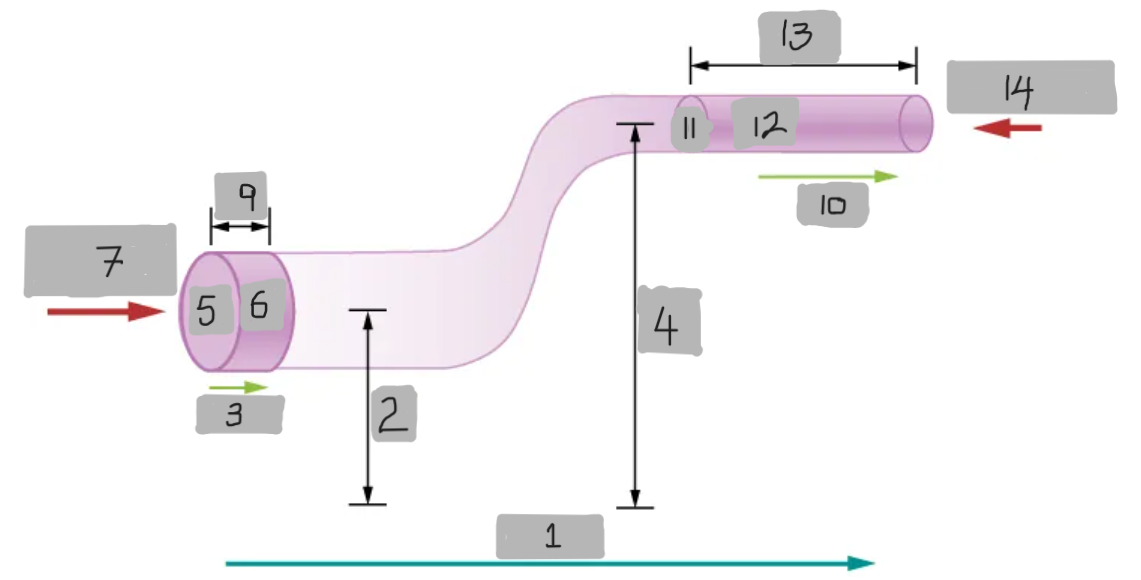
A2

(11)

dV

(12)

dx2

(13)

F2 = p2A2

(14)

Density of the fluids at the two points is the same

First assumption of the Bernoulli’s geometric model

Because the fluid is incompressible

Why are we saying that the shaded volumes inside the Bernoulli’s geometric model are the same?

There are no viscous forces inside the fluid, so the energy of any part of the fluid will be conserved

Second assumption of the Bernoulli’s geometric model

dW = F1dx1 - F2dx2

The very first equation, which is written to calculate the work that was done on the fluid, in order to derive the Bernoulli’s equation.

dW = p1A1dx1 - p2A2dx2 = p1dV - p2dV = (p1 - p2)dV

Derivation of the very first equation to be written in only in the terms of pressure and the rate of change in the volume.

conservative force, kinetic energy

The work done inside the Bernoulli’s geometric model was due to the __________________ of gravity and the change in the ______________ of the fluid.

dK = (1/2)m2(v2)^2 - (1/2)m1(v1)^2 = (1/2)ρdV((v2)^2 - (v1)^2)

Mathematical representation of the change in the kinetic energy of the fluid inside the Bernoulli’s geometric model (with its derivation)

dU = mgy2 - mgy1 = ρdVg(y2 - y1)

Mathematical representation of the change in the potential energy of the fluid inside the Bernoulli’s geometric model (with its derivation)

dW = dK + dU

Mathematical representation of the energy equation of the fluid inside the Bernoulli’s geometric model

(p1 - p2)dV = (1/2)ρdV((v2)^2 - (v1)^2) + ρdVg(y2 - y1)

The energy equation of the fluid inside the Bernoulli’s geometric model. (This time the Mathematical definitions of dU, dK, and dW are substituted)

(p1 - p2) = (1/2)ρ((v2)^2 - (v1)^2) + ρg(y2 - y1)

The energy equation of the fluid inside the Bernoulli’s geometric model where the definitions of the dU, dW, and dK were substituted. (This time the equation is simplified)

p1 + (1/2)ρ(v1)^2 + ρgy1 = p2 + (1/2)ρ(v2)^2 + ρgy2

The energy equation of the fluid inside the Bernoulli’s geometric model where the definitions of the dU, dW, and dK were substituted. (This time the equation is simplified and rearranged)

The mechanical energy of any part of the fluid changes because of the work done by external fluid forces, caused by varying pressure along the flow.

What does Bernoulli’s relation state about the mechanical energy of a fluid?

Bernoulli’s Relation (Energy Change)

Mechanical energy in a fluid change due to work from pressure differences along the flow.

p + (1/2)ρv^2 + ρgy = constant

Bernoulli’s equation but written generally as a “conservation principle along the flow” because the two points here are chosen arbitrarily;
Stating that the combination of pressure and the sum of kinetic and potential energy densities is constant not only over time, but also along a streamline.

Frictionless and Incompressible

Bernoulli’s equation will be valid for the fluids that have the two following properties.

Yes. At the same height, pressure can vary if different parts of the fluid have different flow speeds.

In a dynamic fluid situation, can pressures at the same height differ? If so, Why?

Individual quantities may change, but the total energy remains constant, due to the(conservation of energy for an incompressible, frictionless fluid).

What does Bernoulli’s equation state about the total energy of a small fluid volume along its path?

3

How many terms are there inside the General form of Bernoulli’s equation, that gets broadly applied to the incompressible and frictionless fluid?

Pressure term

p → (Represents the static pressure exerted by the fluid)