Geo U8 - Similar Figures

U8: 2 figures are similar if and only if

- corresponding angles are congruent

-corresponding sides are proportional (have equal ratios)

U8: ~

"Is similar to"

When used with shapes the vertices should be in corresponding order

(Order matters) —> corresponding verticies in the same “position”

△ABC~△DEF

would be a similarity statement read "triangle ABC is similar triangle DEF"

U8: How do you do cross multiplication and why does it work? And, what's another way to say this in terms of extremes

A/b=c/d —> bc=cd and then divide by c

Basically: multiply across and then divide the last number which is the value of the variable

The product of the means is equal to the product of the extremes: ad=bc

Extremes: highest and lowest

Means: the other numbers

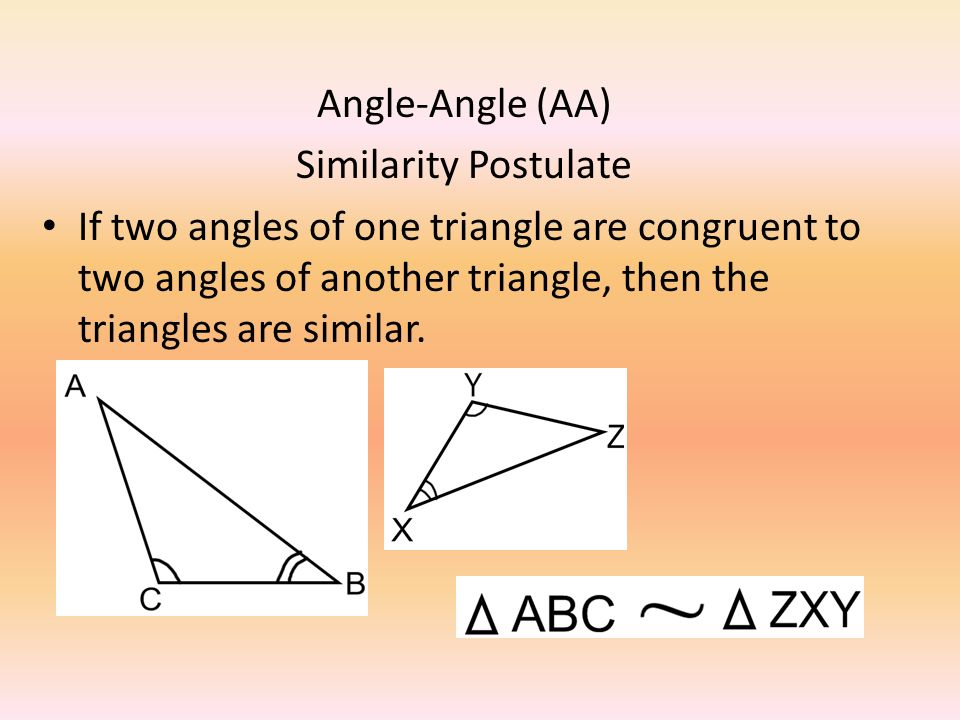
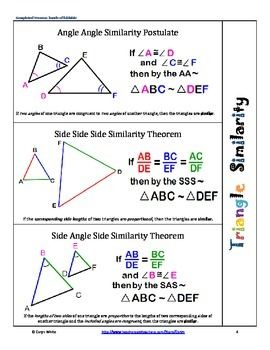
U8: Angle-Angle Similarity Postulate

If two angles of one triangle are congruent to two angles of another triangle, then the two triangles are similar.

NOTE: THIS CAN ONLY BE USED FOR TRIANGLES NOT ANY OTHER POLYGON

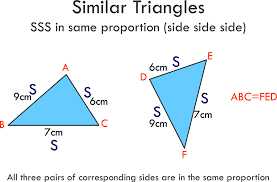
U8: Side-Side-Side Similarity Theorem

If three pairs of corresponding sides of two triangles are PROPORTIONAL (in the same ratio) then the triangles are similar.

U8: Side-Angle-Side Similarity Theorem

If two pairs of corresponding sides of two triangles are proportional and the included angles are congruent, then the triangles are similar

U8: Can we do a ratio without proving the triangles are first similar?

NO!

We must first conclude two triangles are similar before solving a ratio (between corresponding sides)

U8: What are the five ways to prove triangles are similar

AA, SAS, and SSS

Yes, AAS works or AAA works because it's effectively the same as AA (Angle-Angle)

U8: Arithmetic mean

If we add the same number what are the missing terms?

Average of the two other variables (middle number of the average)

A , A+B)/2, B

ex: 2,5,8 and 6,14,22 and a,

(A+B)/2

U8: Geometric mean

If we multiply by the same number what is the missing term?

a, √ab , b

Ex: 2,4,8 and 5,10,20 and 6,18,54

Because: √b/a is equal to √ab

U8: If the sides lengths of a polygon are multiplied by n: (perimeter and area)

The perimeter becomes n times longer

The area becomes n^2 times longer

U8: Ratios for similar figures (sides, perimeter, area)

Sides : a:b

Perimeter: a:b

Area: a^2:b^2

U8: How to solve similar right triangles

Draw three triangles in the same direction with the right angle on the bottom. Label each triangle (large, medium, small) with the hypotenuse, small leg, and large leg. Corresponding sides can be written into proportions.

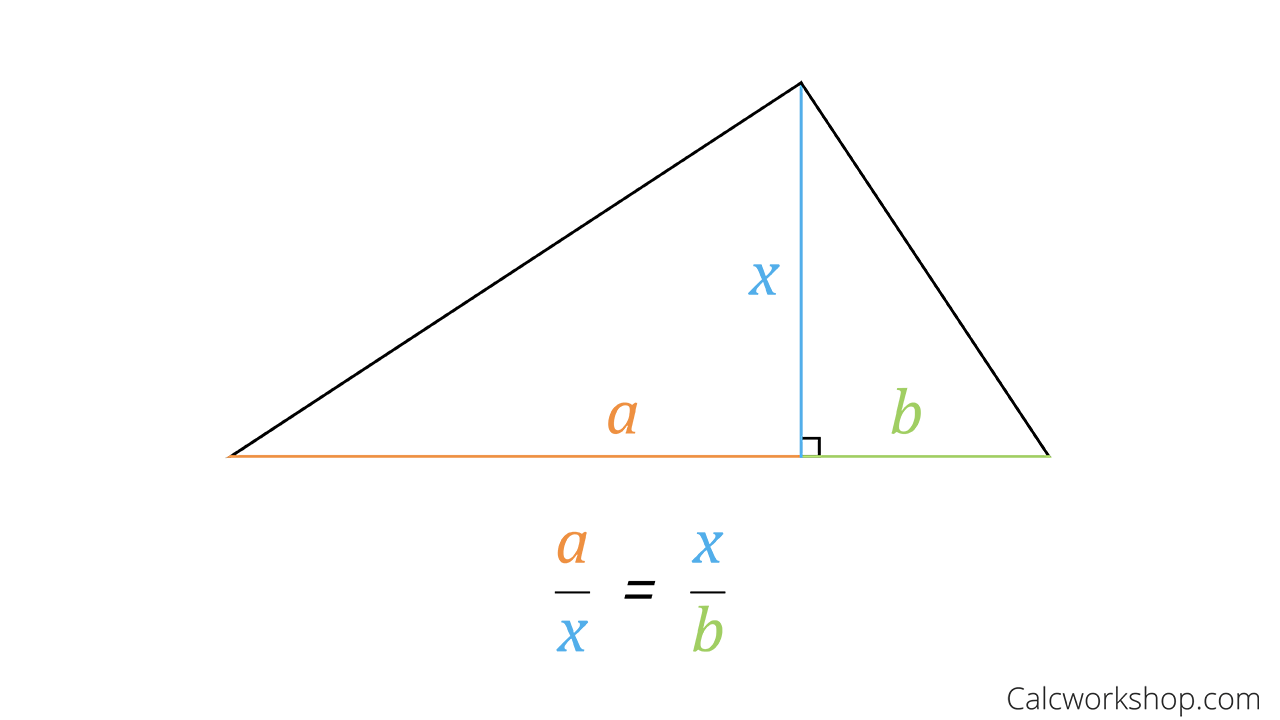
U8: Why are similar right triangles similar?

Label the right angle meaning the other angle is x, leaving the last angle to be 90-x

The other triangle (on the left) must also have a right angle adjacent to the other right angle. This leaves the other angle 90-x and x. These angles are the same (congruent) meaning the triangles are SIMILAR. Thus, we can set up proportions for corresponding sides.

U8: Proving the angle bisector theorem

Construct an auxiliary line parallel to the mid segment and then extend one of the sides.

Use the triangle proportionality theorem and the isosceles triangle theorem converse. Then definition of congruent and substitution property of equality.

(Review/practice for a better understanding)

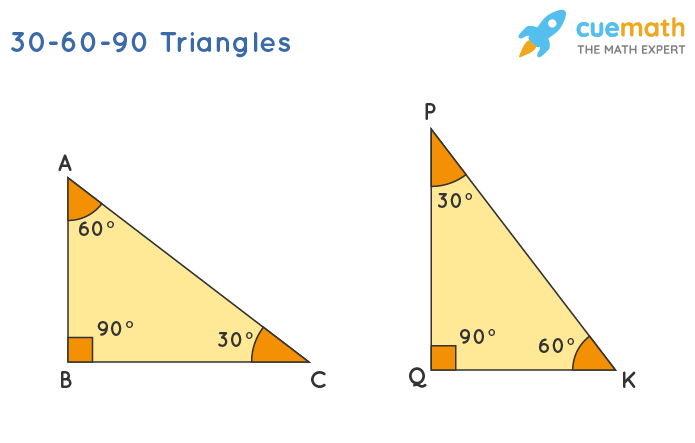
U8: 30-60-90 triangle

x= short leg

x√3 = height/long leg

2x = hypotenuse

Half a equilateral

Think of what an angle bisector does and then you can use pythagreom theorem

U8: 45-45-90 triangle

Half a square also a right isosceles triangle

x = one leg

x = one leg

x√2 =hypotenuse

Sides are the same because it's half a square. The opposite angles are 45 and congruent because of the isosceles triangle theorem converse.

To get from the leg to the hypotenuse we multiply by √2

To get from the hypotenuse to the leg we divide by √2

Hypotenuse = leg times radical 2

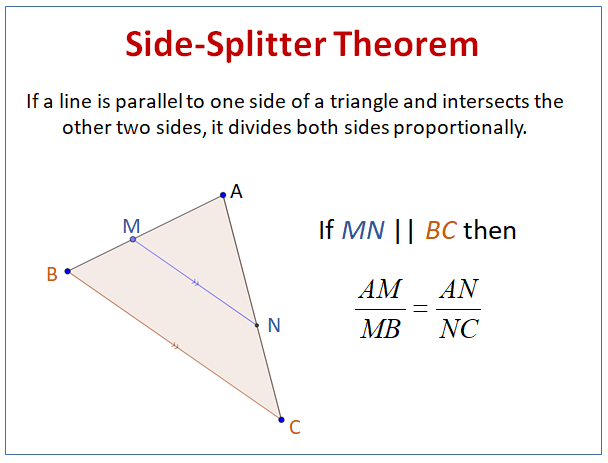
U8: Triangle proportionality theorem (side splitter theorem)

If a line parallel to one side of a triangle intersects the other two sides of the triangle then the line divides these two proportionally

The small side on the left over the larger side on the left

The small side on the right over the larger side on the right

(Not over the WHOLE side just the two parts of each other, smaller over larger)

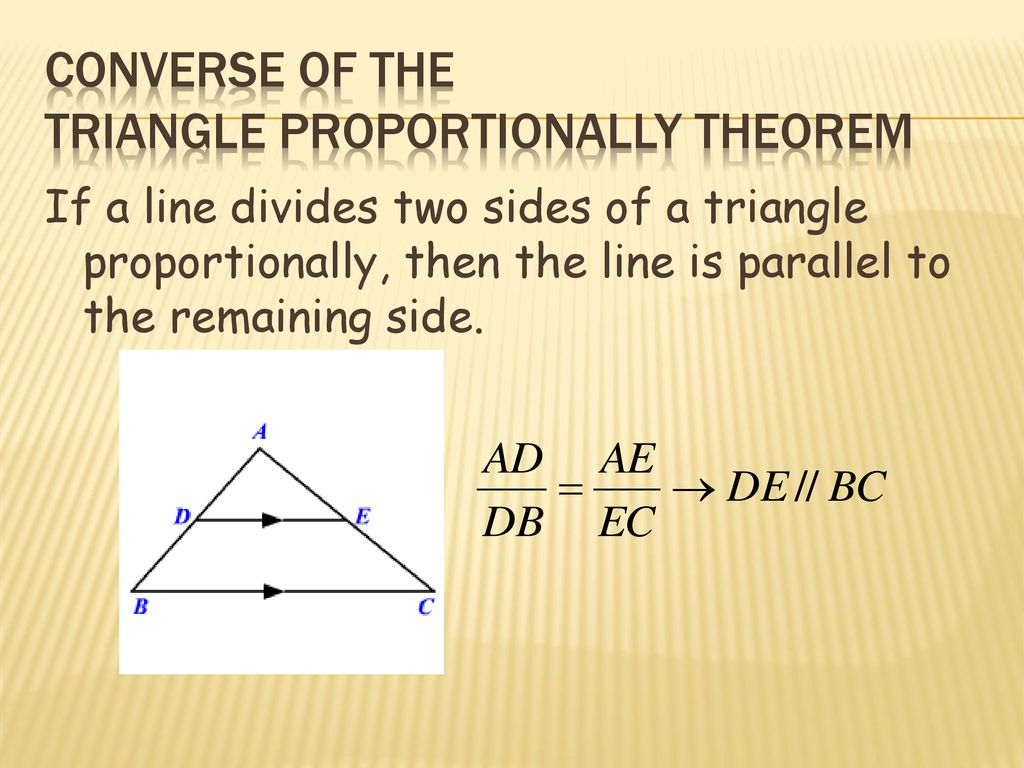
U8: Triangle Proportionality (Side-Splitter) Converse

If a line intersects two sides of a triangle and divides these sides proportionally, the line is parallel to the third side of the triangle. (This is because the triangle are similar because of the SAS similarity theorem, making corresponding angles congruent)

U8: See 2 polygons similar? There are four possibilities...

- __ ~__ because corresponding angles are congruent and corresponding sides are proportional x/x = y/y (show equal ratios)

- the polygons are not similar because corresponding angles are not congruent ∠≆∠

- the polygons are not similar becuase corresponding sides are not proportional x/x ≆ y/y

- We do not have enough information (about sides or angles)

U8: Rationalizing the denominator

multiply the numerator and denominator by the radical currently in the denominator then simplify

This makes it rational because there isn't a radical in the denominator

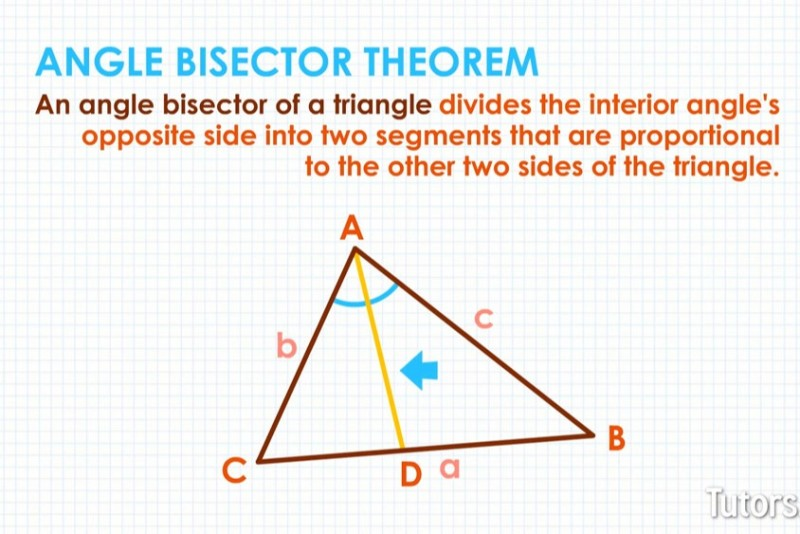
U8: Angle Bisector Theorem

If a ray bisects an angle of a triangle, it divides the opposite side into segments that are proportional to the adjacent sides.