Geo U3 - Polygons and Parallel Lines

U3: Isosceles Triangle

At least 2 sides are congruent

-2 congruent base sides called legs

-the third side is called the base (between 2 congruent base angles)

• An equilateral triangle can also be calcified as an isoceles triangle because it has “at least” two congruent angles/sides

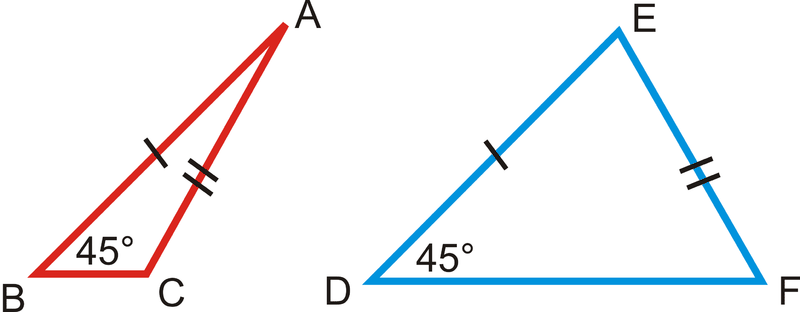
U3: Two conjectures you can make about isosceles triangles?

Isoceles Triangle Theorem

If two sides of a triangle are congruent then the angles across from those sides are congruent

If two angles of a triangle are congruent then the sides across from those angles are congruent

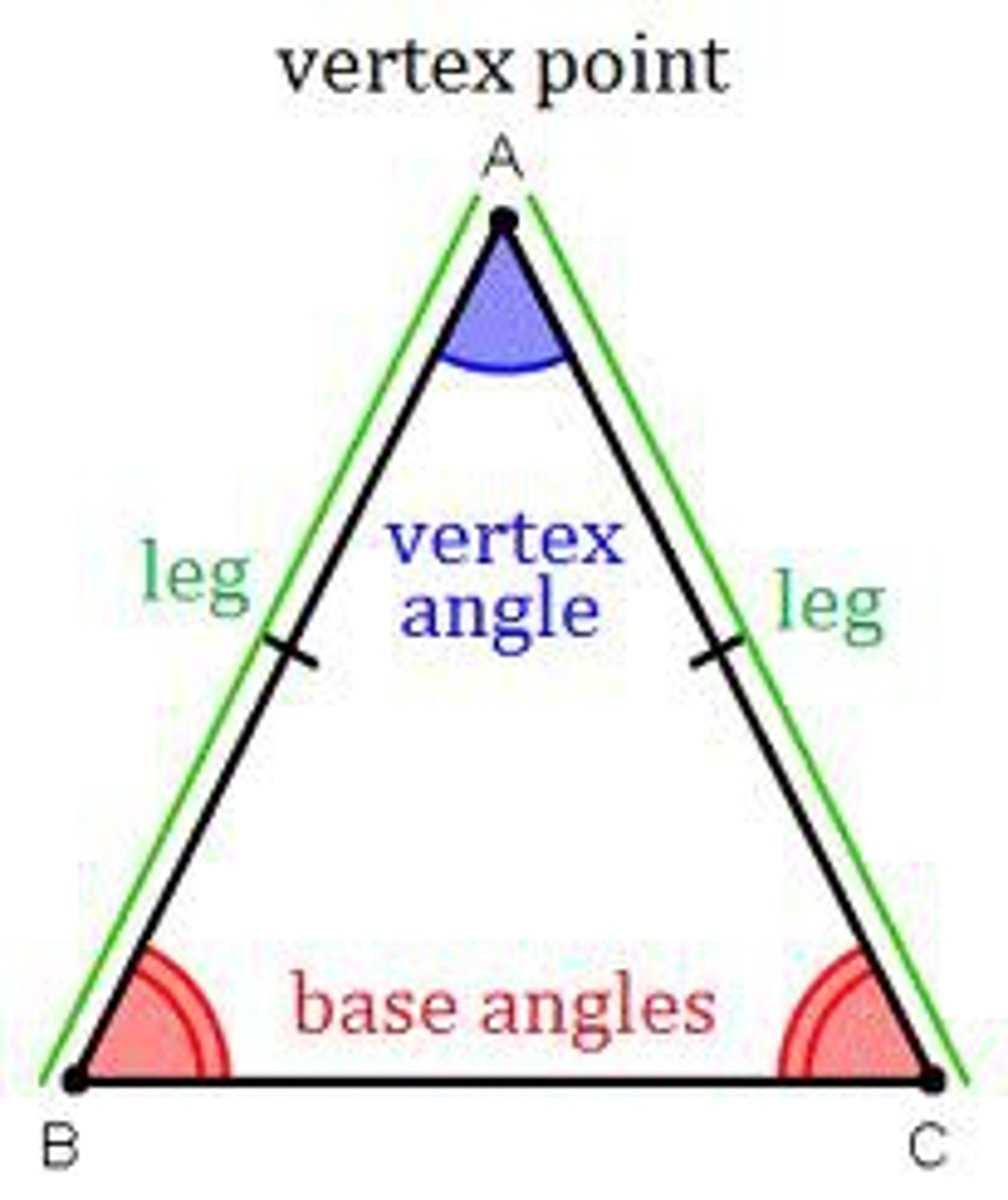
U3: vertex angle of an isosceles triangle and base angle of isoceles triangle

Vertex angle: the angle formed by two congruent sides (angle that doesn't have another angle congruent, the top bit)

Base angle: the angles that are congruent to eachother (not always on the bottom of the triangle)

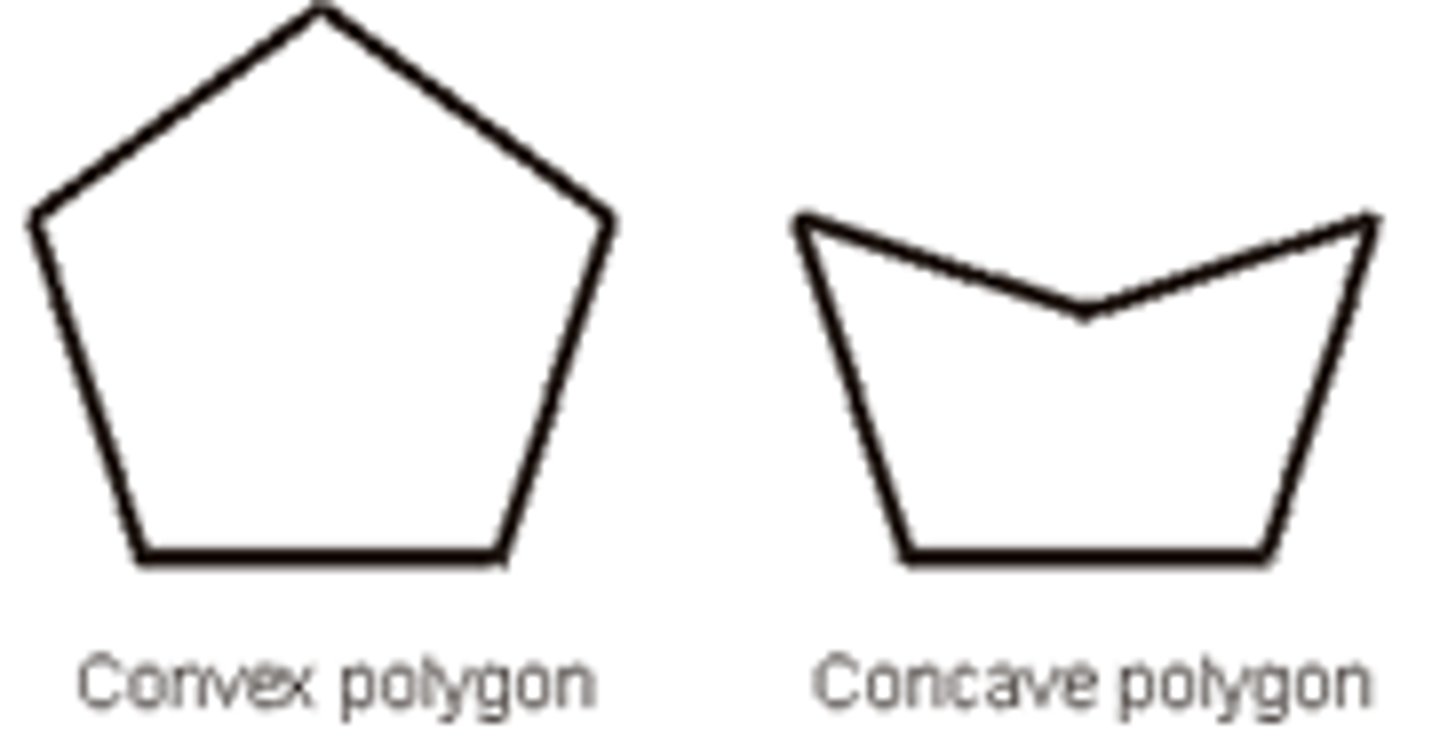
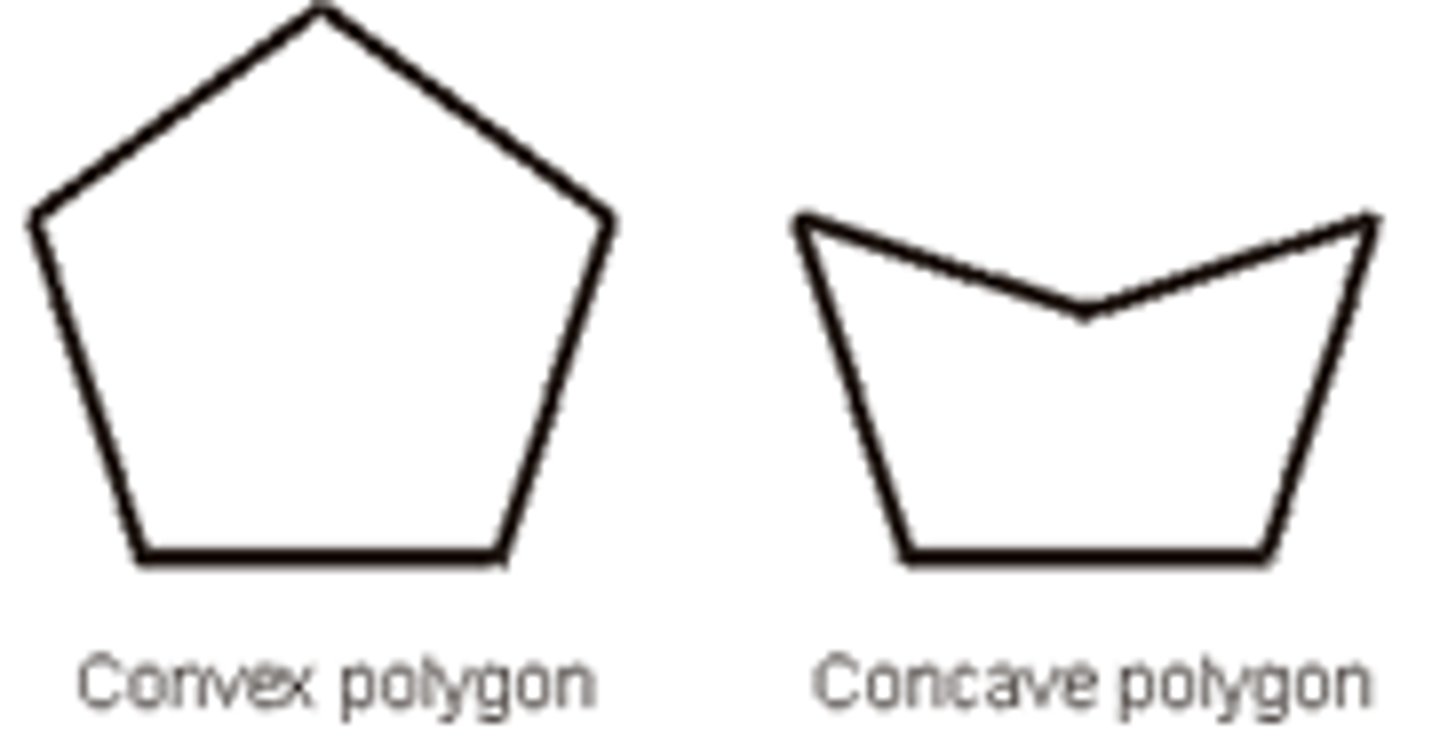
U3: Convex Polygon

A polygon is a convex if and only if...

-it contains all the line segments connecting any pair of points

-each interior angle is less then 180 (no reflexive interior)

-otherwise it is concave

-turn in way

U3: Exterior angle

-the supplement of an interior angle of a polygon

-must form a line (straight) with the interior angle

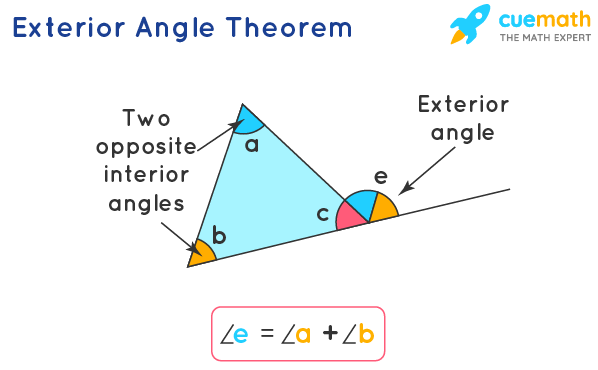
U3: Exterior angle theorem (and how to prove)

The exterior angle theorem states that when a triangle's side is extended, the resultant exterior angle formed is equal to the sum of the measures of the two opposite interior angles of the triangle. The theorem can be used to find the measure of an unknown angle in a triangle.

In this image: Angle e = angle b + angle a

How to prove:

A+b+c=180 interior angles sum of triangles

C+d=180 a straight angle is 180

A+b+c=c+d transitive prop equality

A+b= d subtraction prop of equality

U3: Concave Polygon

-we can draw a segment between any two points OUTSIDE a polygon

-can contain interior reflex angles

-turn more then one way

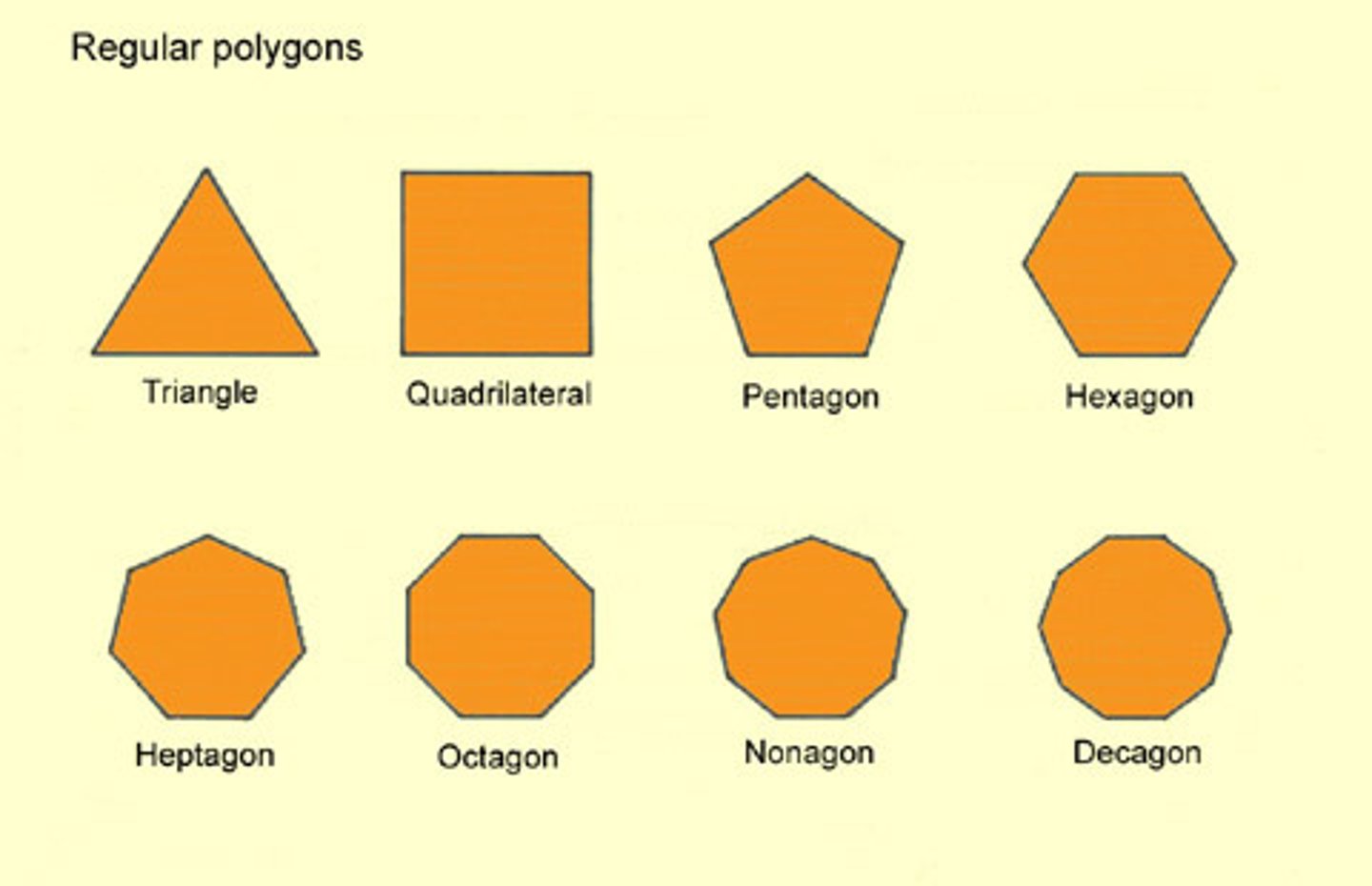
U3: Regular Polygon

all sides are congruent and all angles are congruent

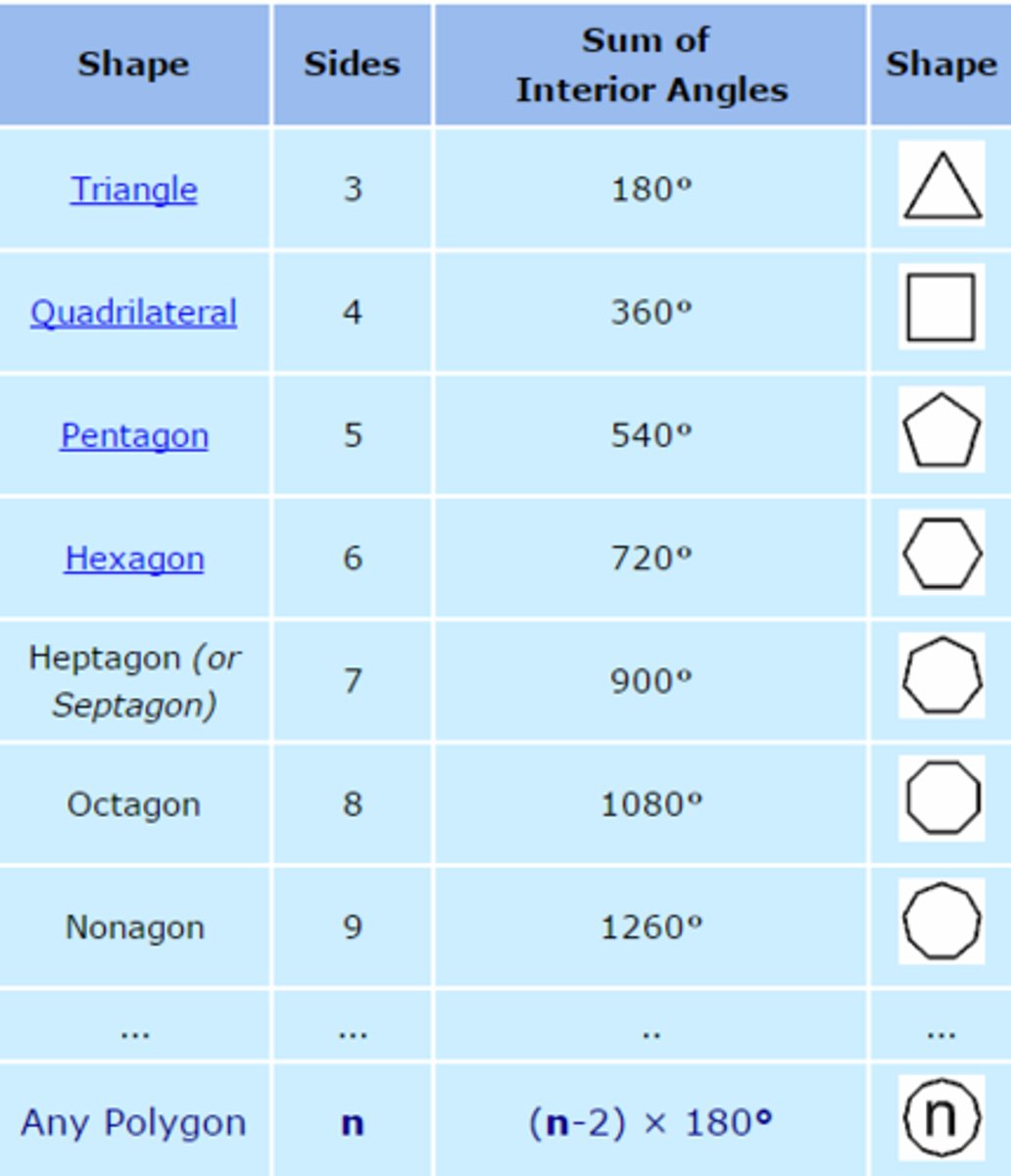
U3: Equation for the sum of interior angles of a polygon (n=number of sides)

(n-2)180

Or all angles - 360 (all angles is n x 180 for all triangles)

U3: Equation for each interior angle

(n-2)180 divided by n

U3: Equation for (each) exterior angle measure and why

360/n

- because 180- ((n-2)180))\n to find supplementary of each interior angle

U3: Transitive property of equality or congruence

If a=b and b=c, then a=c

• different than substutiton because it is between three things/numbers/figures

U3: Name the names of shapes with sides 3-10

3- triangle

4- Quadrilateral

5- pentagon

6- hexagon

8- octagon

10- decagon

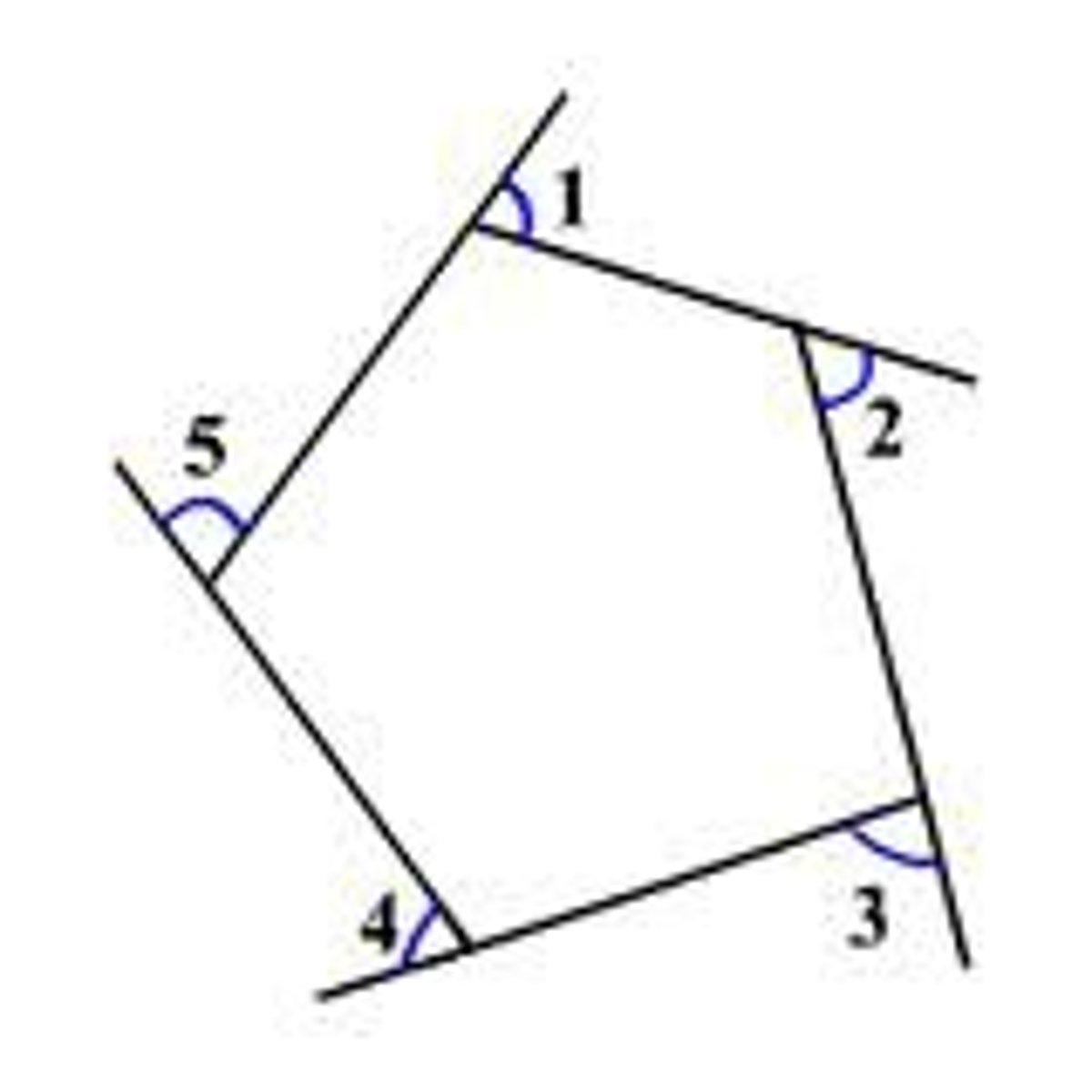
U3: Equation for the sum of exterior angles of any polygon

a + b + c + d = 360

The sum of exterior angles of ANY polygon equal 360

U3: Polygon

A plane figure with at least three straight sides and angles, typically five or more.

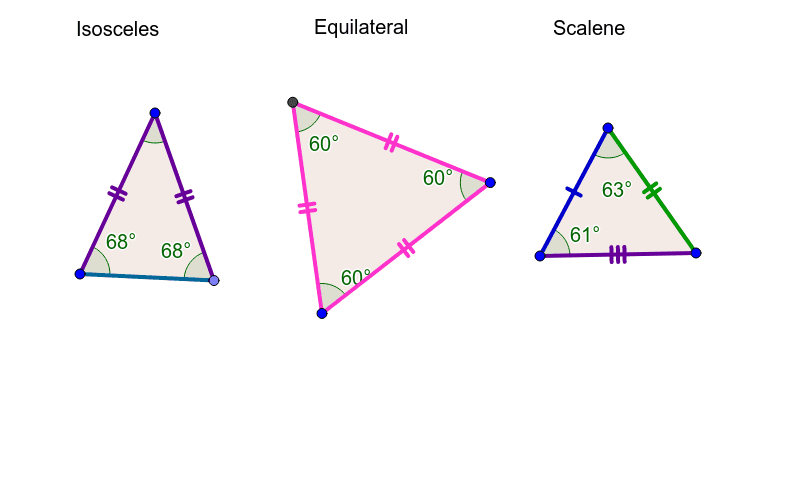
U3: Scalene Triangle V Equilateral V Isoceles

Scalene: All different side lengths and different angle measures

Equilateral: All angles are congruent, all side lengths are congruent

• also considered a isoceles because it has “at least” two congruent angles

Isoceles: “at least” two angles are congruent, opposite angles and sides are congruent (has a base angles, and vertex angles)

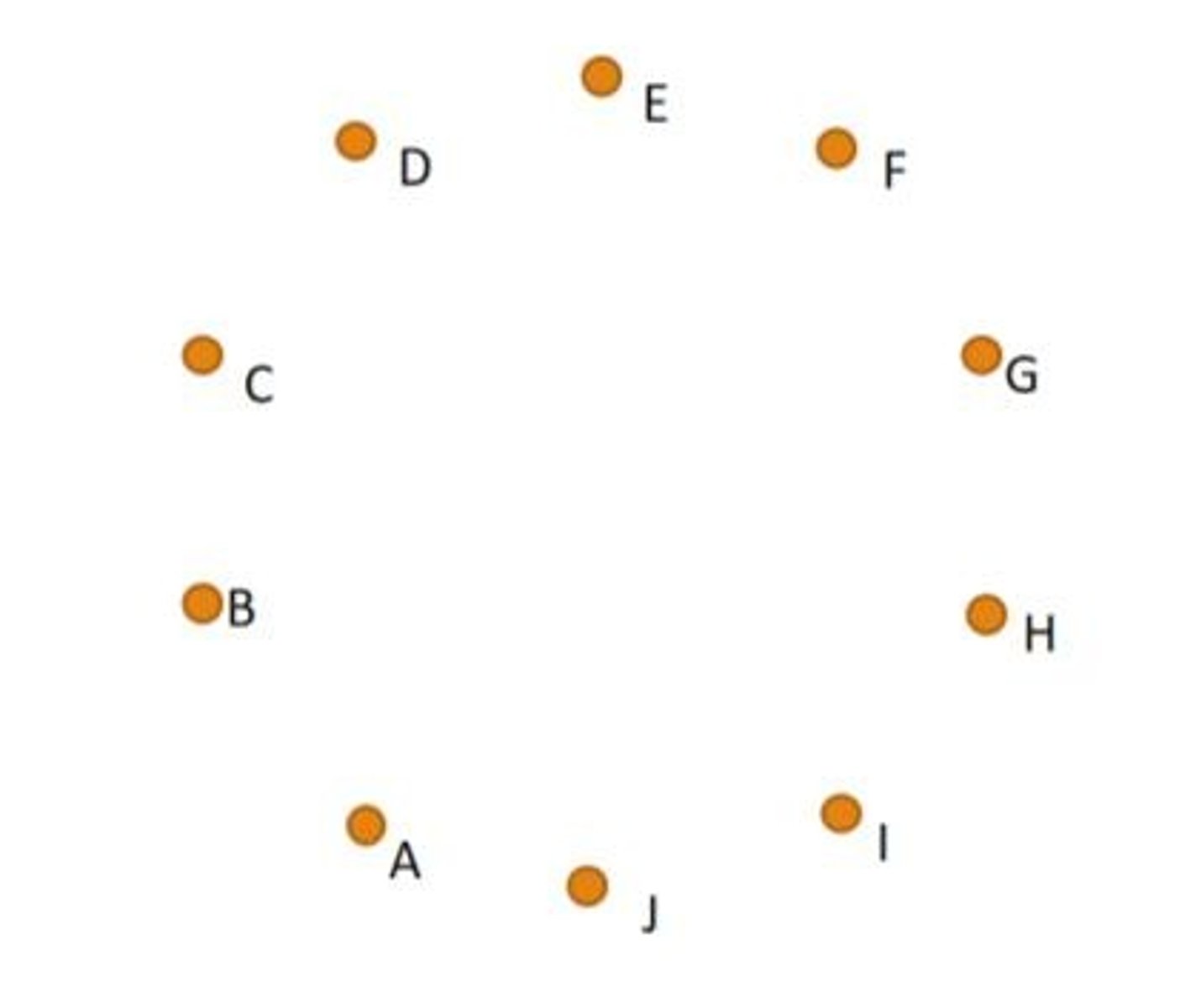
U3: What would be the formula used to solve the handshake problem? Why?

(n(n-1))/2 OR n minus 1 times n over 2

-Divided by 2 to account for double counting

-n(n-1) to represent the number of handshakes each person shakes time the number of people in total

U3: In a star, e+d+a+b+c= ________

180

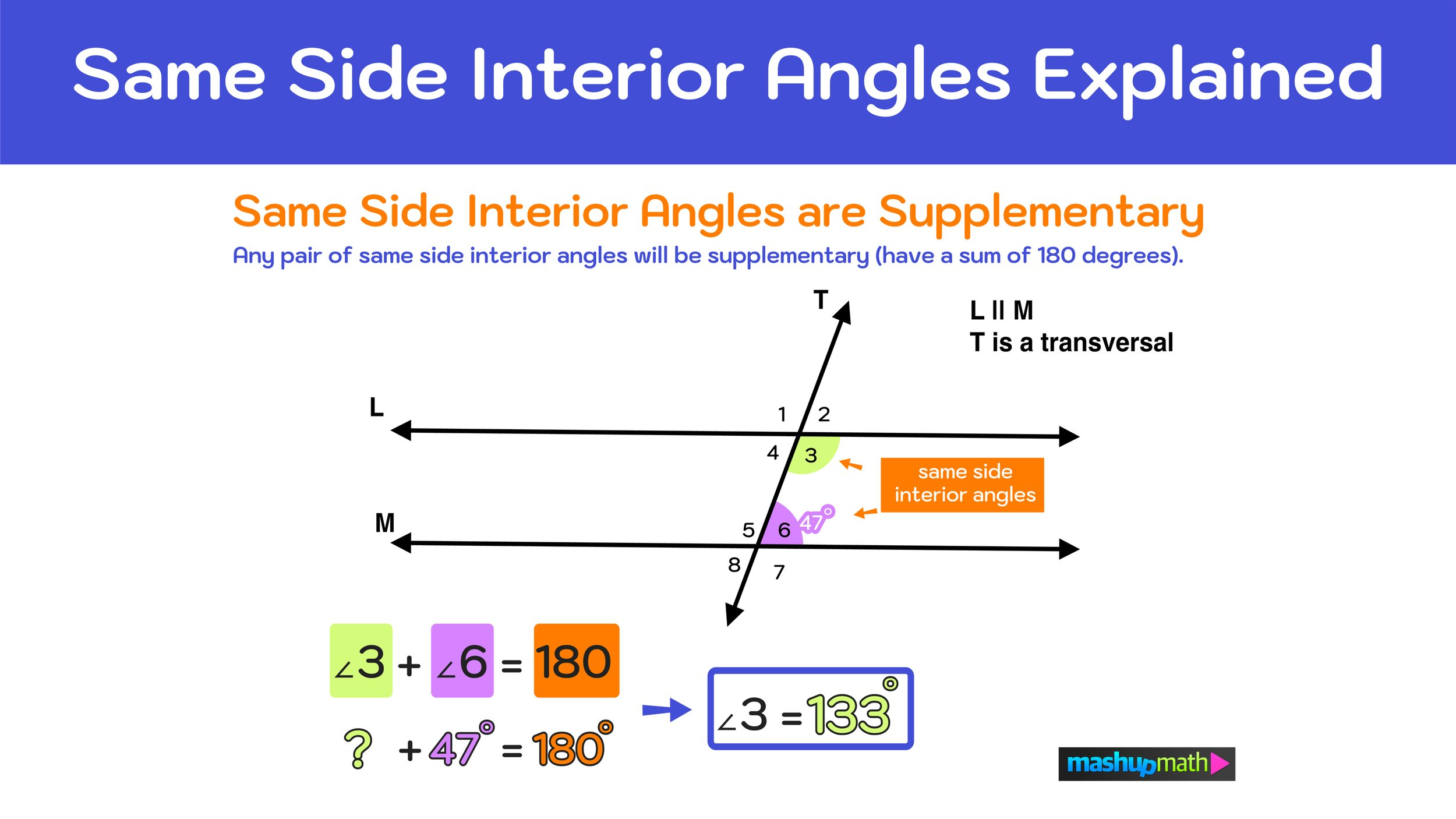
U3:Same side interior angle theorem

If two parallel lines are cut by a transversal, then same-side interior angles are supplementary.

U3: Reflex Angle

an angle that is greater than 180

U3: Define symmetric property, transitive property, and reflexive property

Symmetric= a=b b=c

Transitive = a=b b=c a=c

Reflexive = a=a

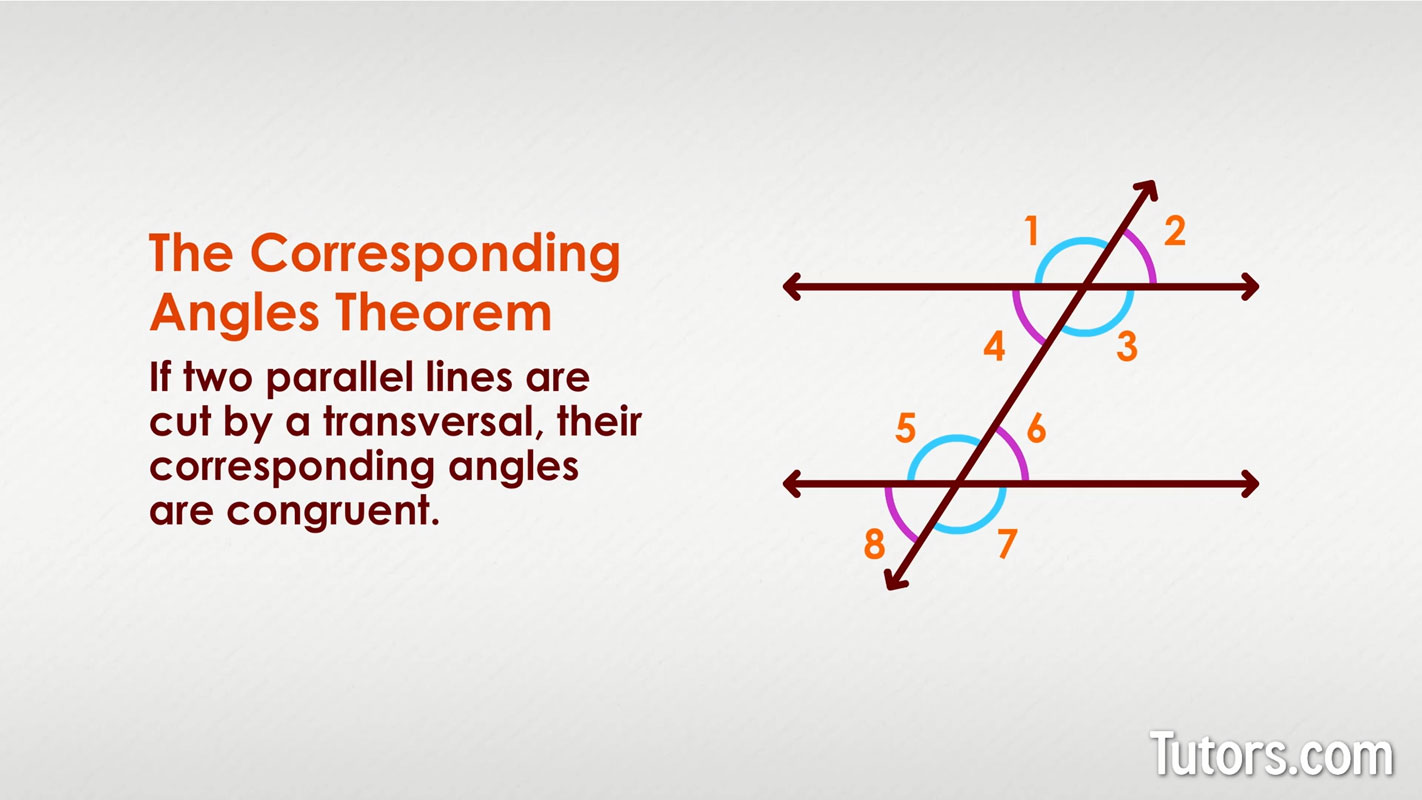
U3: Corresponding Angles Postulate

If a transversal intersects two parallel lines, then corresponding angles are congruent.

U3: Alternate angles theorem

If a transversal intersects two parallel lines, then alternate interior angles are congruent.

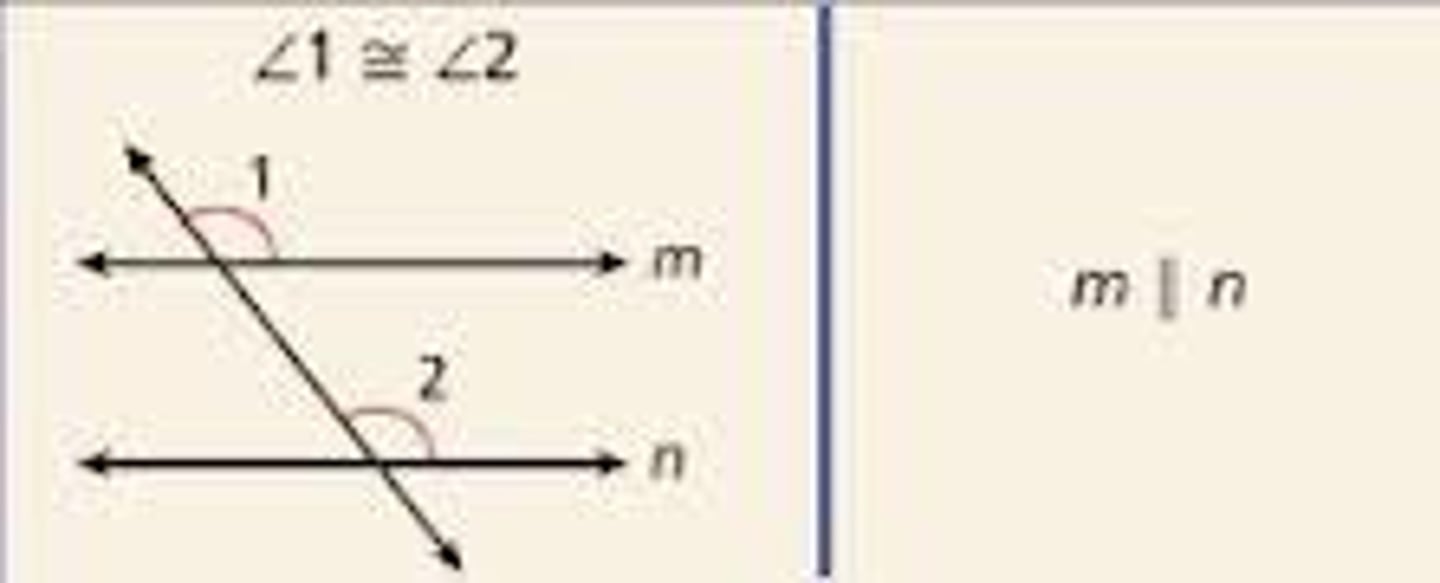
U3: Corresponding angles converse postulate

If two lines are cut by a transversal so that corresponding angles are congruent, then the lines are parallel.

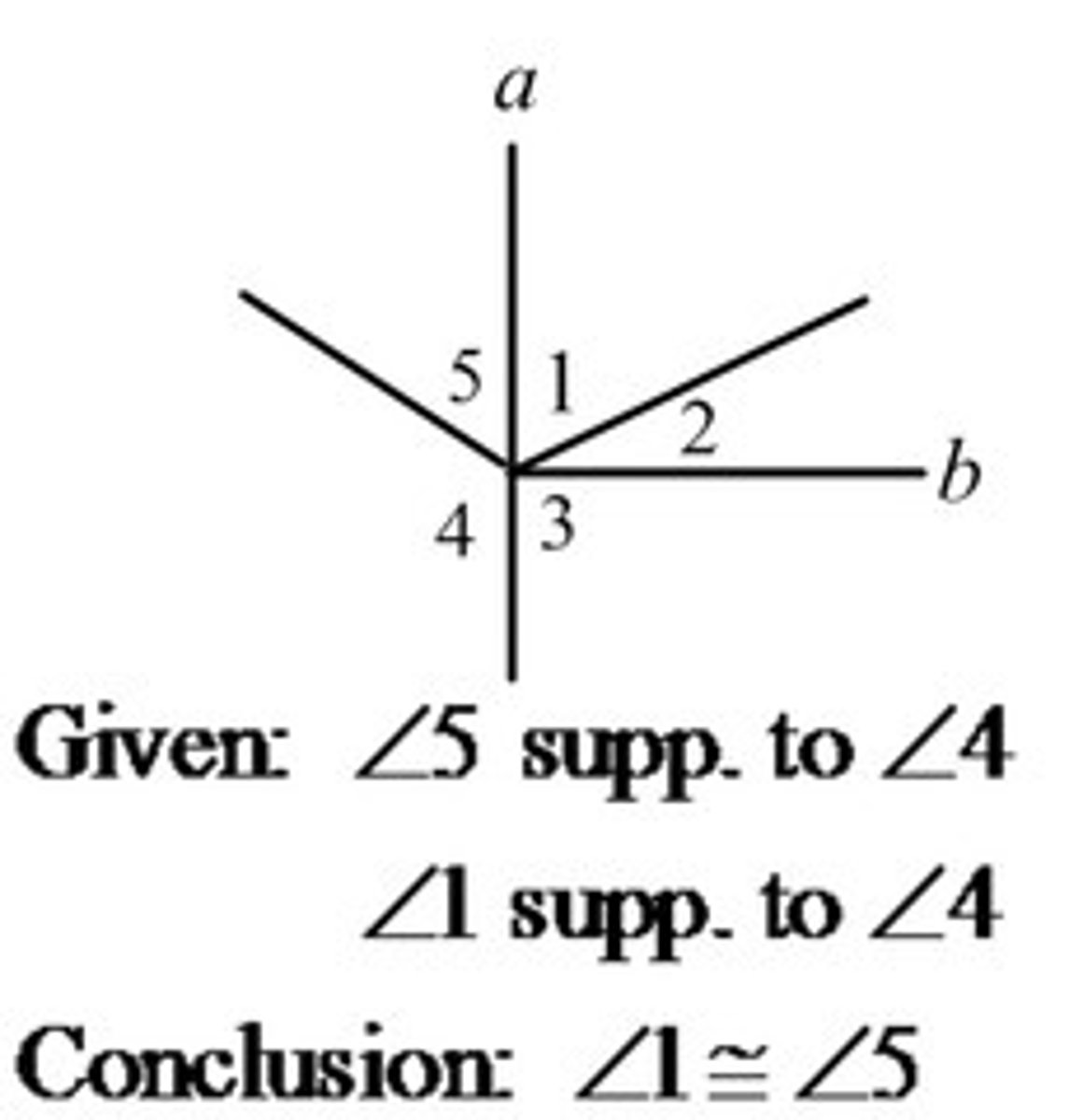
U3:Congruent Supplement Theorem

If two angles are supplementary to the same angle, then they are congruent

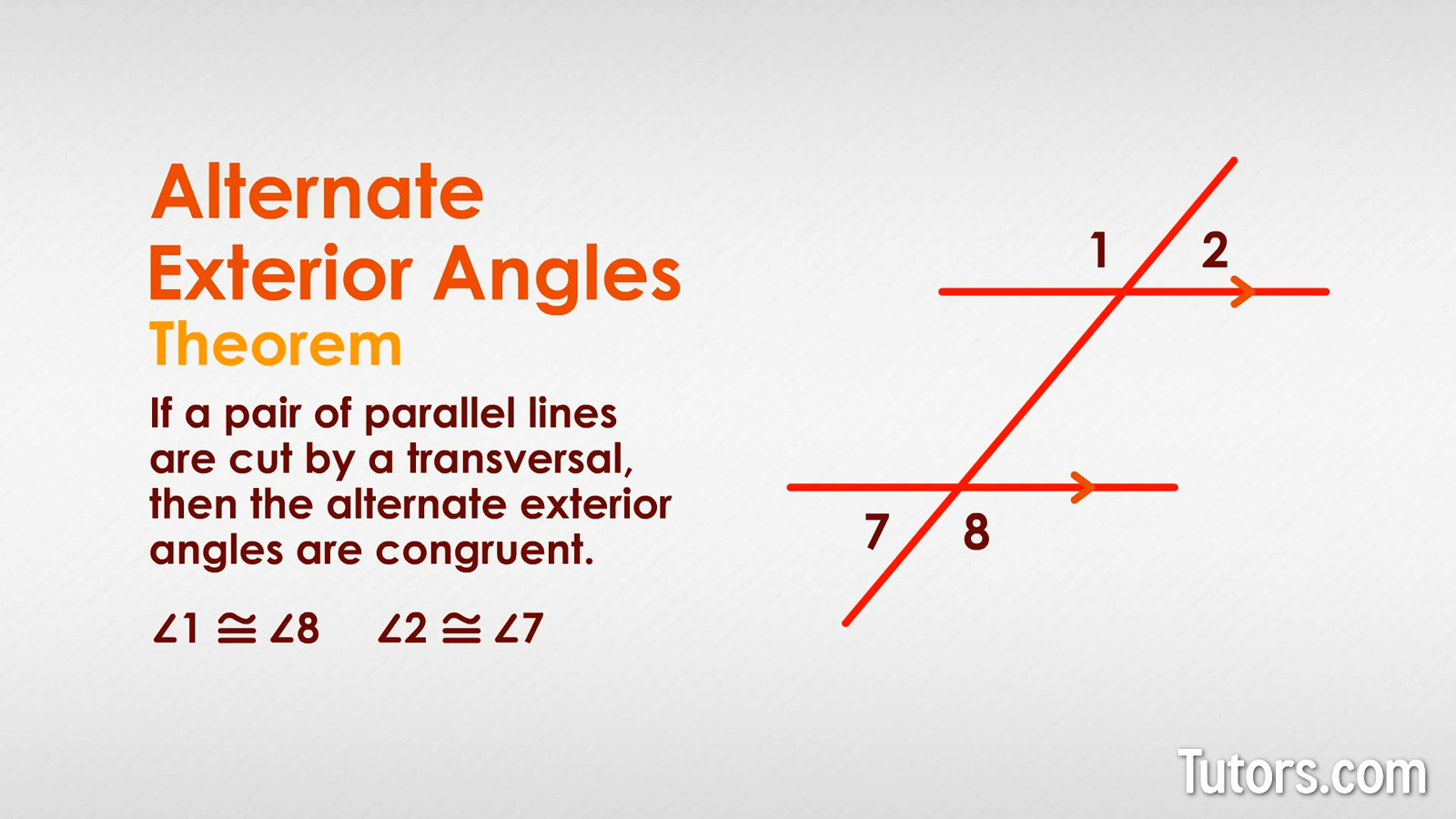
U3: Alternate interior angles converse thorem

If two lines are cut by a transversal so that alternate interior angles are congruent, then the lines are parallel

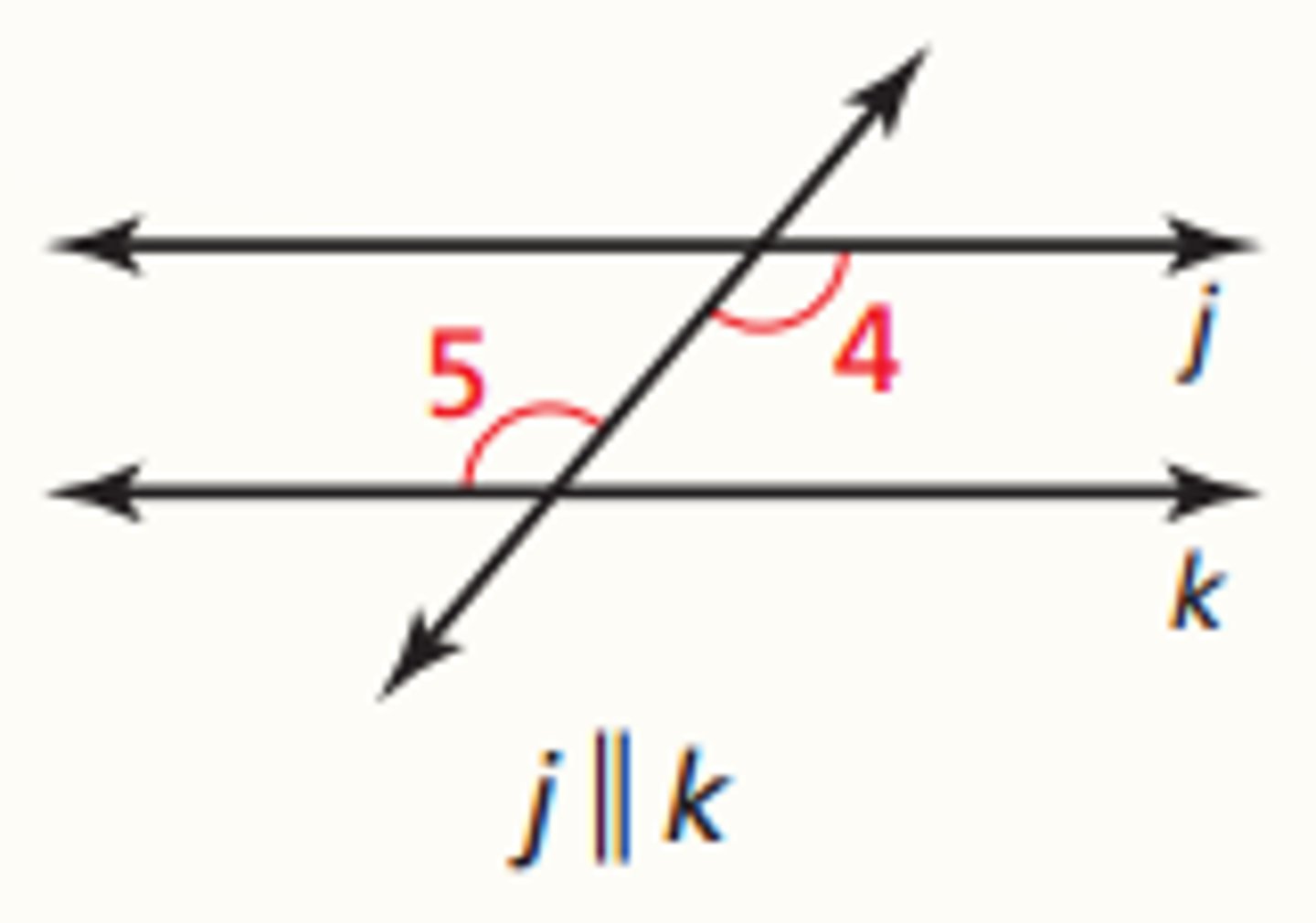
U3:Consecutive interior angles converse theorem

If two lines are cut by a transversal so the consecutive interior angles are supplementary, then the lines are parallel.

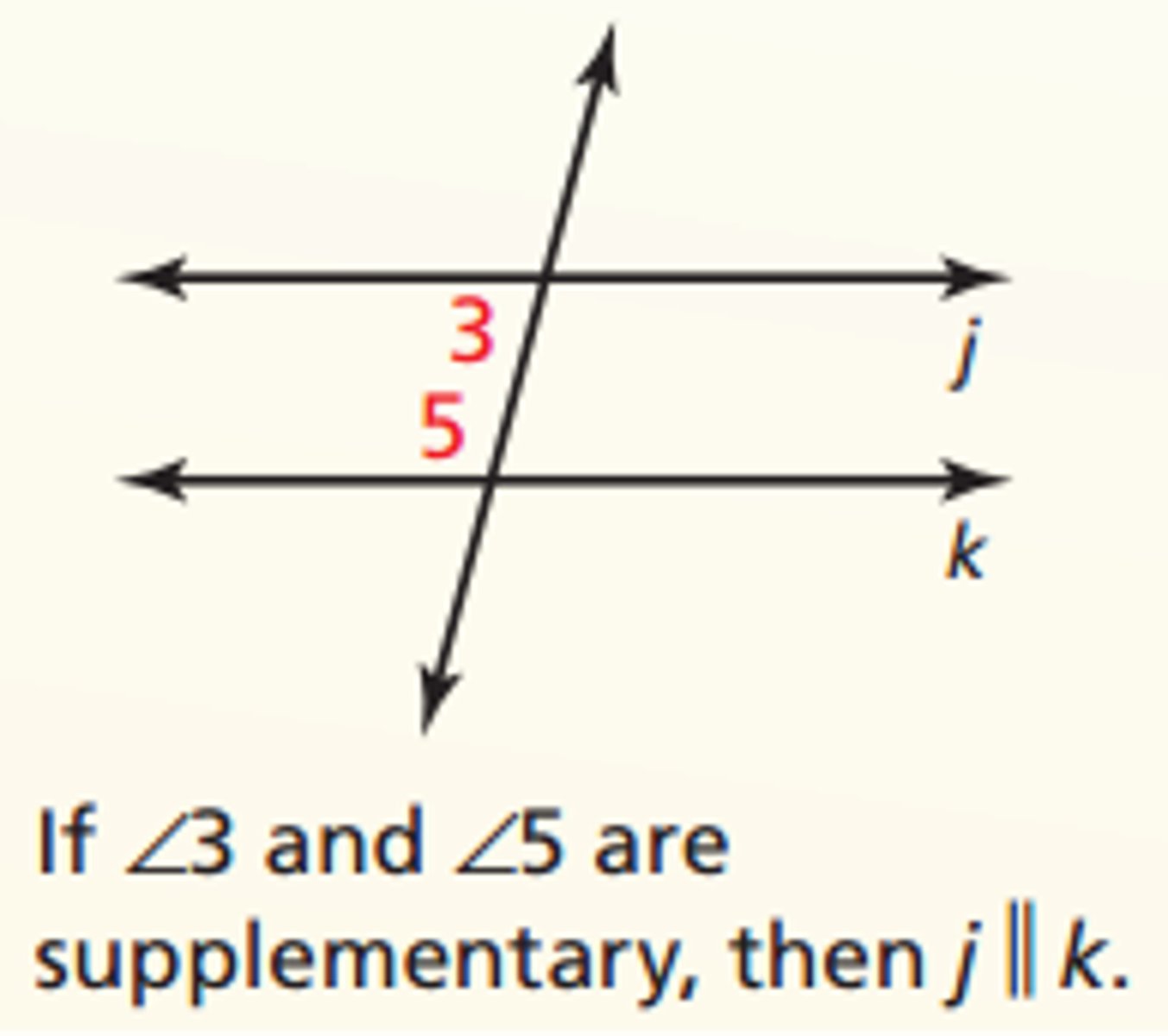
U3: Angle Bisector definition

a ray that divides an angle into two congruent adjacent angles

• EQUIDISTANT from RAYS (not endpoints!!)

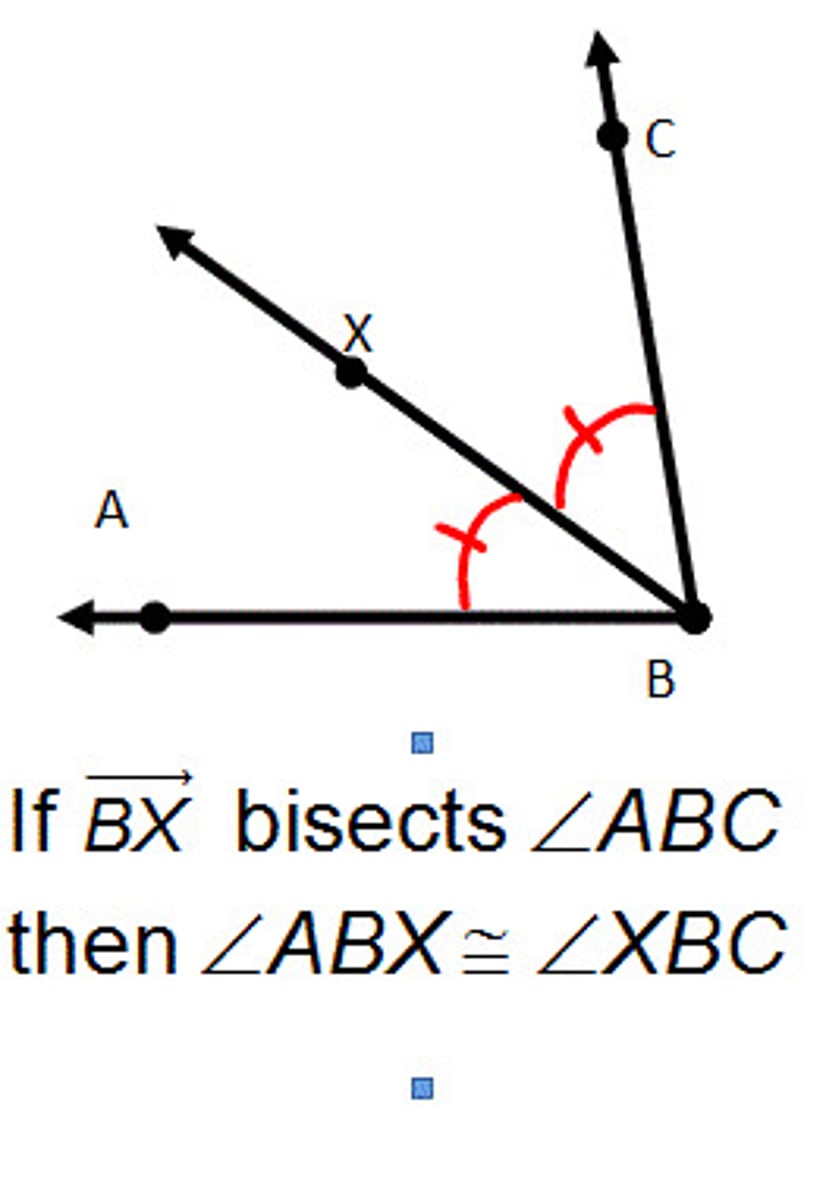
U3: Are corresponding angles always congruent?

NO! Only if the two lines are parallel (corresponding angles postulate)

—> MUST BE stated/marked in the problem/diagram

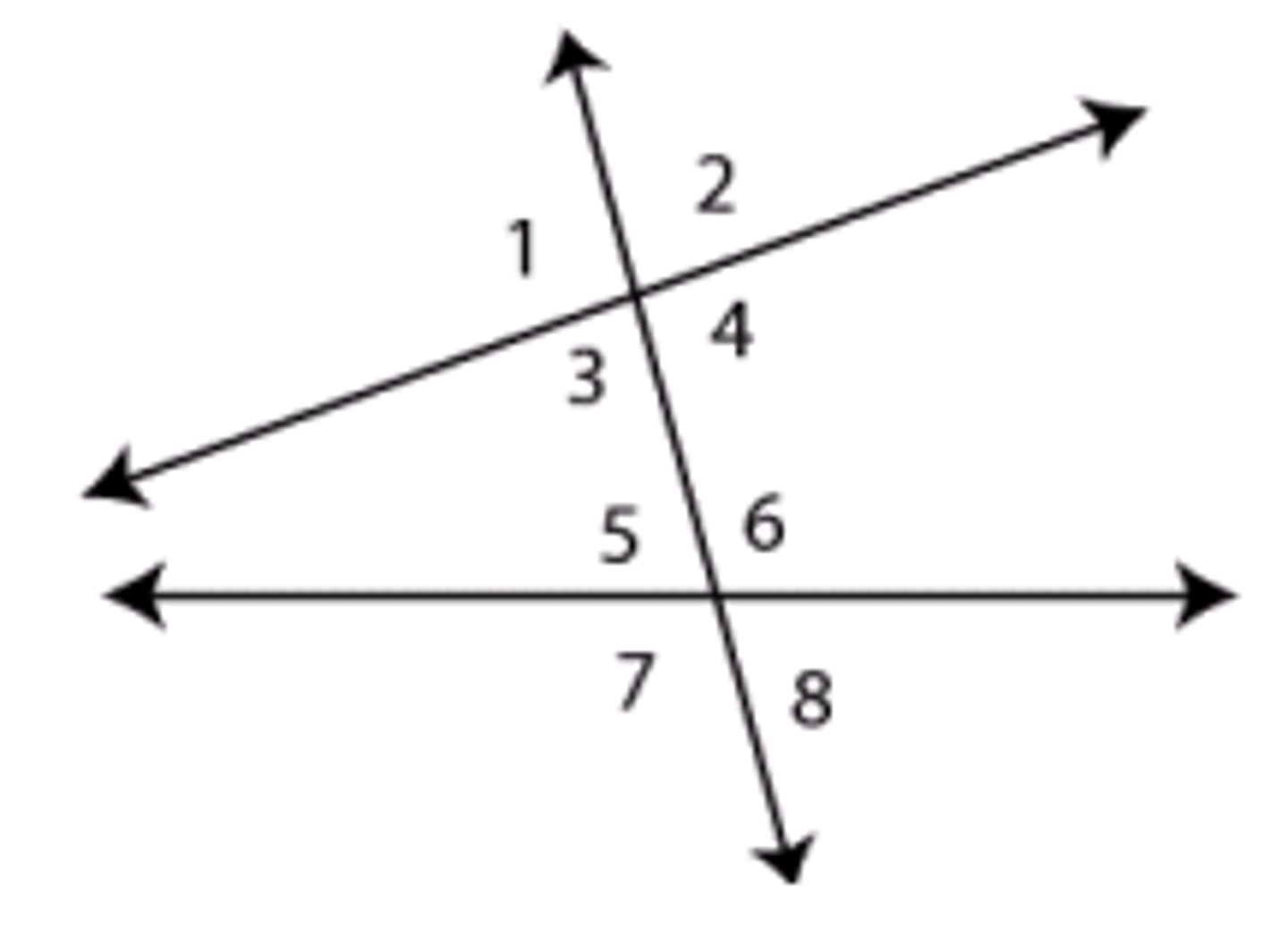
U3:If a transversal intersects 2 parallel lines

_______ angles are ________. ( hint: there are three)

Corresponding angles are congruent

Alternate interior angles are supplementary

Same side interior angles are congruent

REMEMBER: THIS ONLY APPLIES TO PARALLEL LINES LOOK FOR THE ARROWS

U3: What equation do we use to find the number of diagonals in a n sided polygon? How many diagonals per vertex? (Also: what is a diagonal)

(n(n-3))/n

n-3 diagonals per vertex

Diagonal: a straight line segment that connects two non-adjacent vertices (corners) of the polygon

*”n” = reprsents the sides of the polygon

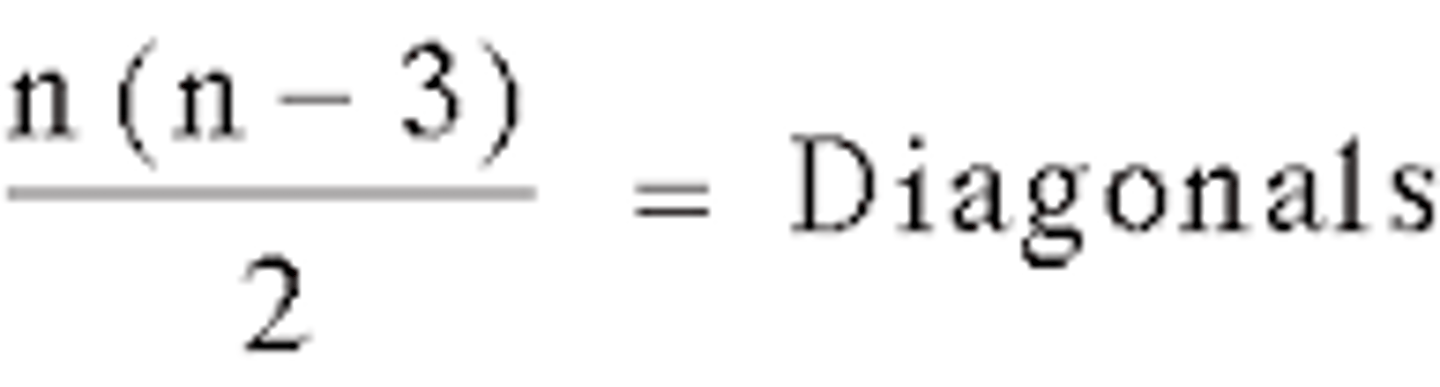
U3:Conditional

If, then

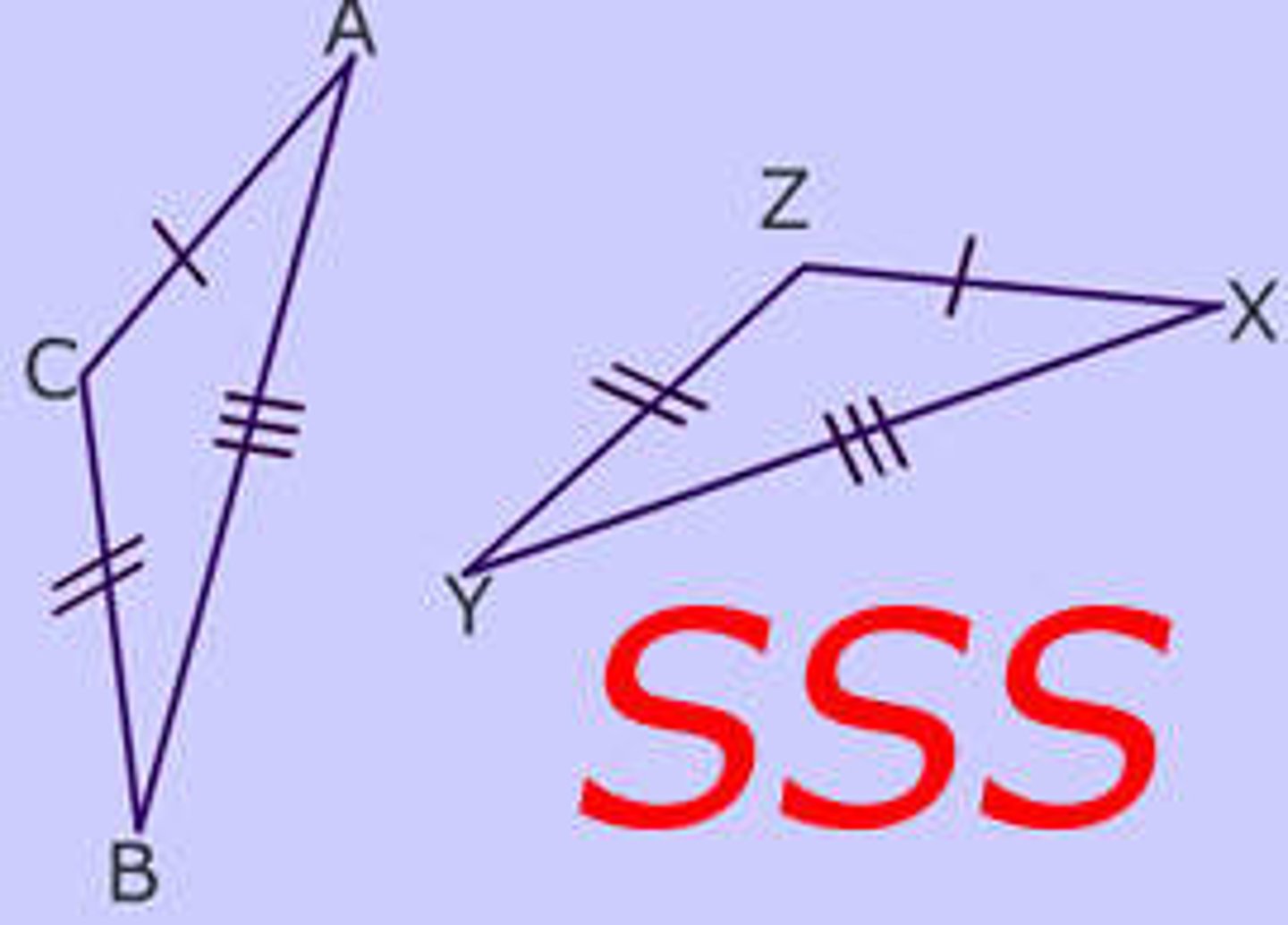
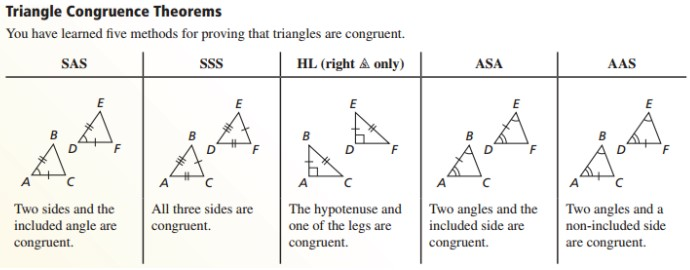
U3:SSS Postulate (Side-Side-Side)

If 3 sides of one triangle are ≅ to 3 sides of another triangle, then the triangles are ≅.

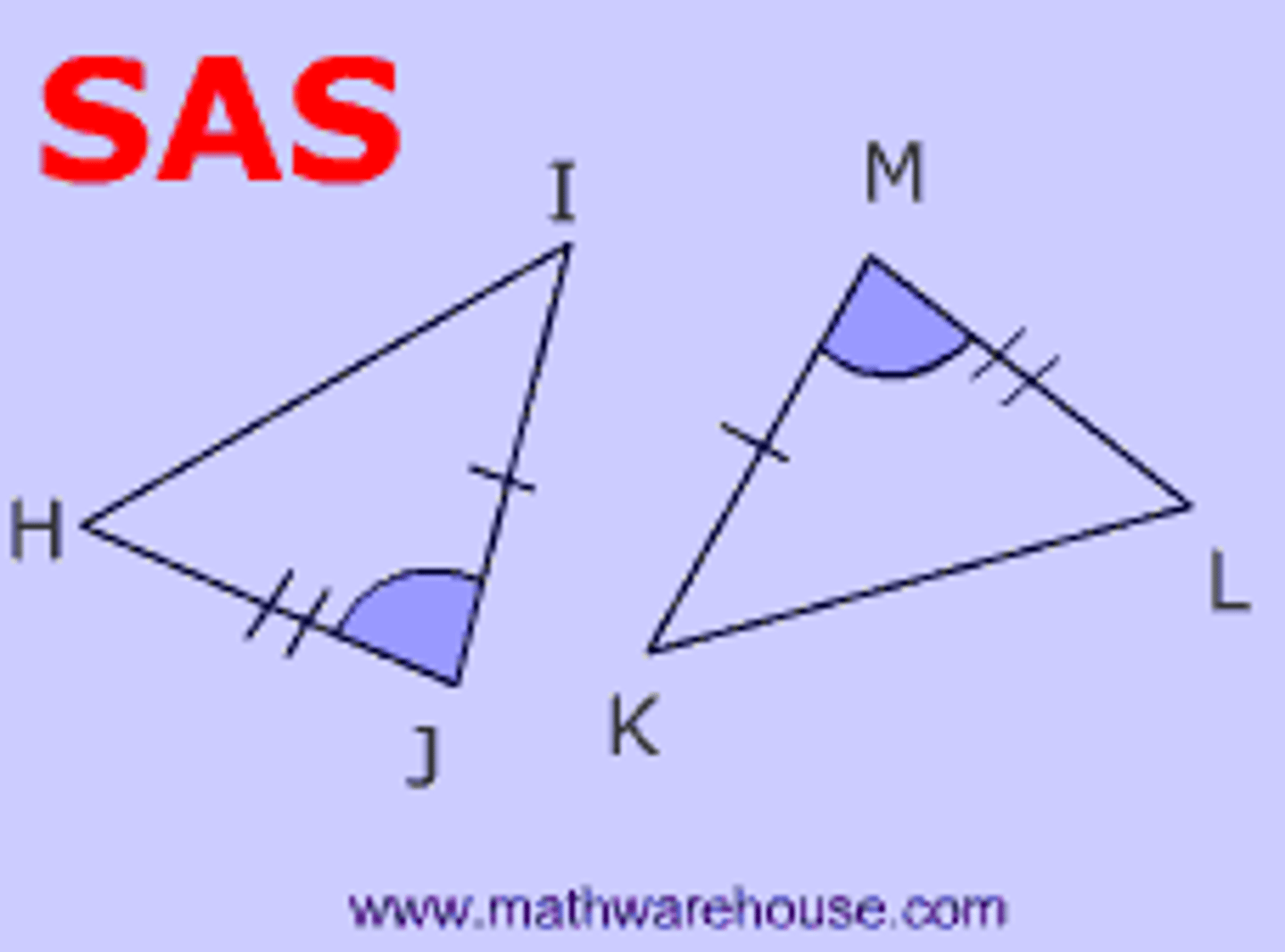
U3: SAS Postulate (Side-Angle-Side)

If 2 sides and the included angle of one triangle are congruent to 2 sides and the included angle of another triangle, then the triangles are congruent

*Included angle: Angle in between

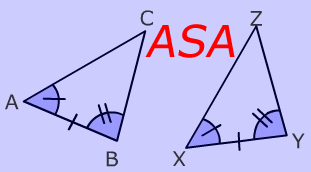
U3: ASA Postulate (Angle-Side-Angle)

If 2 angles and the included side of one triangle are congruent to 2 angles and the included side of another triangle, then the triangles are congruent.

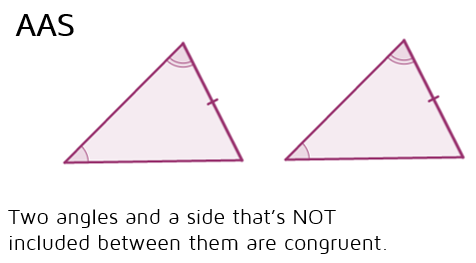
U3: AAS Postulate (Angle-Angle-Side)

If two angles and a side (THAT IS NOT INCLUDED) are congruent to two angles and a side (THAT IS NOT INCLUDED) of another triangle, the triangles are congruent.

U3: HL Postulate (Hypotenuse-Leg)

If the hypotenus and one leg of a right triangle are congruent to the hypotenuse and leg of another right triangle the triangles are congruent.

• MUST prove both triangles are right trinalges before using this

U3: What congruence postulates can you use to prove triangles are congruent?

SAS, SSS, HL, ASA, AAS

NEVER ASS

U3: Does ASS work as a congruence postulate?