1.4.1 data types

integer

• whole number

• negative numbers aren’t integers

• useful for counting things

real

• positive or negative numbers

• can, but do not necessarily, have a fractional part (decimal)

• all integers are real numbers

character

a single symbol used by a computer

string

• a collection of characters

• can be used to store a single character

• useful for storing text a phone numbers which start with 0

boolean

• true or false

• useful for recording data that can only take 2 values

  • state of power button

  • weather a line of code has been executed

representing positive integers in binary

• computers can store whole numbers using binary

• just like humans count in base 10, computers count in base 2, where each step in place represents a value of two times the previous place

• a single binary digit is called a bit

• eight binary digits can be combined to form a byte

• half a byte (four bits) is called a nybble

• the least significant bit of a binary number is the one furthest to the right

• the most significant bit is furthest to the left

8 bit = 128 64 32 16 8 4 2 1

converting from decimal to binary

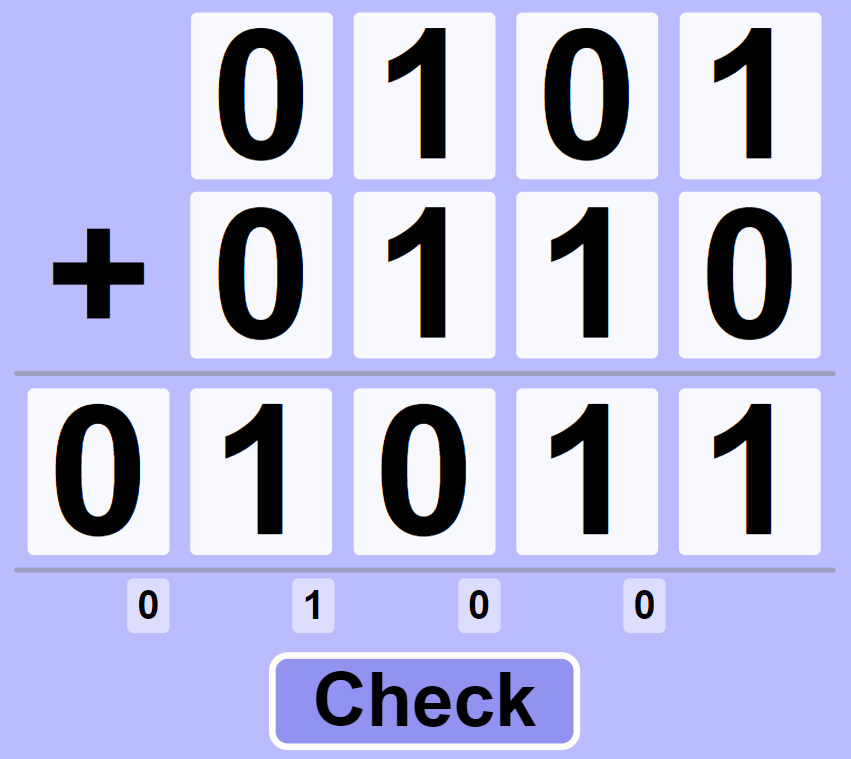
binary addition

0 +​ 0 + 0 = 0 

0 + ​0 + 1 = 1 

0 + ​1 + 1 = 10 

1 + 1 + 1 = 11 

sign magnitude - negative binary

• this is the equivalent of adding a + or - sign in front of a number

• binary can only use 0​ s and 1​ s, so we have to somehow represent + and - using 0​ and 1​

  • leading 1​ is added for a negative number

  • leading 0​ is added for a positive number

• converting from sign magnitude to decimal is as simple as making a note of the most significant bit, remembering the sign and discarding the leading bit

• then convert the remaining bits to decimal using the method explained earlier and add the sign

• for example, the sign magnitude number 101101001​ is negative, because it starts with a 1​

• remove the 1​ and we’re left with 01101001​ which is 105​ in decimal. Add on the minus sign and we have our result: -105​

two’s Complement - negative binary

• two’s complement has the added advantage of making binary arithmetic with negative numbers much more simple

• works by making the most significant bit negative

• for example, with eight bits (a byte) the most significant bit, usually 128, represents -128

• converting to two’s complement is as simple as flipping all of the bits in the positive version of a binary number and adding one

• for example, the binary byte representing 7 is 00000111​

• flip all the bits and you get 11111000​ , adding one gives us 11111001

subtracting in binary using two’s complement

• in five bit two’s complement, 8 is 01000​ and -12 is 10100​

  • -16 +4 = -12

• five is the minimum number of bits required in order to represent -12​

• the two’s complement numbers are then added using the same technique for adding that was explained earlier before the result can be read off as 11100​

• checking the result, -16 + 8 + 4 = -4​ so the calculation is correct

hexadecimal

base 16

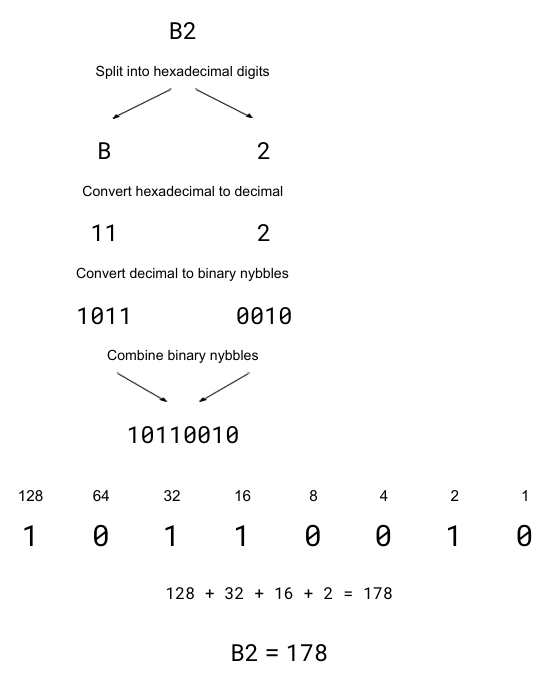
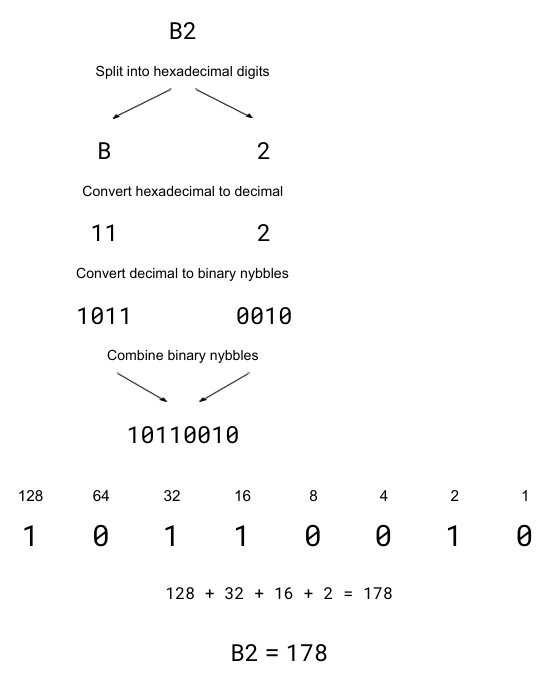
converting from hexadecimal to binary

• first convert each hexadecimal digit to a decimal digit and then to a binary nybble before combining the nybbles to form a single binary number

• split into hexadecimal digits

• convert hexadecimal to decimal

• convert decimal to binary nybbles

• combine binary nybbles

converting from hexadecimal to decimal

convert to binary and then convert from binary to decimal

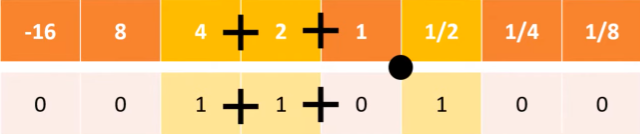
fixed point binary

• position of the point is fixed on the number line

• the range of numbers we are able to store is limited as some positions on the number line are being used to store the fractional part of the number

  • the largest number we can store with 8 bits is 15.875 = 01111 1111

• binary point is places between 1 and ½

  • 6.5 = 0011 0100

  • 4 + 2 + ½ = 6.5

• if the number is negative, the most significant bit (MSB) must be a 1 as it is negative

  • -6.5 = 1100 1100

  • -16 + 8 + 1 + ½ = -6.5

mantissa and exponent

• mantissa = the number itself

• exponent = the position of the binary point in the number

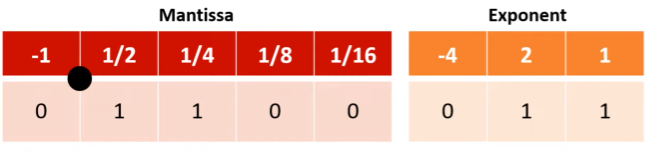
floating point numbers in binary

• binary point always starts after the MSB, between the first two digits in the mantissa

• this is then ajusted by the exponent

• we convert the exponent (MSB of exponent is negative)

• id our exponent is +3, we move the binary point in our mantissa 3 places to the right

  • move left is number is a negative

• add up columns that have a 1 in them

normalisation - floating point binary

• floating point numbers are normalised to make sure that they are as precise as possible in a given number of bits

• essentially equates to making as much use of the mantissa as possible

• to normalise a binary number, adjust it so that it starts 01​ for a positive number of 10​ for a negative number

  • normalise the binary number 000110100101​ which is a floating point number with an eight bit mantissa and a four bit exponent

• split the number into mantissa and exponent

• 00011010  0101 = mantissa, exponent

• adjust the mantissa so that it starts 01​ or 10

• positive number, so we will move all of the bits two places to the left and add zeros to the end of the mantissa

• new mantissa is 01101000​

• because we’ve made the mantissa bigger by shifting the bits two positions to the left, we must reduce the exponent by two so as to ensure the same number is still represented

• the current exponent is 5₁₀ so, subtracting two, the new exponent must be 3₁₀ which is 0011​₂ in binary

• 01101000 0011 = mantissa, exponent

• we now have a mantissa that starts with the digits 01​

• a positive normalised number

addition of floating point numbers

1. work out where the binary point should be in each number using the exponent

2. line both numbers up on the normal binary line so the binary points are in the same position

3. add the numbers up in the normal way following the rules of binary addition

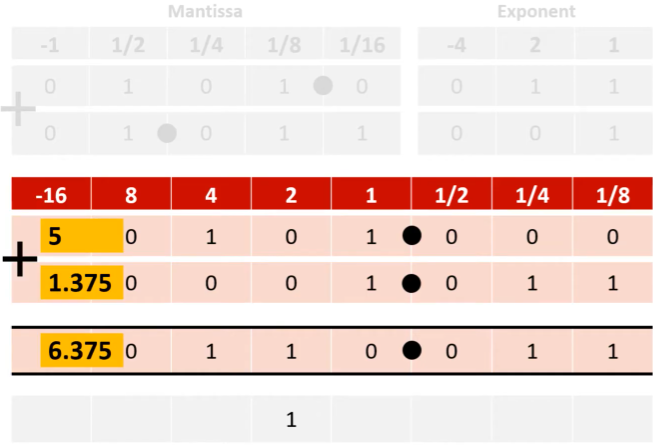
subtraction of floating point numbers

• work out where the binary point should be in each number using the exponent

• align both numbers on the binary line, ensuring the binary points are in the same position

• subtract the numbers in the regular manner, applying binary subtraction rules

  • start on right with the least significant bit

  • copy each bit as it appears up to and including the first 1

  • swap all remaining bits (0s become 1s, and 1s become 0s)

  • then add the numbers

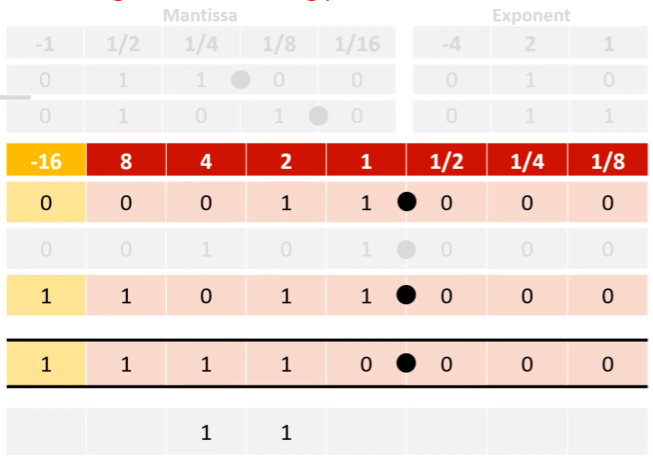
storing floating point arithmetic results back as a normalised floating point number

• move binary point so it sits between the first 0 and 1

  • 3 places for example

• so to get it back in the correct position it must be moved 3 places right meaning the exponent is 3

• store the mantissa (number from the original number line)

• if there is not enough space in the mantissa to represent the entire number

  • increase total number of bits we can use to store the normalised floating point number

bitwise manipulation - shifts

• a shift performed on binary numbers is called a logical shift

• two varieties

  • logical shift left

  • logical shift right

• a shift involves moving all of the bits in a binary number a specified number of places to the right or to the left

• this can be thought of as adding a number of leading or trailing zeros

• example

  • perform a logical shift left by three places to the binary 10010110

  • logical shift left by three places is the same as adding three trailing zeros

  • result is therefore 10010110000

  • the result of a logical shift is a multiplication (or division if shifting right) by two to the power of the number of places shifted

  • the example has the effect of multiplying the original number by 2₃ = 8

  • a logical shift left by one place has the effect of doubling the initial number

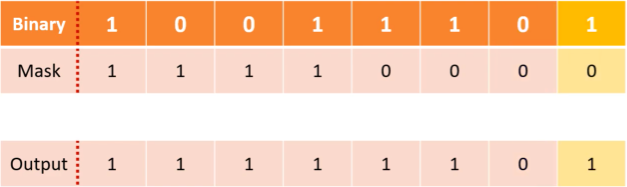
bitwise manipulation - masks

• used to isolate and extract or modify specific bits in a binary number

• by performing a bitwise AND, OR, or XOR operation with a mask, certain bits can be turned on or off without affecting others

• OR shown in picture

ASCII

• American Standard Code for Information Interchange

• uses 7 bits to represent 2⁷ = 128 different characters

• the capital letters A-Z are represented by codes 65-90 while the lower case letters a-z correspond to codes 97-122

• there are also codes for numbers and symbols

• while 128 characters is plenty for standard letters, numbers and symbols, ASCII soon came into trouble when computers needed to represent other languages with different characters

unicode

• solves the problem of ASCII’s limited character set

• uses a varying number of bits allowing for over 1 million different characters

• enough capacity to represent a wealth of different languages, symbols, and emoji

binary, denary, hexadecimal

• binary = base-2 numeral system using only 0 and 1 digits

• denary = base-10 system using digits 0-9

• hexadecimal = base-16 system using digits 0-9 and letters A-F