Physics - Wave interactions and Standing waves (Harmonics)

Superposition

When two or more longitudinal or transverse waves meet, the resulting displacement at each point will be the vector sum of the displacements of the component waves.

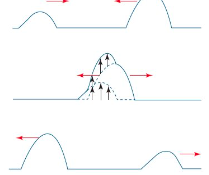
Constructive interference

Occurs when two waves combine to give a greater resultant displacement. When waves are in phase, it will be a maximum.

Complete constructive interference occurs when two waves of the same amplitude that are in phase combine to give a wave of double the amplitude.

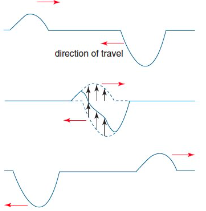
Destructive interference

Occurs when two waves combine to give a smaller resultant displacement (reduction in amplitude). This effect is a maximum for similar waves 180 degrees out of phase.

Complete destructive interference occurs when two waves of equal amplitude (exactly 180 out of phase) produces zero displacement.

Resonance and its special effects

Occurs when the frequency of a forcing vibration equals the natural and resonant frequency of an object. The vibrations from one object cause a strong vibration in another. If the amplitude of the vibrations becomes too great, the object can be destroyed. Special effects occur with resonance:

• The amplitude of vibration increases

• The maximum possible energy from the source is transferred to the resonating object

Antinodal and Nodal line

• Antinodal line: maximum reinforcement - compression with compression = constructive interference

  • Equal distance between speakers parallel.

• Nodal line: total annulment - compression with rarefraction = deconstructive interference.

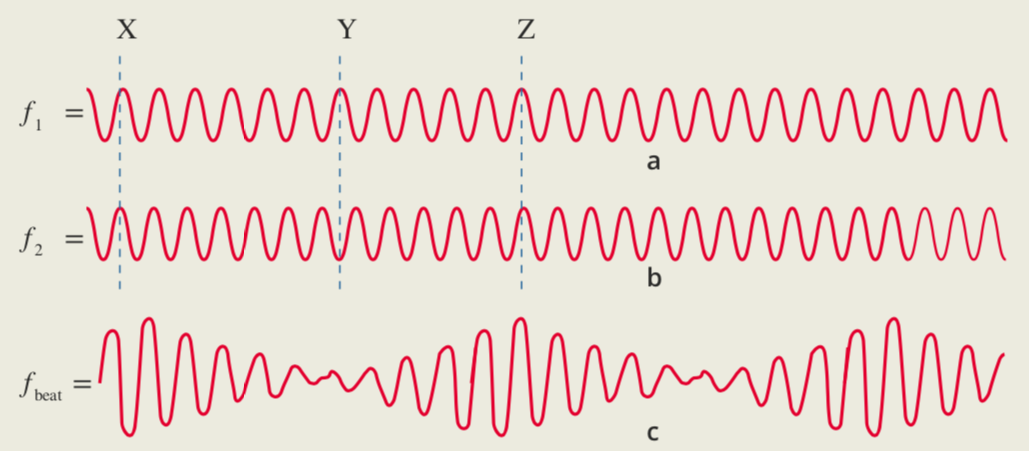
Beats

If two sound waves of equal amplitude but slightly different frequency are combined, the resulting sound has a regular pulsation (beat)

The frequency of the beat is simply the difference between the frequencies of the sounds that are superimposed.

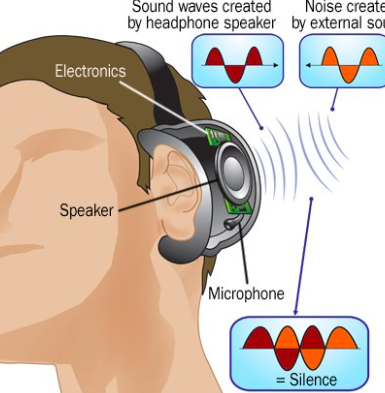
Noise cancellation (headphones)

Headphones records the outside unwanted noise and produce a wave that exactly is opposite in phase (if there is maximum amplitude, there will be a minimum in the amplitude produced by the headphones). This is an example of destructive interference.

Free oscillations (free vibration)

An object given a single impulse, oscillates at its natural frequency

Forced oscillations (resonance)

Impulses introduced in time with natural frequency of an objects oscillation.

Resonance - Swing analogy

• A swing is pushed once and oscillates at its natural frequency. This is entirely dependent on the design, materials length of rope etc.

• It is possible to push the swing at the right time so that you match its natural oscillation

• Additional energy you add will increase the amplitude rather than work against it. Overtime, the swing will go higher and higher (resonance).

• The frequency with which you push is the forcing frequency - anything that does not match the natural frequency will end up fighting the swing.

Conclusion: Amplitude of oscillations within the resonating object will increase dramatically. The maximum possible energy from the source creating the force vibration is transferred to the resonating object.

Resonance - PROS and CONS

• PROS: musical instruments and loudspeakers - the sounding boards of pianos and the enclosures of loudspeakers are designed to enhance and amplify particular frequencies.

• CONS: Undesirable in mechanical systems such as car exhaust systems, can also cause ropes and screws to loosen.

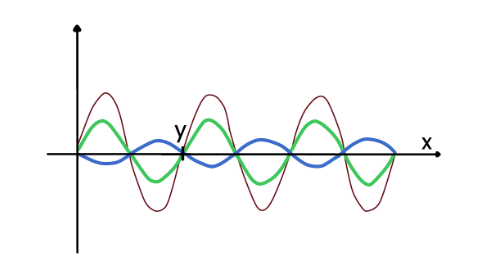
Standing waves

Occur when two waves of the same amplitude and frequency are travelling in opposite directions through a medium.

Waves meeting barriers

• A wave reflecting from the fixed end of a string will undergo a phase reversal; that is, a phase shift of λ/2

• A wave reflecting from the free end of a string will not undergo a phase reversal

Why

Why do standing waves do not appear to ‘move’?

Occurs due to the constructive and destructive interference between incident and reflected waves of the same wavelength and amplitude.

Frequency of the wave needs to match a natural resonant frequency of string or air column.

String vibration

Stretched strings will freely vibrate at a particular natural frequency, known as its fundamental frequency. This frequency depends upon the length of the string, mass per unit length and tension.