Class 2 - Sampling Distribution and Central Limit Theorem

Define: Statistical Inference

Statistical inference is reaching a conclusion about a population parameter based on information from a sample.

What are the two approaches to statistical inference?

• Estimating Parameters

• Testing Hypotheses

Describe: Estimating Parameters

Basic statistical inference

Two types

• Point estimates: a single numerical value from a sample (e.g. sample mean) and is a “best approximation” for its corresponding population parameter (e.g. population mean)

• Interval estimates: a range of values calculated from the sample and is “likely to include” the population parameter of interest (e.g. confidence intervals)

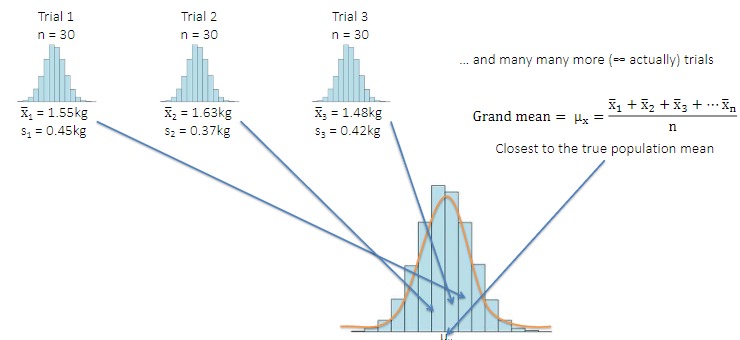
Define: The Sampling Distribution of the Mean

The mean of a representative sample is usually a good estimate for the population mean, but the mean of a sampling distribution is a better estimate of the population mean.

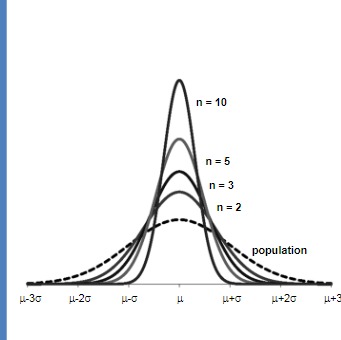
Describe: The Standard Error of the Mean

• Another way of saying “the standard deviation of the sampling distribution”, estimates the spread of a sampling distribution

• Measures how much the sample statistic varies from sample to sample

• Function of sample size, the larger the sample, the smaller the standard error

• S.E = σ/(sqrt: n)

Define: The Central Limit Theorem (CLT)

Given a population of any functional form (normally or non-normally distributed) with a mean μ and a standard deviation σ

The sampling distribution of sample means computed from samples of size n from the population will have mean μ and a standard deviation σ/(sqrt: n) and will be approximately normally distributed if n is sufficiently large

Can CLT be applied to skewed data?

Yes, if a sufficiently large number of samples are taken, even from skewed data, we can retrieve approximately normal distributions.