Chapter 5 Materials

stiffness

strength is understood to be critical, but this is often taken for granted — the resistance to elastic deformation

tension, compression, bending, and torsion

real loading situations can be decomposed into common modes of …

elastic extension or compression

σ=F/A

ε=σ/E

ε=δ/L₀

Relation between load and extension: δ=FL₀/AE

Stiffness: S=F/δ = AE/L₀

Shape of the cross section does not matter

uniform stress when loaded in tension with force F

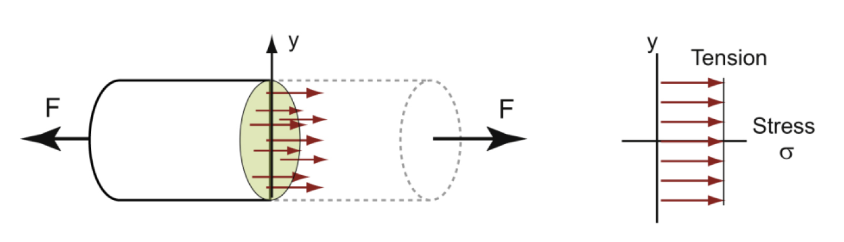
elastic bending of beams

bent into a curve; stress is highest at the top of the surface (stretched) and the lower surface is compressed

beam of rectangular cross-section loaded in bending with moment M₁ giving radius of curvature R.

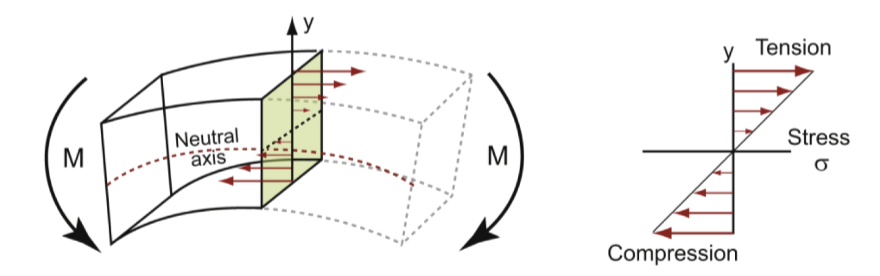
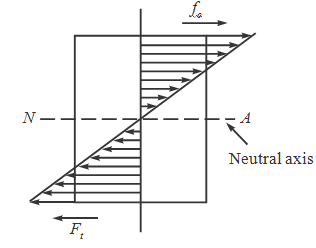
linearly

stress of elastic bending of a beam varies ________ from tension to compression, changing sign at the neutral axis

design process

1. Translation

2. Screening, based on constraints

3. Ranking, based on objectives

4. Documentation, to give greater depth

minimizing weight of a light, stiff tie-rod

• constraints: length, L₀, maximum extension under load δ, stiffness of S=F/δ, reasonable toughness

• objective: minimize mass

• free variables: material, cross-sectional area

• objective function: m=AL₀ρ

S=AE/L₀

• eliminate free variable area A: m=SL₀²(ρ/E)

• S and L₀ are specified; the lightest tie-rod uses a material with the smallest ρ/E.

• Invert to consider maximum values, yielding material index: M_t = E/ρ (specific stiffness).

reasonable toughness

should allow if necessary some plastic deformation before fracturing; ie not brittle (material should not just catastrophically fail)

Objective function

equation describing the quantity to be maximized or minimized

specific stiffness

E/ρ; adjust elastic modulus by density

minimizing material cost

• For material price C_m [$/kg], the cost of material for a component of mass m is just mC_m

• Objective function for material cost of tie, panel, or beam → C=mC_m = ALρC_m

• Leads to indices as before, replacing ρ with ρC_m

  • Example: M_t=E/(ρC_m) for a tie-rod

Minimizing embodied energy in materials production

• For embodied energy E_m, [J/kg], put into materials during materials production from the ore or feedstock.

• Objective function for the materials cost for a tie → E_e = mE_m = ALρE_m

• Leads to indices as before, replacing ρ with ρE_m.

  • For example, M_t = E/(ρE_m) for a tie-rod

screening

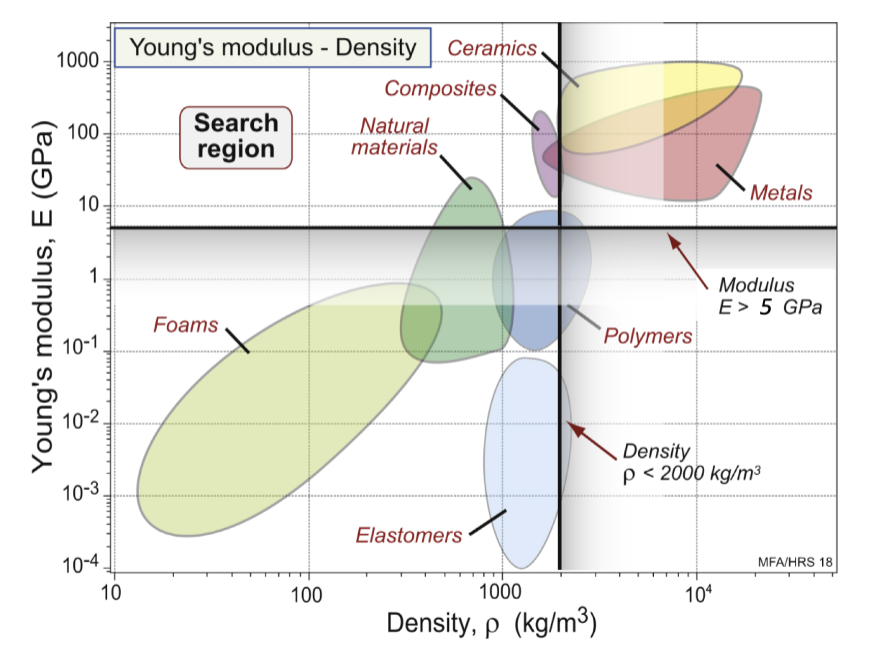
attribute limits on charts; these constraints can be plotted as horizontal or vertical lines; for example, on the E-ρ chart: E > 5 GPa, density < 2000 kg/m³

simple constraints eliminate materials that don’t meet guidelines

ranking

indices on charts - selection guidelines

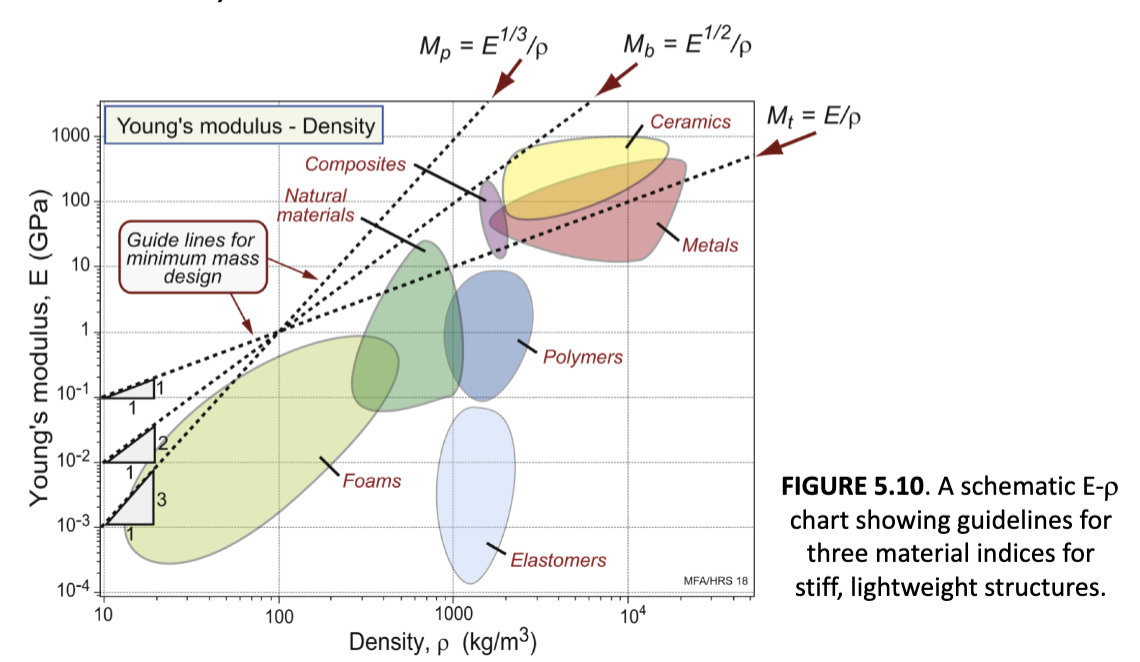
consider the design of light, stiff components using the E-ρ chart. Consider M=E/ρ = c (a constant)

take logs: logE - logρ = logc

rearrange: logE = logρ + logc → form of straight line

slope of lines on log-log charts: tie

M=E/ρ = c

logE - logρ = logc

logE = logρ + logc

Slope of 1

slope of lines on log-log charts: beam

M=E^½/ρ = c

½logE - logρ = logc

logE = 2logρ + 2logc

Slope of 2

slope of lines on log-log charts: panel

M=E^1/3/ρ = c

1/3 logE - logρ = logc

logE = 3logρ + 3logc

Slope of 3

equally well; above; below

All materials on a line perform _________; those ______ are better, and those _______ are worse

direction that gives better material index to eliminate materials

move the line in the …; family of parallel lines, each one at a particular value of the material index of interest, M. best materials are above the line furthest perpendicularly

one tenth

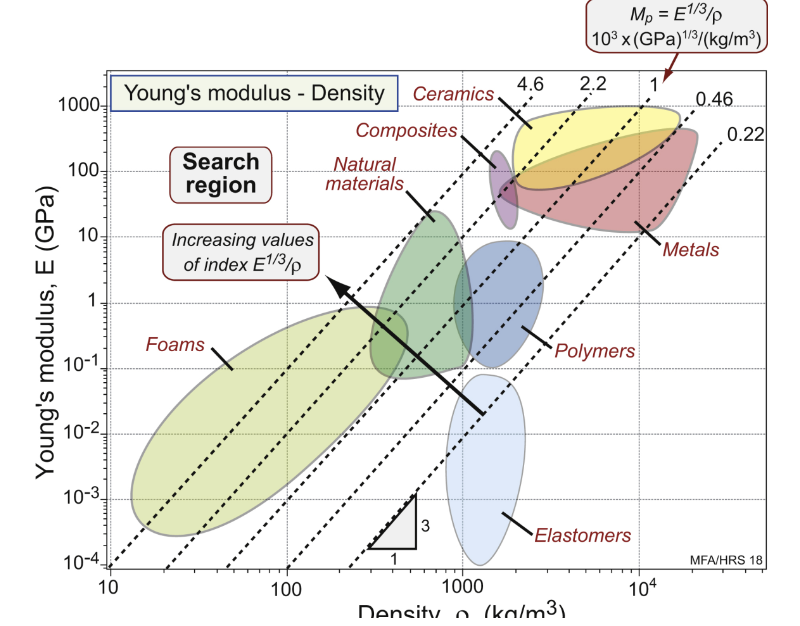
example of comparing material indices: material with M = 2.2 is ________ the weight of the material with M = 0.22

light levers for corkscrews

light stiff beam; constraints: length L, rectangular cross-section, maximum deflection δ, stiffness S, impact-resistant

Objective: minimize mass

free variables: material, area of cross-section

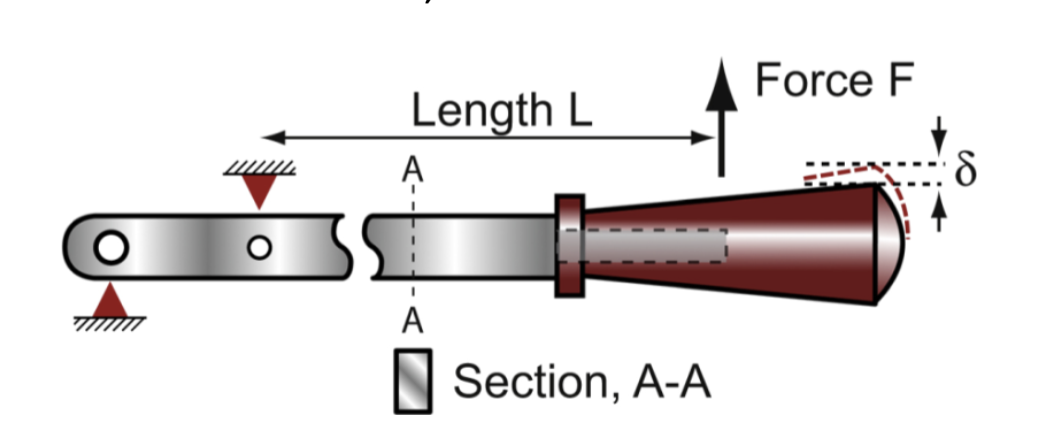
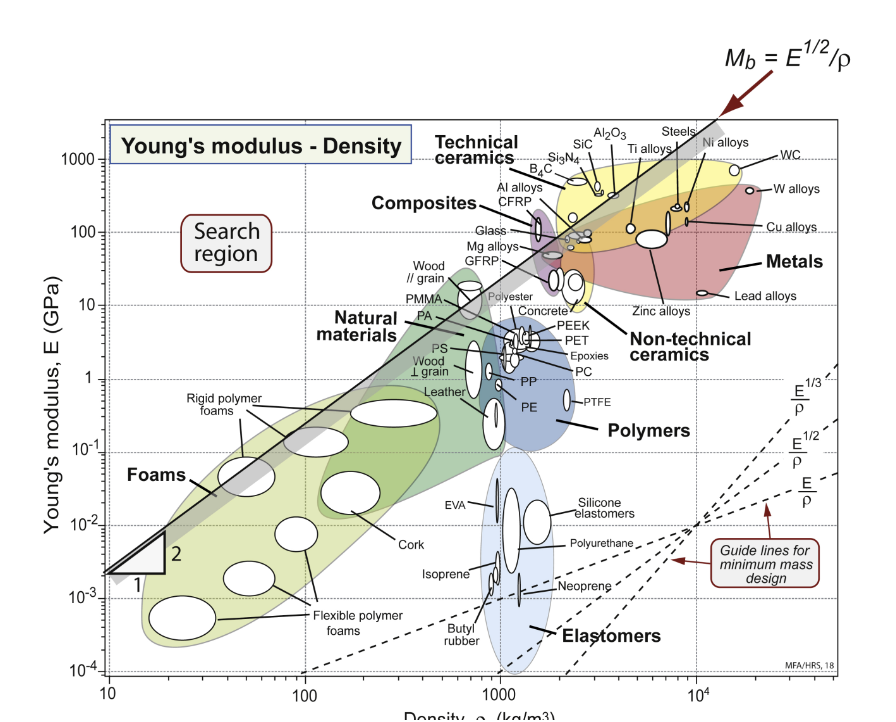
limit possibilties

selection line positioned to ________________, some of which are too brittle

Al2O3, SiC, Si3N4, B4C, CFRP, wood || grain, rigid polymer foam

list the seven materials with the best M_b in the chart

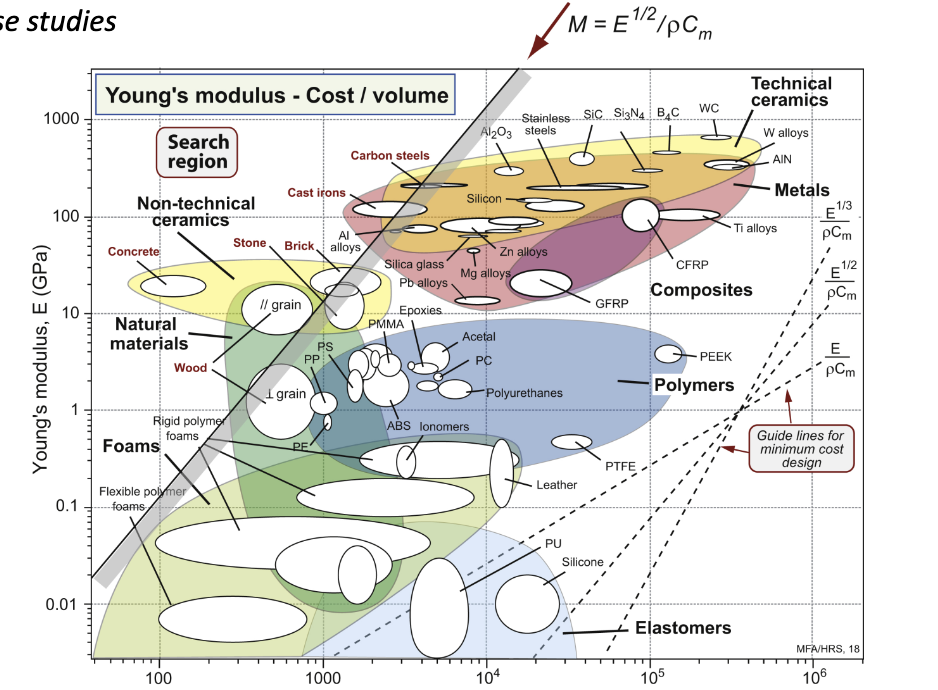
cost: structural materials for buildings (floor beam)

constraints: length L, square cross-section, maximum deflection δ, stiffness S

objective: minimize cost

free variables: material, area of cross-section

material index of light, stiff beam; adding cost:

C = mC_m = ALρC_m

leads to material index M = E^½/(ρC_m)

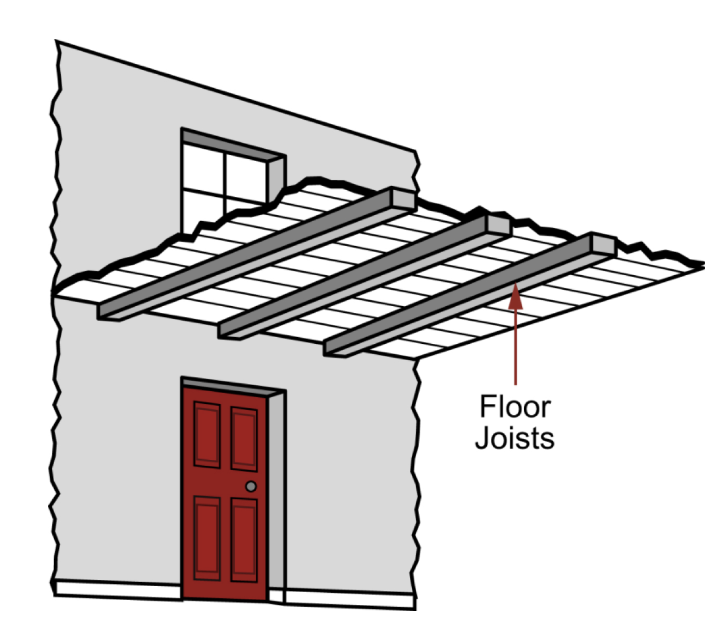
carbon steel, cast irons, brick, stone, wood || grain, wood ⊥, grain, concrete

list the seven best stiff-low cost materials using M_b below