9.2 : Angular Motion

angular motion

• movement of a body in a circular path about an axis of rotation

• e.g

  • a gymnasts whole body will rotate around the high bar

3 axis of rotation

1. longitudinal

2. transverse

3. frontal

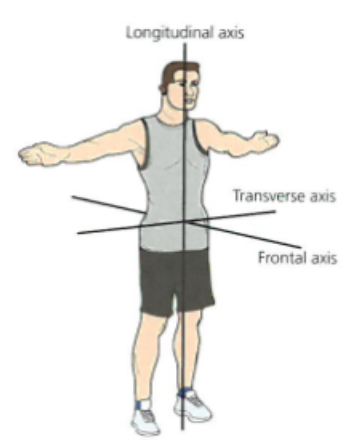
longitudinal axis

• head to toe through COM

• transverse plane of motion

• rotation

  • imagine a globe

• e.g → pirouette in ballet

transverse axis

• left to right through COM

• frontal plane of motion

• adduction and abduction

  • imagine table football and the little players

• e.g → front somersault in gymnastics

frontal axis

• back to front through the COM

• transverse plane of motion

• flexion and extension

  • e.g bicep curl

radian

• angular motion is measured in radians

• a unit of measurement of the angle through which a body rotates

angular motion descriptors

• angular velocity

• moment of inertia

• angular momentum

angular velocity definition

• rate of change in angular displacement measured in radians per second

angular velocity equation

• angular velocity = angular displacement / time taken

• rad/s → radians per second

moment of inertia definition

• the resistance of a body to change its state of angular motion or rotation

moment of inertia equation

• Moment of inertia = sum of (mass x distribution of mass from the axis of rotation²) 

• Measured in kgm² 

2 factors that affect moment of inertia

• mass

• distribution of mass from the axis of rotation

remember eq

How mass affects moment of inertia

• the greater the mass of a body the greater the moment of inertia 

• Sports with a high degree of rotation or technical requirement are typically performed by athletes with low mass 

• Low mass → decreases moment of inertia and the resistance to change state of rotation, so athletes can start rotation,change the rate of rotation and rotation with relative ease

How distribution of mass about an axis of rotation affects moment of inertia

• The further the mass moves from the axis of rotation the greater the moment of inertia - (moves slower wants to become more stable) 

  • e.g arms out

• The closer the mass distribution from the axis of rotation decreases moment of inertia and resistance to change state of rotation - moves faster 

  • e.g tucking arms in

moment of inertia is high so ….

• resistance to rotation is high

• angular velocity is low

• rate of spin is low

moment of inertia is low so ….

• resistance to rotation is low

• angular velocity is high

• rate of spin is high

e.g a spin in ice skating

• E.g an ice skater performing a static spin on ice will manipulate body position to maximise the technicality of the spin and aesthetic appeal to judges 

• Spin around longitudinal axis 

  • Mass tucked in = decrease moment of inertia = increase angular velocity = rotate quickly 

  • Limbs away from the body = increase moment of inertia = reduce angular velocity = decrease rate of spin

angular momentum definition

• the quantity of angular motion possessed by a body

angular momentum equation

• Angular momentum = moment of inertia x angular velocity 

• Measured in kgm²rad/s 

how is angular motion created

• eccentric force being applied outside the bodies centre of mass

eccentric force

• An eccentric force is also known as torque 

  • Torque → a measure of the turning force (eccentric or rotational) applied to a body 

How is angular momentum generated

• To start rotating around an axis → angular momentum must be generated 

• Eccentric force or torque must be applied 

• The greater the size of the eccentric force applied the greater the quantity of angular momentum generated for the movement ( greater acceleration)

Angular Analogue of newton's first law of motion 

• A rotating body will continue to turn about its axis of rotation with constant angular momentum unless acted upon by an eccentric force or external torque 

conservation of angular momentum

• As moment of inertia increases , angular velocity decreases 

• Angular momentum once generated does not change throughout a movement 

• Angular momentum remains constant and is conserved 

• This means a performer can keep a rotation going for a long period of time 

Angular motion in the take off of a spin in ice skating

1. the ice skater generates angular momentum by applying an eccentric force from the ice to their body 

2. The ice skater starts a rotation about the longitudinal axis 

3. Their distribution of mass is away from the longitudinal axis as their arms and legs are held away from the midline 

4. The moment of inertia is high and angular velocity is therefore low - go into the jump rotating slowly and with control 

Angular motion in flight of a spin in ice skating

• the ice skater distributes their mass close to the longitudinal axis as they tuck in their arms and legs 

• The moment of inertia is decreased and therefore angular velocity increases 

• They spin quickly , allowing several rotations in the time available in the air 

Angular motion in landing of a spin in ice skating

1. In preparation to land the ice skater distributes their mass away from the longitudinal axis , opening out their arms and one leg 

2. The moment of inertia is raised and angular velocity is reduced 

3. They decrease their rate of spin , increasing their inertia for landing and prevent over rotation 

4. As they land, the ice applies an external torque to remove the conserved quantity of angular momentum maintained throughout the jump to move away smoothly

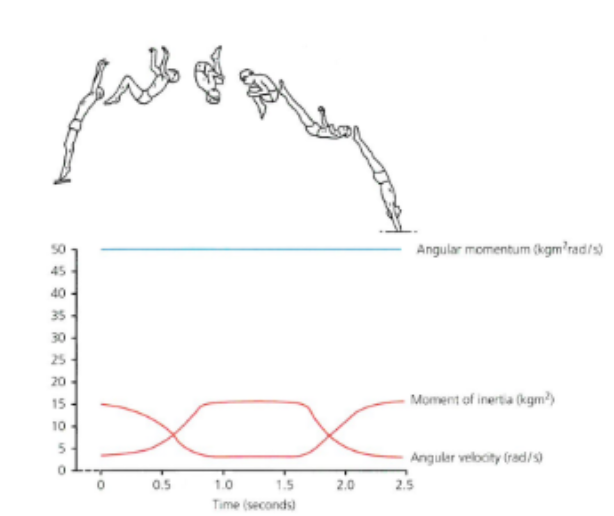
graph : diver diving from take off to landing → take off

• At take off the diver generate angular momentum by eccentric force from the springboard acting on the body and starts rotation about the transverse axis 

• The straight body position distributes mass away from the transverse axis

• the moment of inertia is high

• angular velocity is low

• diver rotates slowly and with control 

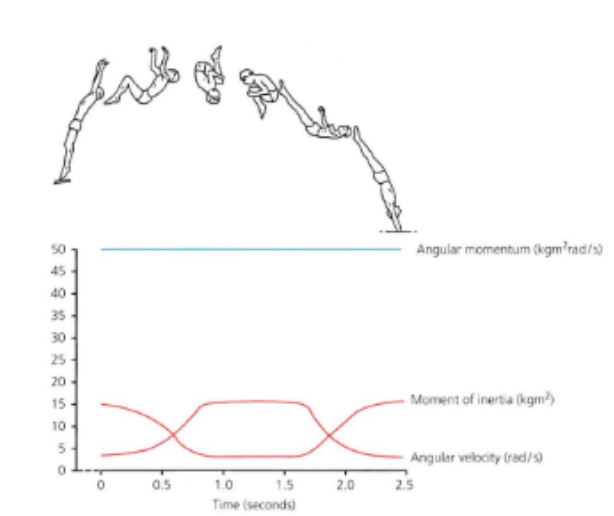
graph : diver diving from take off to landing → during flight

• During flight the divers body is tucked distributes mass close to the transverse axis

• moment of inertia is decreased

• angular velocity is increased

• diver rotates quickly

• enabling rotation during time in flight 

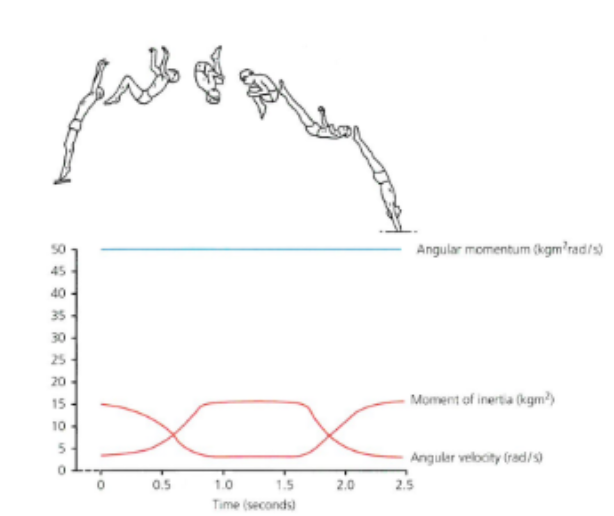
graph : diver diving from take off to landing → prep to land

• Preparing to land the divers straightened body position distributes mass away from the transverse axis

• moment of inertia increases

• angular velocity is decreased

• rate of spin decreases

• gaining control for entry to the water 

• Angular momentum is conserved throughout the momentum