Modelling with Algorithms

What is an algorithm?

Finite sequence of operations for solving a problem

What are the bin packing algorithms?

First-fit, pack each box into the first available bin, O(n²) complexity, heuristic

First-fit Decreasing, order boxes in descending order and apply first-fit algorithm, O(n²) complexity, heuristic

Full-bin method, look for combinations of boxers which fill a bin and pack them, the rest of the boxes put into combinations that come as close as possible to filling bins, not an algorithm as there may be different ways of packing full bins

What is the quick sort algorithm?

sorting algorithm, complexity O(nlog(n)), worst case O(n²)

take first number in list as pivot

rearrange all numbers less than or equal to the pivot to be left of the pivot in the order of arrival

rearrange all numbers greater than pivot to be right of the pivot in the order of arrival

box the pivot as it is now sorted

take the 2 sub-lists either side and repeat the steps, only if the lists have more than one item

continue until every sub-list contains one number

What is a graph?

A set of arcs/edges connecting nodes/vertices

What is a loop?

an arc with the same node at both ends

What is the order/degree of a node?

number of arcs incident on it (B has order 4, A has order 3 etc.), can be shown by an incidence matrix

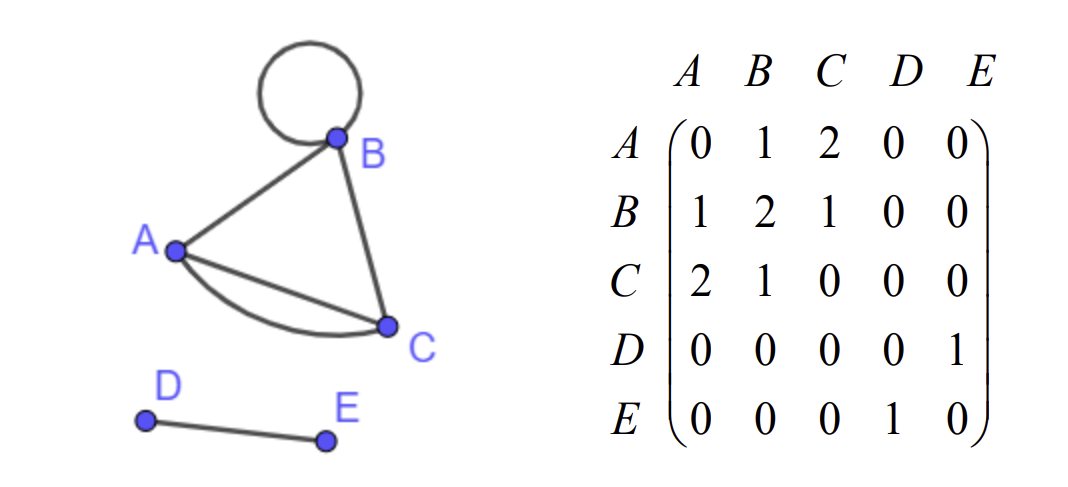
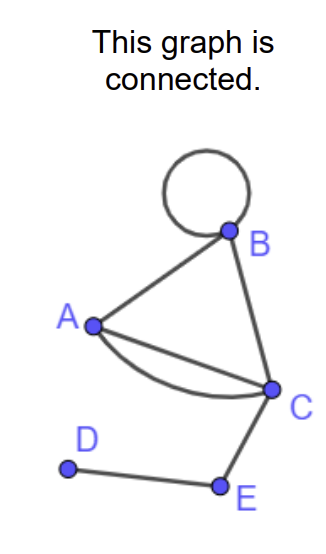
What is a connected graph?

a graph in which every node is joined directly or indirectly to each of the other nodes

What is a simple graph?

a graph with no loops and no multiple arcs

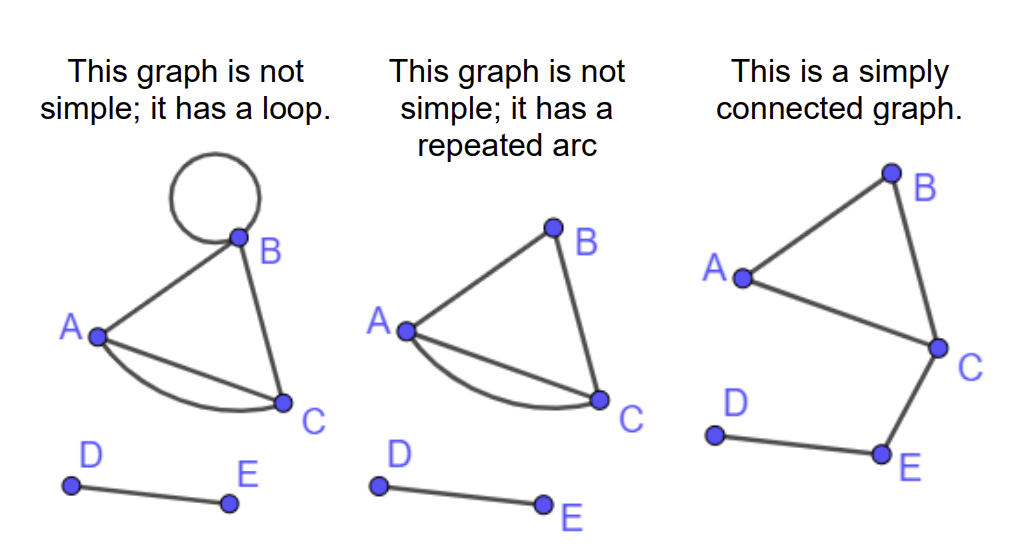
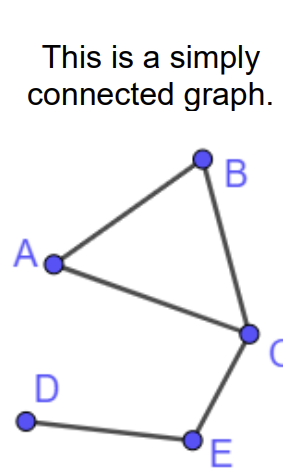
What is a simply connected graph?

A graph which is simple and connected, no loops or multiple arcs and all the nodes connected to one another directly or indirectly

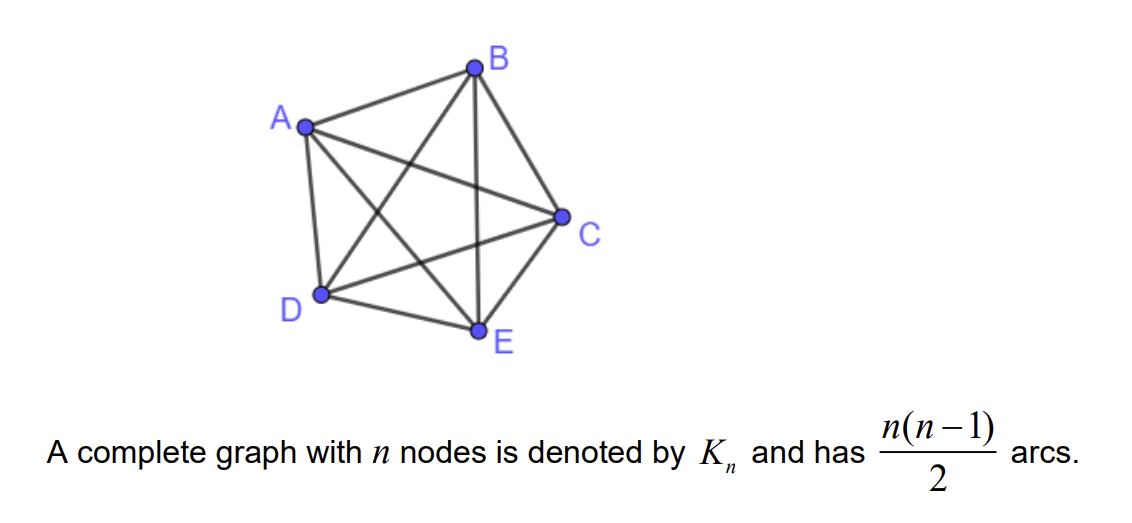
What is a complete graph?

Simply connected graph where every node is connected to one another, has the maximum possible number of arcs

connected graph with n nodes has n(n-1)/2 arcs

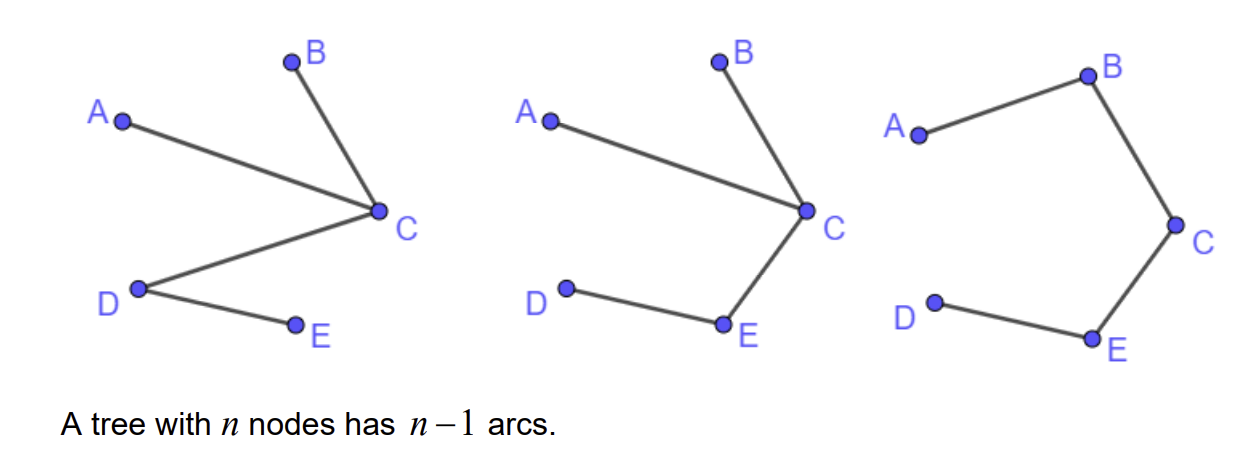
What is a tree?

A simple connected graph with no cycles

A tree with n nodes has n-1 arcs

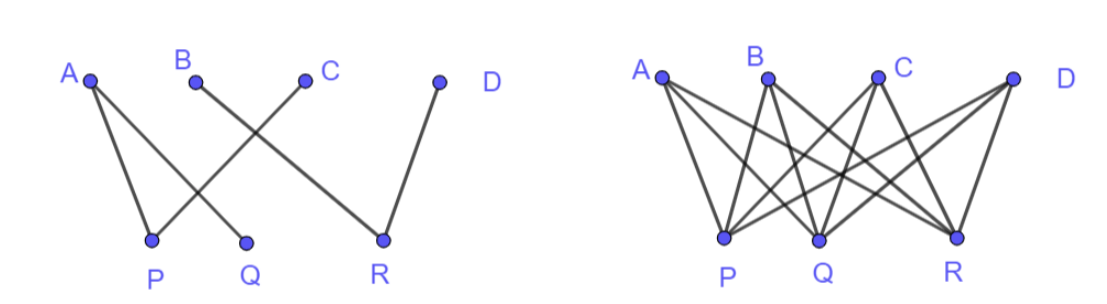
What is a bipartite graph?

A graph with nodes divided into two distinct sets, all arcs go from one node in one set to a node in the other set, nodes from the same set cannot be connected

a complete bipartite graph with m nodes in one set and n nodes in the other has mn arcs

What is a digraph?

a graph with one or more directed arcs, affects the incidence matrix

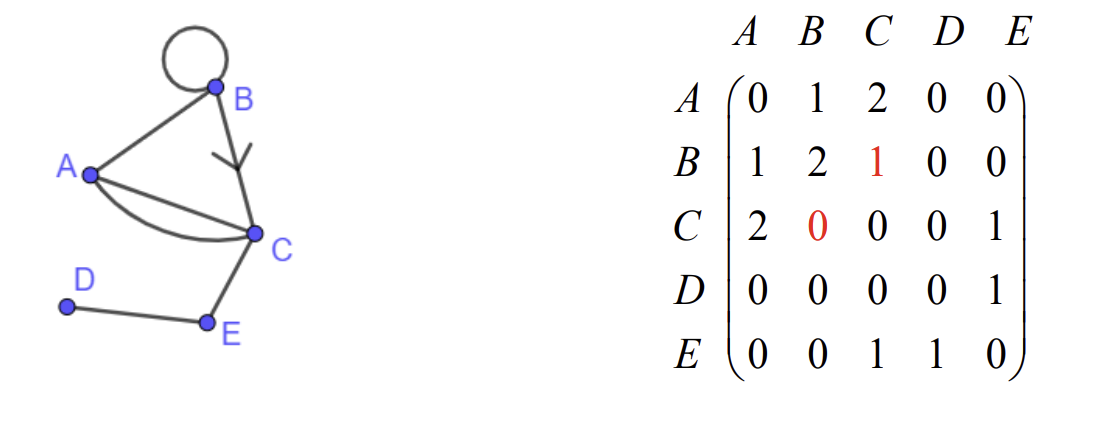
What is a network?

A weighted graph, weights associated with its arcs, can be represented by a table

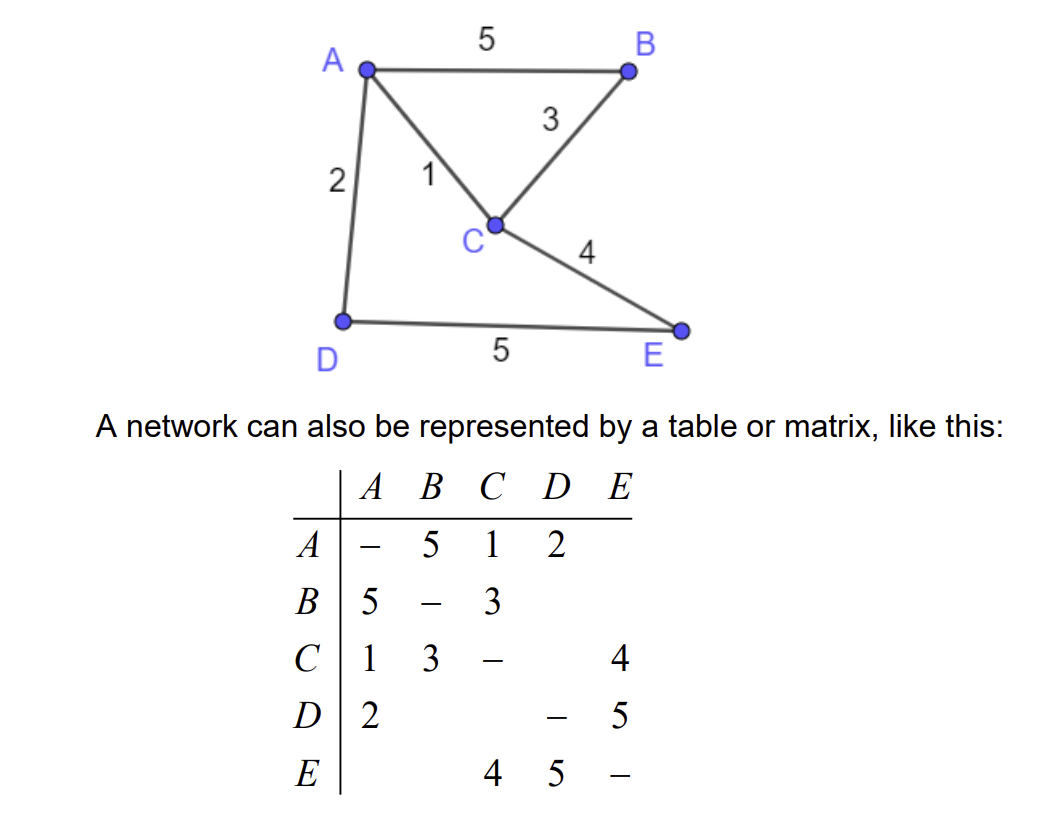
What is a minimum spanning tree?

A set of arcs for a network chosen from all the arcs that connects all the nodes so that the total weight of the arcs is as small as possible

What is Kruskal’s algorithm?

algorithm to find a minimum spanning tree, has complexity O(n²)

Selects the least weighted arc (shortest arc) of the network that does not link nodes that have already been linked directly or indirectly, repeat until each node is connected

What is Prim’s algorithm?

algorithm to find a minimum spanning tree, has complexity O(n²)

Select a start node and connect the nearest node (node that connects to current with least weight),

Connect nearest node that is not already connected to nodes in solution

Repeat until each node is connected

Can be done from a table,

Choose starting node and number column 1,

Cross out starting node row,

Pick smallest weight from column,

Number chosen node column and cross out row,

Repeat for new selection of columns

Will Kruskal’s and Prim’s algorithm give the same minimum spanning tree?

if there is only one minimum spanning tree yes, otherwise they could give different results, as well as different results for different starting nodes for prim’s algorithms

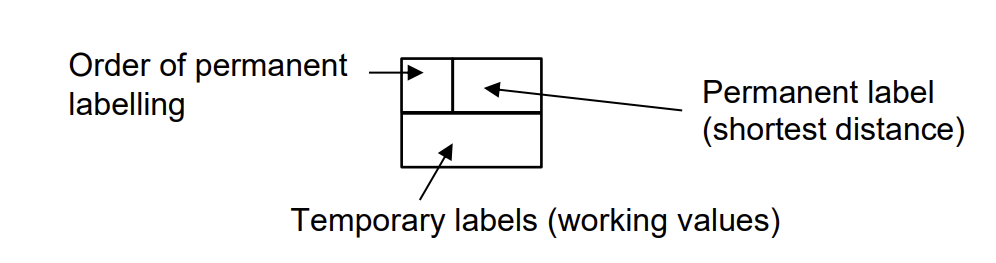
What is Dijkstra’s algorithm?

finds shortest path between two nodes in an undirected network, complexity O(n²)

Label start node 0

Put temporary labels on all connected nodes with their distances

Select node with smallest temporary label and make it permanent

For new node put temporary labels on all connected with distance at E + distance from E

Repeat until all nodes have permanent labels

Find shortest path starting from destination node and working backwards where difference between nodes = arc length

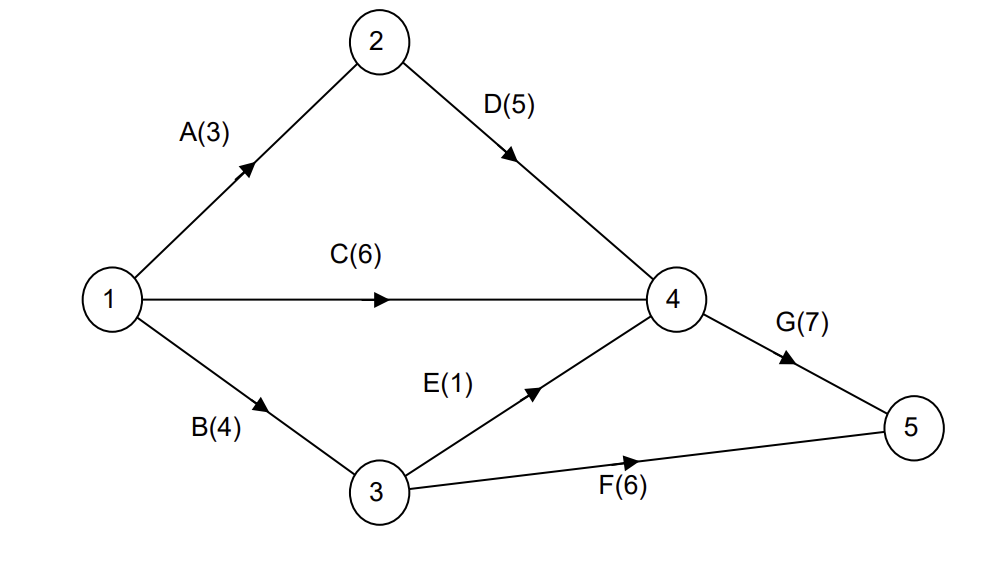
What is Critical path analysis?

find the minimum completion time of a project and the critical activities (longest path through the directed network)

find the early and late event times for events,

early found with a forward pass (earliest possible times to reach an event)

latest found with a backward pass (latest time possible that each event can take place if the project still finishes on time)

What is an activity network?

network where nodes represent events and arcs represent activities which link events with weights equal to their duration

What is a dummy activity?

unlabelled arc with zero duration to make the network fit the requirements

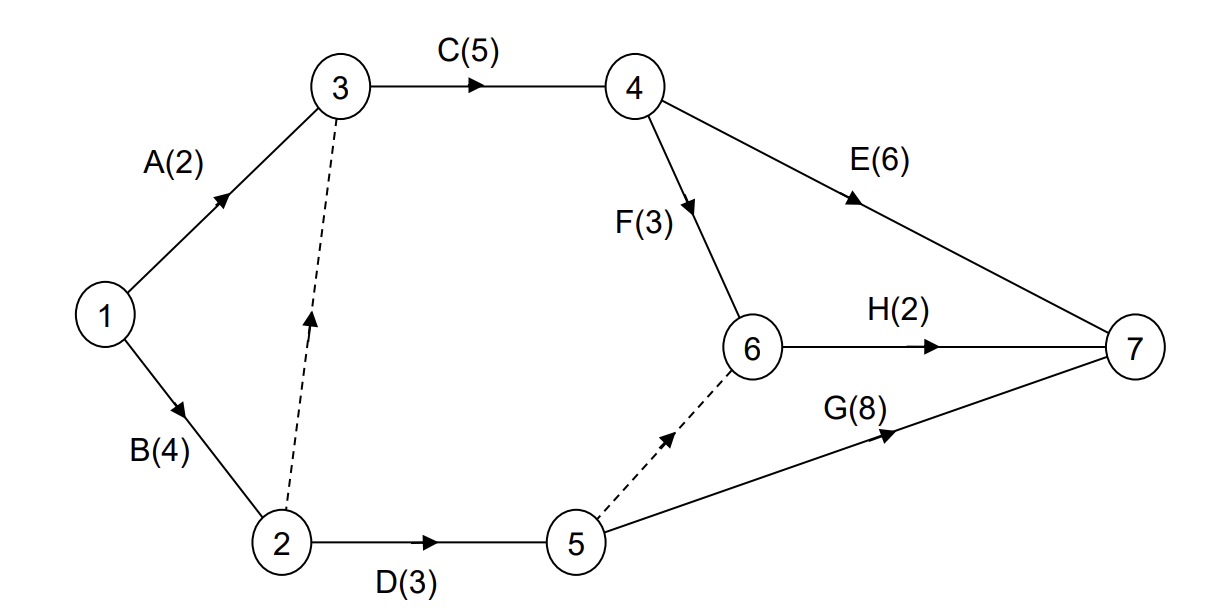
What is a critical activity?

activity that cannot start late without increasing the minimum project completion time, activity where the difference between late and early time is equal to its duration (zero float (total float))

What is the float (total float) for activity (i, j)?

(latest time j - earliest time i) - duration

What is the independent float for activity (i, j)?

(earliest time i - latest time j) - duration, or 0 if negative, means the float is independent of other activities

What is the interfering float for activity (i, j)?

total float - independent float, means the float shared between activities

What is a cascade chart?

diagrammatic representation of a project useful in assigning workers to tasks and making use of floats

What is a resource histogram?

diagrammatic representation of a project useful in assigning workers to tasks and making use of floats

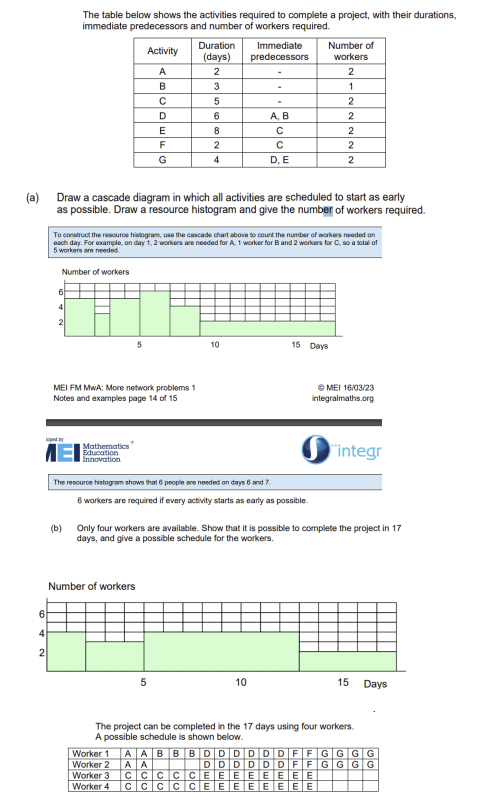
What is network flow?

network where weights are the capacity of the arcs

S is the source node,T is the sink node

only arcs connected to S and T have to be directional

Flow into a node = flow out of a node

Total flow = minimum cut = flow out of source = flow into sink

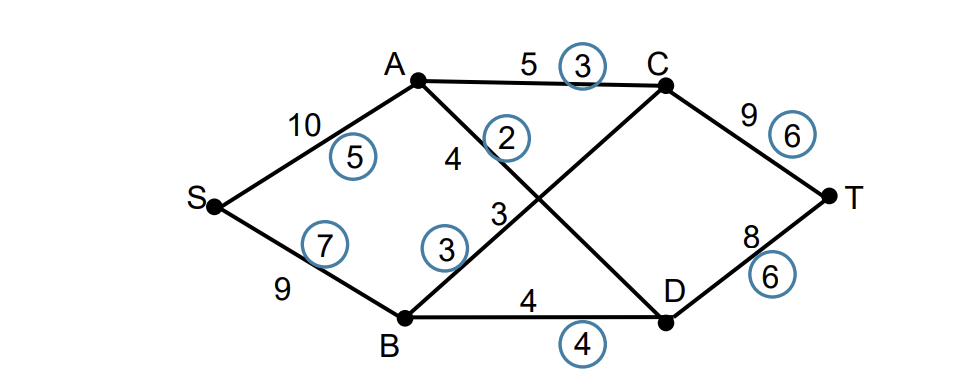
What is a saturated arc in a network flow?

flow through an arc = arc capacity

What is a cut?

a partition of the set of vertices of a network into two sets

source S and sink T in different sets

capacity of a aaaaaaaaaacut = sum of capacities of arcs that join sets S to T

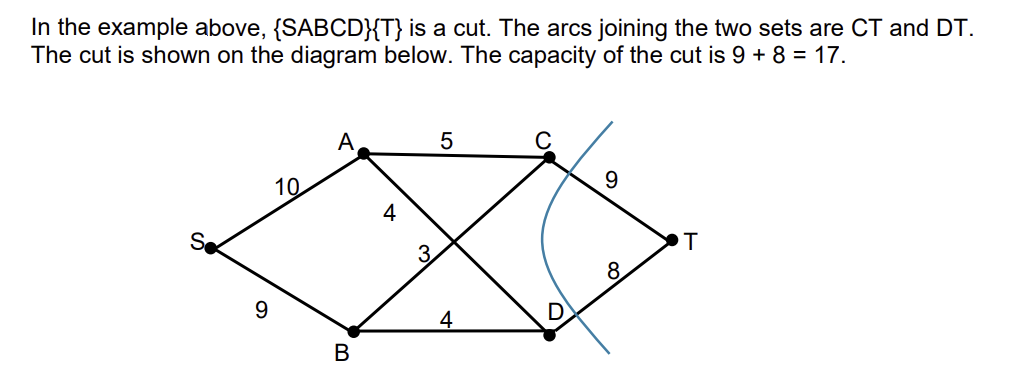
What is the maximum flow / minimum cut theorum?

maximum flow = minimum cut

What are the steps to solving a network flow problem when there are multiple sources and/or sinks?

Add a super source node connecting each source node,

Add a super sink node connecting each sink node

What is a constraint specific to an integer programming problem?

variables in the problem are integers

What are the steps to formulate a linear programming problem?

Define variables

Find constraints

Find objective function

How can a linear programming problem be solved graphically?

constraints drawn on the graph

region that satisfies all constraints is the feasible region

solution always occurs at a vertex

Objective line method:

draw objective line and move it across the page until the last vertex intersected (maximise problem) or the first vertex intersected (minimise problem)

Vertex checking method:

each vertex substituted into the objective function to find the optimal value

What is a step specific to solving an integer programming problem?

testing integer values around the solution found if not already an integer

choose values for x and find the minimum y values within the feasible region

for three variables test values around the vertex

What is the form of constraints required for simplex method?

augmented form, constraints contain slack variables that are non-negative

What are the steps for a simplex question?

Rewrite constraints in augmented form

Set out initial tableau

Carry out pivots:

Most negative element in objective row is pivot column (most positive for minimise problem)

Use ratio test to choose pivot element from pivot column (theta value)

Divide pivot row by pivot element

For every other row add or subtract multiples of the pivot row so every element in pivot column besides pivot element is zero

Repeat steps until all elements in objective row are positive or zero (negative or zero for minimise problem)

What does the simplex method do?

Finds the optimal solution to a linear programming problem

Traverses the vertices of the intersections of the constraints of the problem

Traversal is optimised to always take the vertex that is furthest from the origin for a maximise problem (the largest negative in the objective row), (for minimise the closest point to the origin is taken (largest positive in the objective row))

What are basic and non-basic variables for simplex solutions?

basic variables are in the basic solution, value is not 0 (in variable column all rows are zero except for one which has the value one)

non-basic variables are not in the basic solution, value is 0 (column is not like a basic variable column)

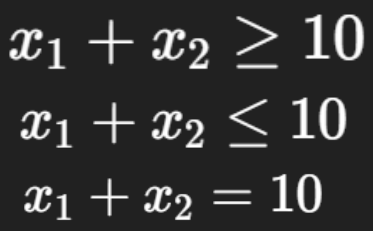
What is the augmented form for these constraints?

<=: + slack variable

>=: - slack variable + artificial variable

=: + artificial variable OR split into <= and >= constraints and deal with appropriately

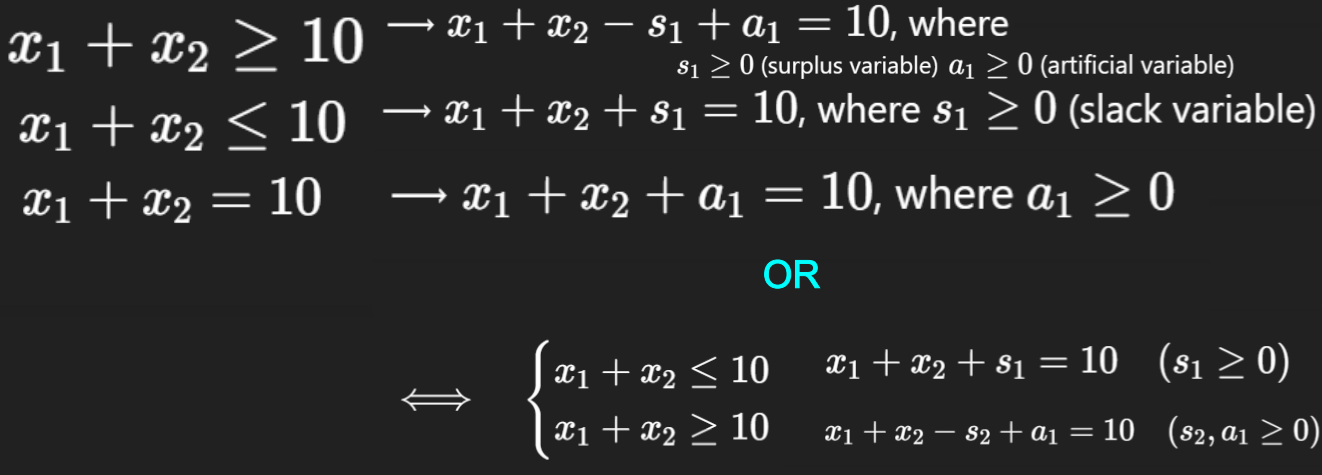
How to solve a two step simplex problem?

Rewrite constraints in augmented form

Sum of artificial variables = Q

Second objective function Minimise Q

Set out initial tableau

Carry out pivots for second objective function:

Most positive element in objective row is pivot column

Use ratio test to choose pivot element from pivot column (theta value)

Divide pivot row by pivot element

For every other row add or subtract multiples of the pivot row so every element in the pivot column besides pivot element is zero

Repeat steps until all elements in objective row are negative or zero

Remove second objective row (Q row) and remove artificial variable columns

For remaining table carry out pivots for first objective function:

Most negative element in objective row is pivot column (most positive value for minimise)

Use ratio test to choose pivot element from pivot column (theta value)

Divide pivot row by pivot element

For every other row add or subtract multiples of the pivot row so every element in pivot column besides pivot element is zero

Repeat steps until all elements in objective row are positive or zero (negative or zero for minimize problem)

For a two stage simplex problem are there any feasible solutions until Q is minimised?

No, the artificial variables must be non-basic (=0)

How can a shortest path problem be re-formulated as a linear programming problem?

Shortest path, Dijkstas’s algorithm

Each arc given a variable e.g. arc between node B and E is BE, there is also an arc EB which is different from BE

Each variable is an indicator variable (1 or 0)

Every arc has the opposite except for the start and end nodes eg. EB and BE, but if a is start node only AB as BA goes towards the start node

The length of the path is to be minimised, sum of the variables multiplied by their corresponding weights

Two types of constraints:

Constraints to ensure one arc out of start node and one arc into end node e.g. AB + AC = 1 where A is the start node

Constraints to ensure if a path arrives at a vertex then it leaves the vertex, sum of arcs into node - sum of arcs out of node = 0 e.g. AB + DB + EB - BD - BE = 0 for node B

Finally constrains on each variable to be <= 1, this prevents them taking any value, cannot be used to assign their distance as it is fixed, ensuring they are indicator variables

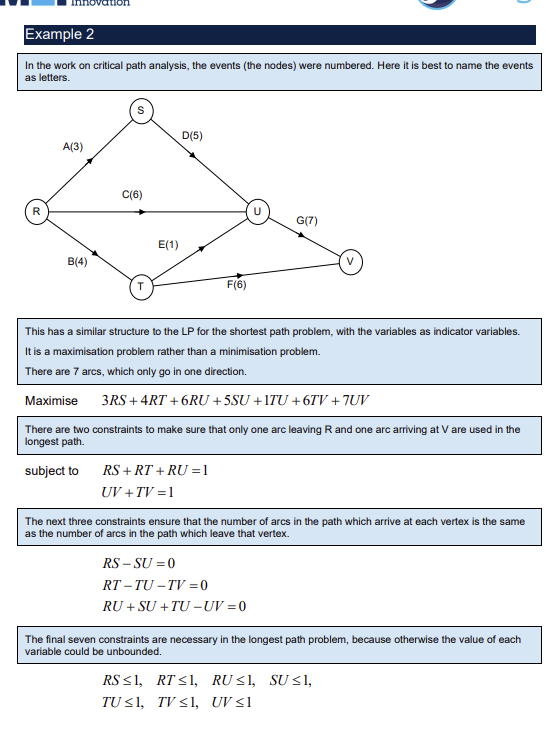
Howe to re-formulate a longest path problem into a linear programming problem?

For a directed network with no cycles longest path is the critical path

Every arc given a variable e.g. arc between events R and S is RS

Each variable is an indicator variable ( 1 or 0 )

Arcs that are directional can only have one arc variable e.g. RS not SR

Length of path is to be maximised, sum of the variables multiplied by their weights

Two types of constraints:

Constraints to ensure one arc out of start node and one into end node e.g. RS + RT + RU = 1 where R is the start node

Constraints to ensure number of arcs entering a vertex = number of arcs leaving that vertex, sum of arcs into node - sum of arcs out of node = 0

Finally constraints on each variable to be <= 1, this prevents them taking any value, cannot be used to assign their distance as it is fixed, ensures they are indicator variables

How can a maximum flow problem be re-formulated as a linear programming problem?

Every arc given a variable, arcs between nodes can have two variables unless directed, arcs at source and sink nodes are directed e.g. SA, no AS as S is the source node

Every arc constrained to be <= to its maximum flow e.g. SA <= 10

Maximum flow is to be found and so objective function can be to maximise the flow of any cut, typically the flow of the cut {S}{…..T} is used (the flow out of the source) e.g. SA + AB

The constraints are to ensure the flow into a node is the same as the flow out of a node, sum of arcs into node - sum of arc out of node = 0 e.g. SA + CA + DA - AC - AD = 0

How to reformulate a matching problem as a linear programming problem?

For a bipartite graph or its adjacency matrix, it can be shown which elements from the two sets can be matched in pairs

Matching problem is to find the maximal matching, maximum number of matches

A complete matching is where every element from both sets is matched

Each arc given a variable name they are indicator variables (1 or 0)

Objective function is to maximise the sum of the variables, the largest number of matches

Two types of constraints:

Ensures each node from set 1 only goes to one other node of set 2

Ensures each node from set 2 only receives one other node of set 1

e.g. set 1{A linked to U X and Y}, set 2 {U linked to A and Z}, constraints for A and U, AU + AX + AY <= 1, AU + AZ <= 1

<= 1 used for constraints as it may not be possible to match every node, = sign can be used for a complete bipartite graph

Finally each variable constrained to be <= 1, ensures they are indicator variables

How to re-formulate an allocation problem to a linear programming problem?

For a bipartite graph or distance table, allocation problems are a matching problem with weighted matchings (arcs)

Each arc given a variable name, they are indicator variables (1 or 0)

Objective function is to maximise or minimise the sum of the variables multiplied by their corresponding weights

The constraints are to ensure each node from set 1 is connected to exactly one node from set 2 and ensure each node from set 2 is connected to exactly one node from set 1

e.g. set 1 {A linked to U,V and W} set 2{U linked to A and B} AU + AV + AW <= 1, AU + BU <= 1

= sign can be used for constraints if graph is completed

Each variable constrained to be <= 1, ensures they are indicator variables

How can a transportation problem be re-formulated as a linear programming problem?

Minimises the cost of moving goods from a set of sources to a set of destinations where each source could supply multiple destinations (bipartite graph)

Arcs given variable names

Variables given non negative constraints, e.g. AB>= 0

Variables given any extra constraints e.g. transportation capacity of a route AB <= 50, almost always won’t have this though

Constraints ensure each source node output is maximum, ensures each destination node is maximum

e.g.

AP + AQ + AR <= 800 where A is a source node with capacity 800

AS + BS + CS <= 400 where S is a destination node

= signs can be used in constraints if completed bipartite graph or weight table and total output from sources = total input at destinations