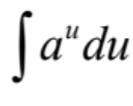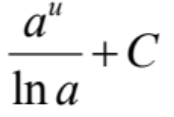AP Calc BC formula quiz
0.0(0)
Card Sorting
1/48
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
49 Terms
1
New cards
definition of e
\
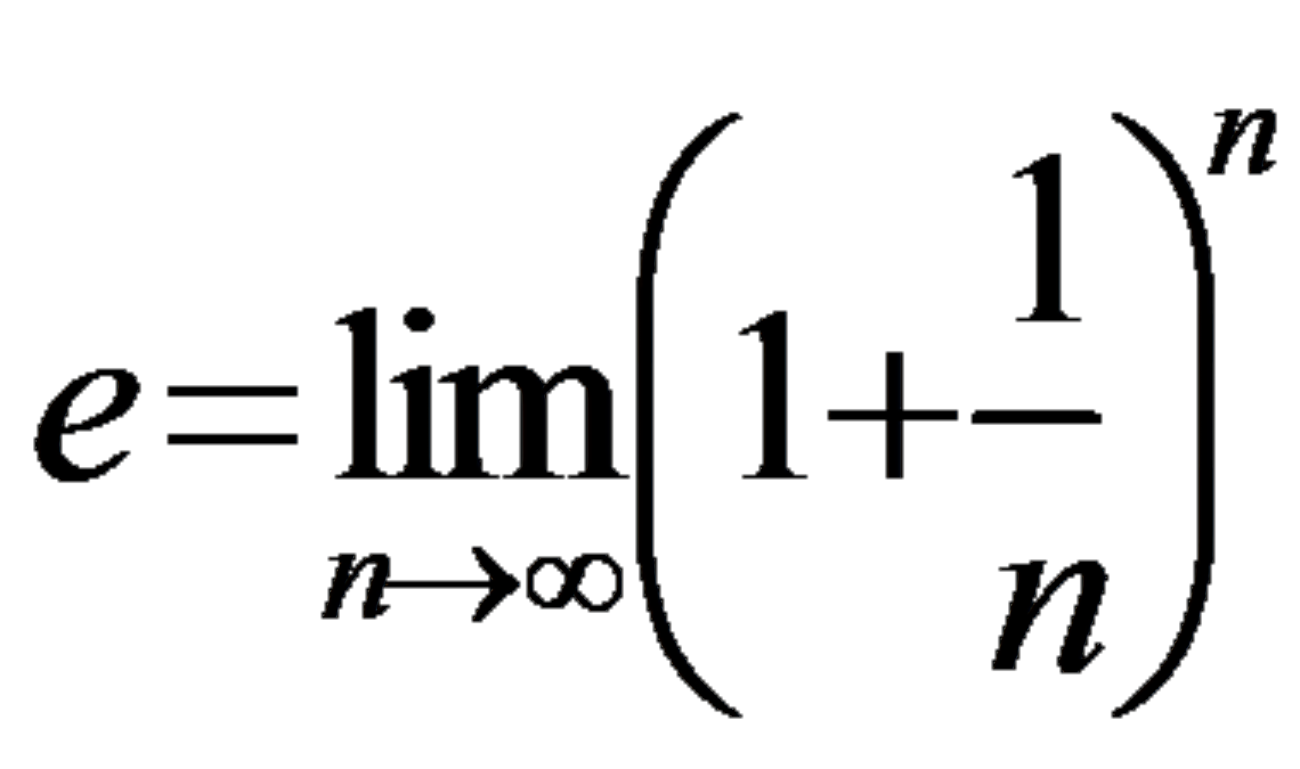
2
New cards
definition of absolute value
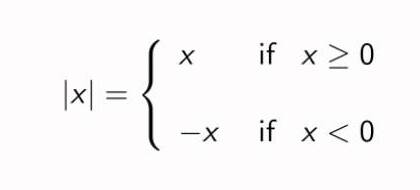
3
New cards
definition of the derivative

4
New cards
alternative definition of the derivative
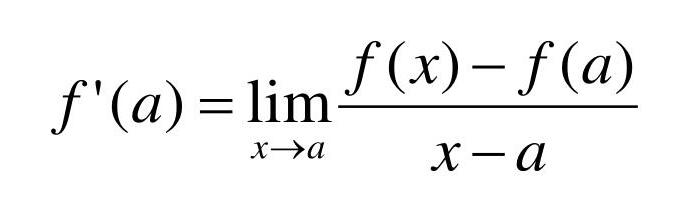
5
New cards
definition of continuity
\

6
New cards
average rate of change of f(x) on \[a,b\]
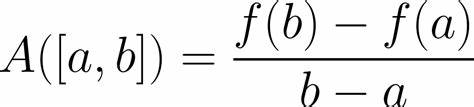
7
New cards
intermediate value theorem
if *f* is continuous on \[*a*,*b*\] and *k* is any number between *f(a)* and *f(b*), then there is at least one number *c* between *a* and *b* such that *f(c) = k*
8
New cards
what does d/dx \[c\] equal?
= 0
9
New cards
derivative product rule
d/dx \[*f(x)g(x)*\] = *f’(x)g(x)* + *f(x)g’(x)*
10
New cards
chain rule
d/dx (*f(g(x)*)) = *f’(g(x))* \* *g’(x)*
11
New cards
power rule
\
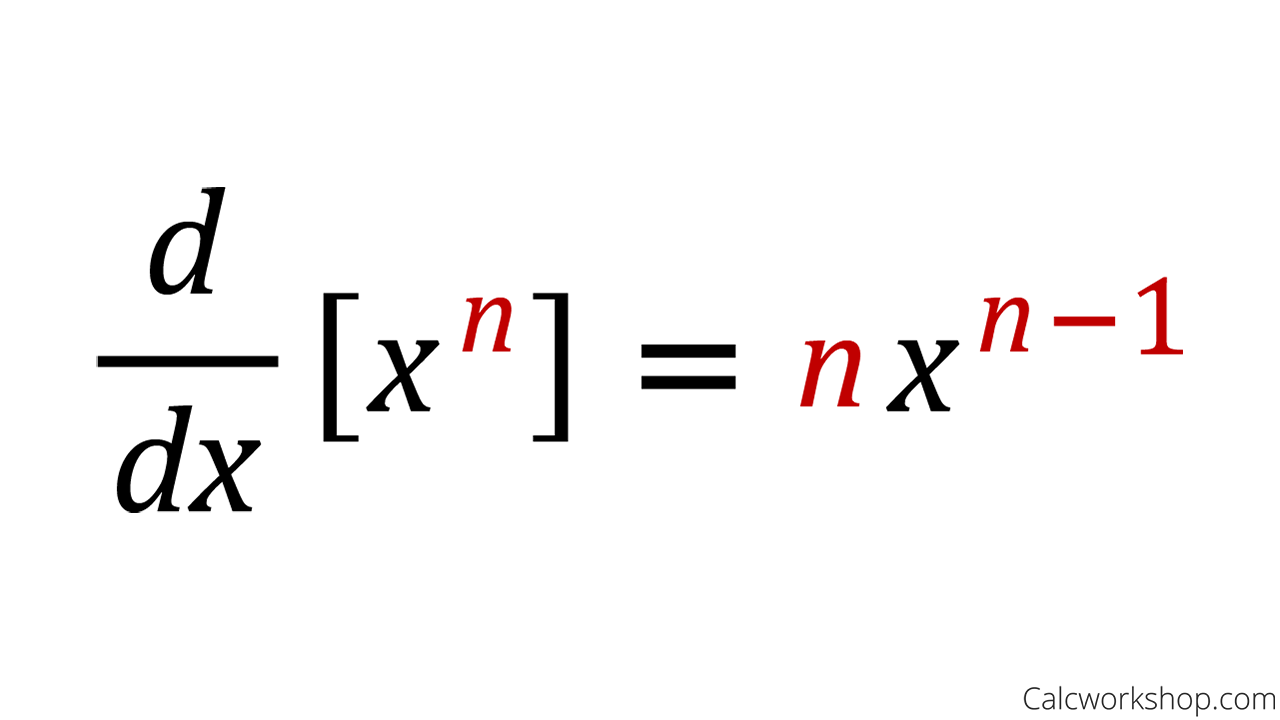
12
New cards
quotient rule
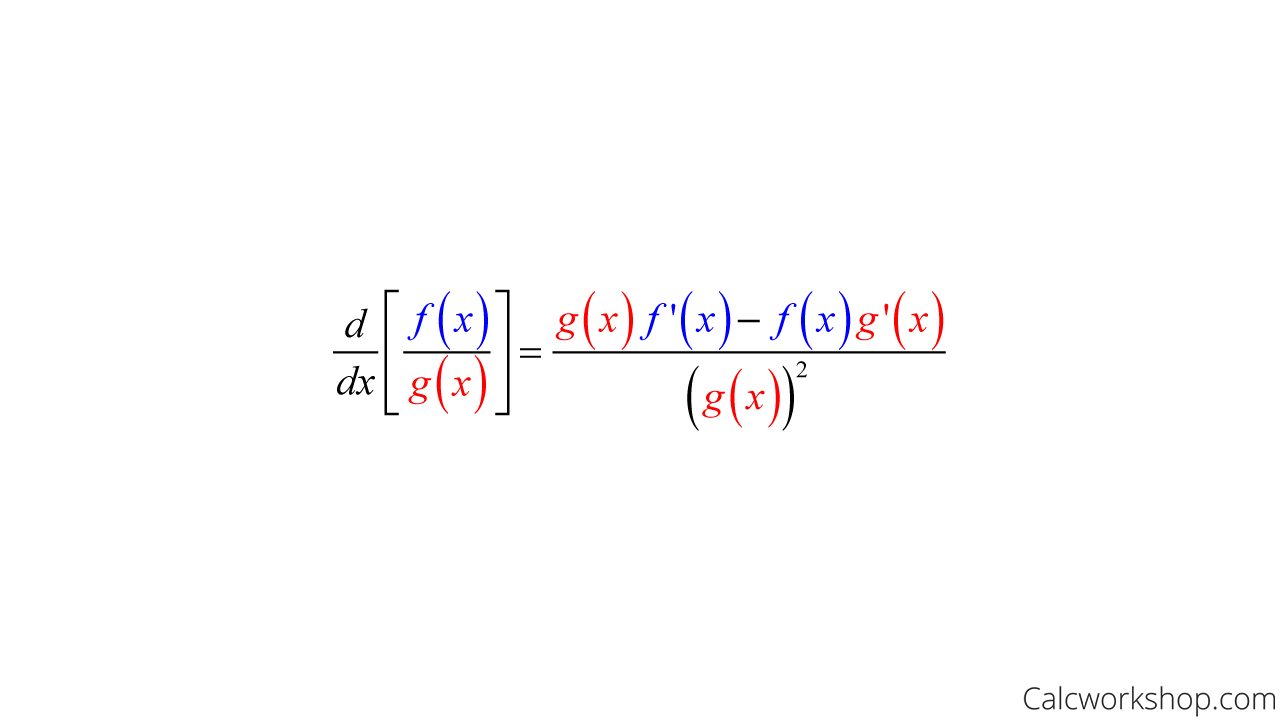
13
New cards
d/dx \[sin *u*\]
= cos *u* du/dx
14
New cards
d/dx \[cos *u*\]
= - sin *u* du/dx
15
New cards
d/dx \[tan *u*\]
= sec^2(*u*) du/dx
16
New cards
d/dx \[sec *u*\]
= sec *u* tan *u* du/dx
17
New cards
d/dx \[csc *u*\]
= -csc *u* cot *u* du/dx
18
New cards
d/dx \[cot *u*\]
= - csc^2 (*u*) du/dx
19
New cards
Rolle’s Theorem
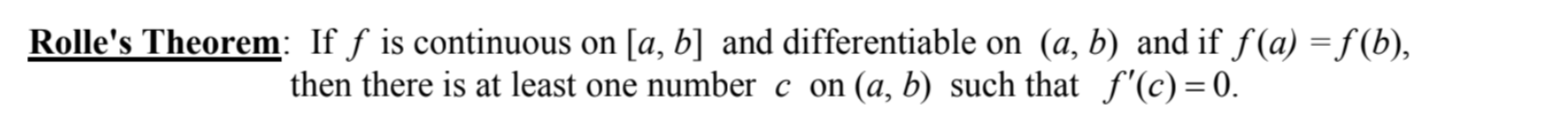
20
New cards
Mean Value Theorem (MVT)
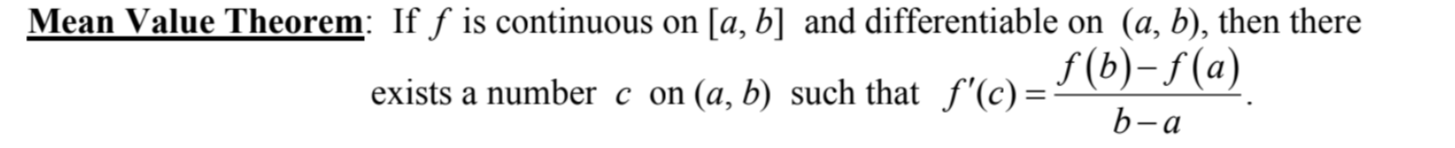
21
New cards
definition of a critical number

22
New cards
definition of increasing functions

23
New cards
definition of decreasing functions

24
New cards
Test for Increasing and Decreasing functions

25
New cards
First Derivative Test
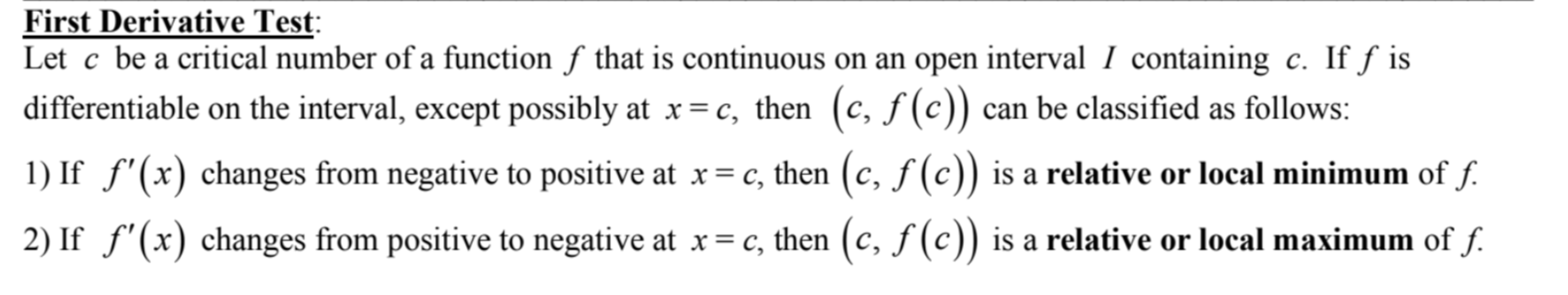
26
New cards
Second Derivative Test

27
New cards
definition of definite integral
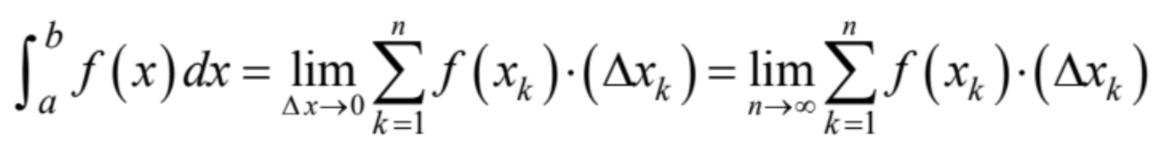
28
New cards
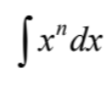
integral of …
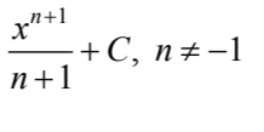
29
New cards
∫cos u du
sin u + c
30
New cards
∫sin u du
-cos u + c
31
New cards
∫sec²u du
tan u + c
32
New cards
∫sec u tan u du
sec u + c
33
New cards
∫csc²u du
-cot u + c
34
New cards
∫csc u cot u du
-csc u + c
35
New cards
first fundamental theorem of calculus

36
New cards
second fundamental theorem of calculus
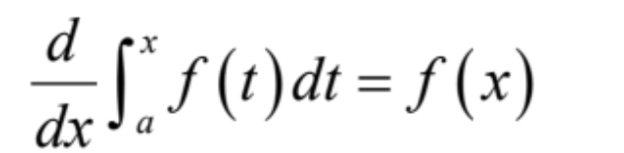
37
New cards
integral chain rule
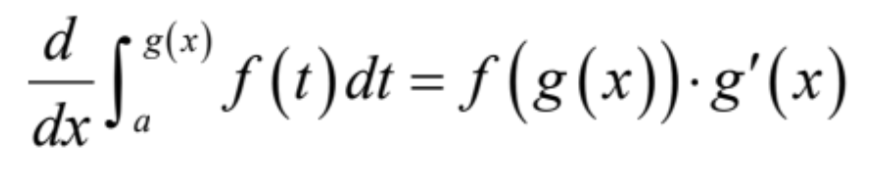
38
New cards
average value of f(x) on [a,b]
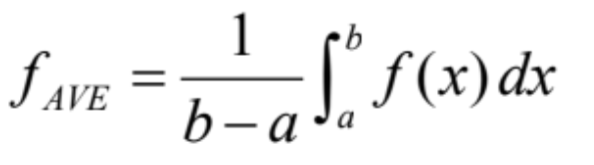
39
New cards
derivative of inverse function d/dx [(f^-1)(u)]

40
New cards
d/dx [ln u]
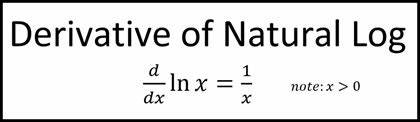
41
New cards
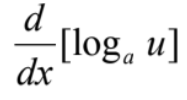
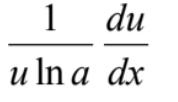
42
New cards
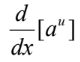
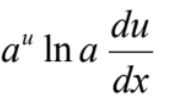
43
New cards
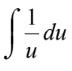
ln |u| + C
44
New cards
∫tan u du/dx
-ln |cos u| + C
45
New cards
∫sec u du/dx
ln |sec u tan u| + C
46
New cards
∫cot u du/dx
ln |sin u| + C
47
New cards
∫csc u du/dx
-ln |csc u + cot u| + C
48
New cards
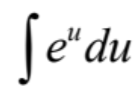
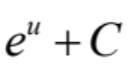
49
New cards