SW2 Midterm 2 BST

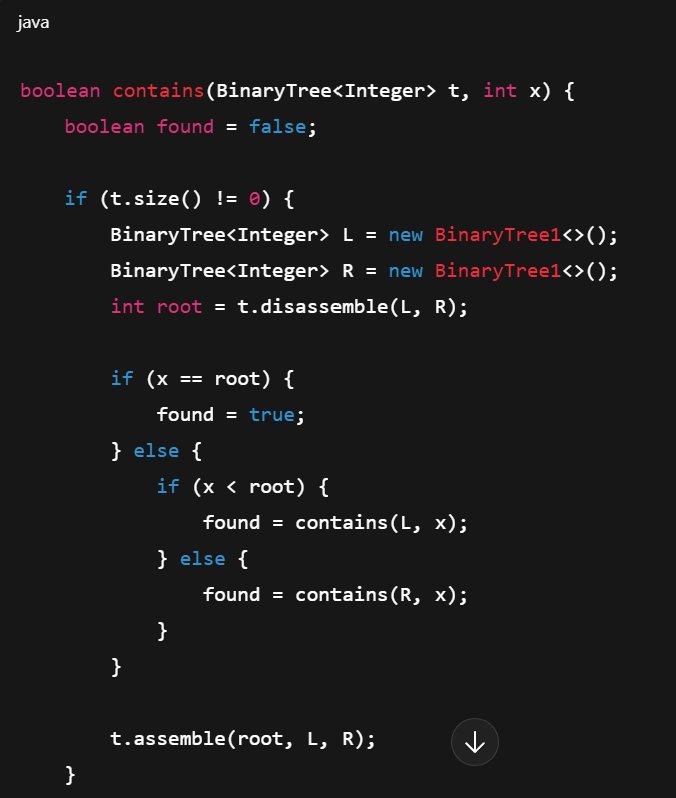
contains Algorithm (searching in BST)

returns a binary tree t
if t is empty x is not found
r is the root, of t then found

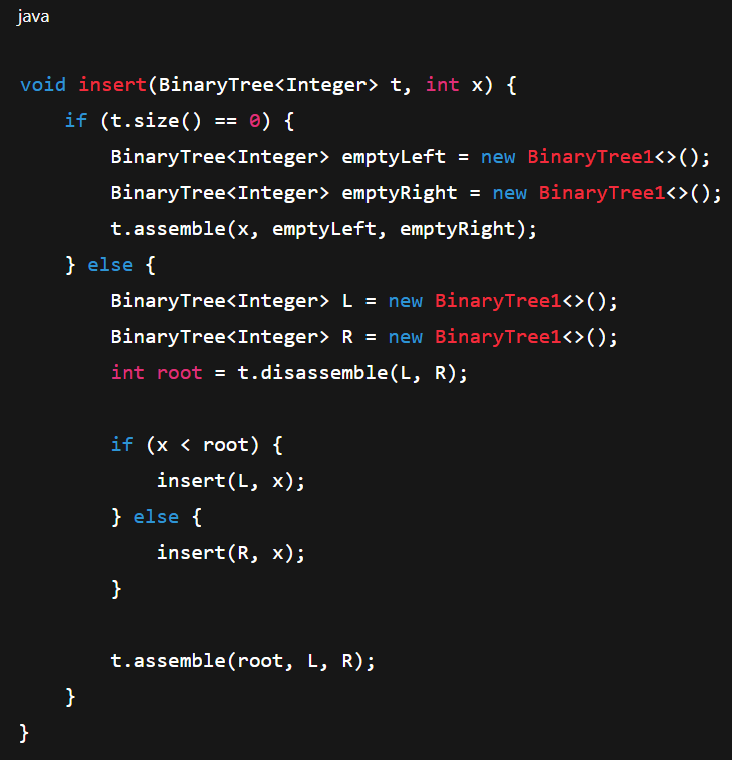
Insert Element  in  BST

if tree is empty, assemble single node tree with x
otherwise compares x with r and resemble recursively

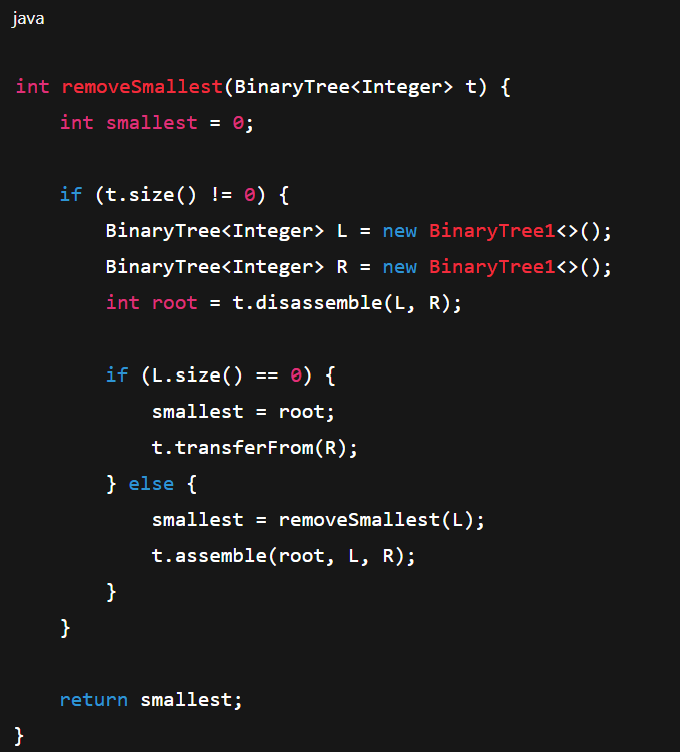
removeSmallest(HelperFunction)

located in the left most side of the tree

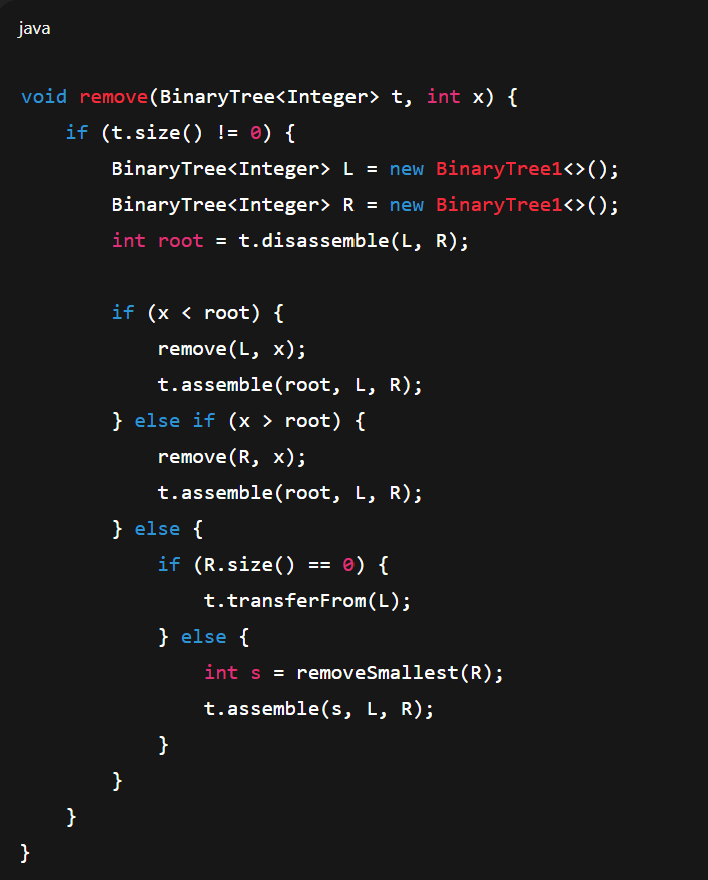
remove (Delete specific element from BST)

3 cases: deleting leaf, deleting a single child, deleting from a node with two children
O(h) complexity worst case 

Height (Tree Height)

Mathematical:

-empty tree: 0 
-non empty Tree = 1+Math.max(height(L), height(R))

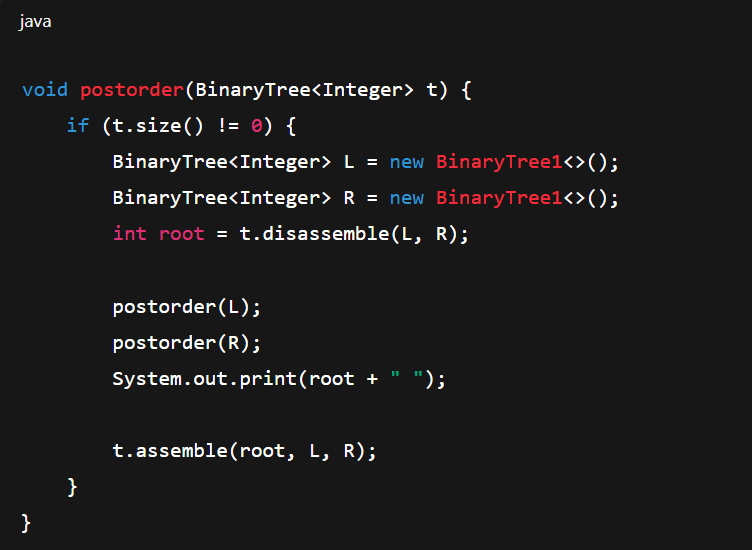
size (counting all nodes)

empty: 0
nonempty: 1 + size(leftTree) + size(rightTree)

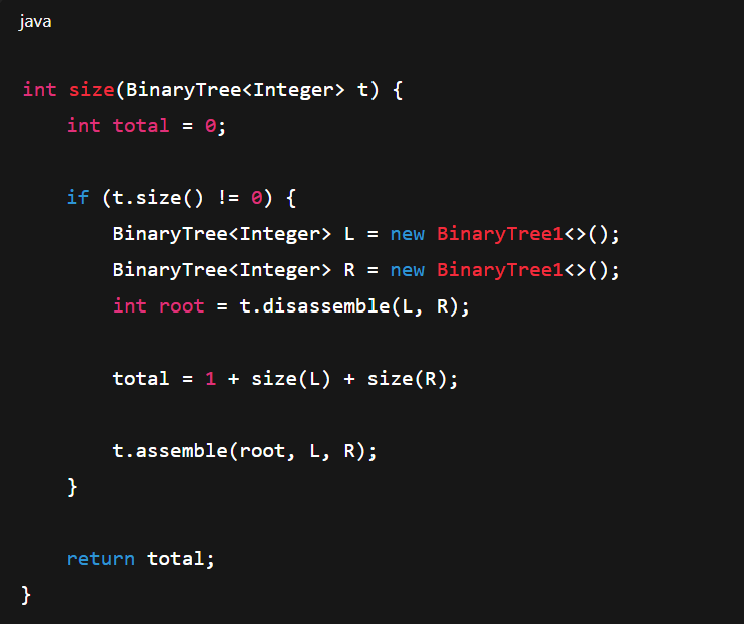
PreOrder

root>left>right
Traversal for copying or printing the tree structure

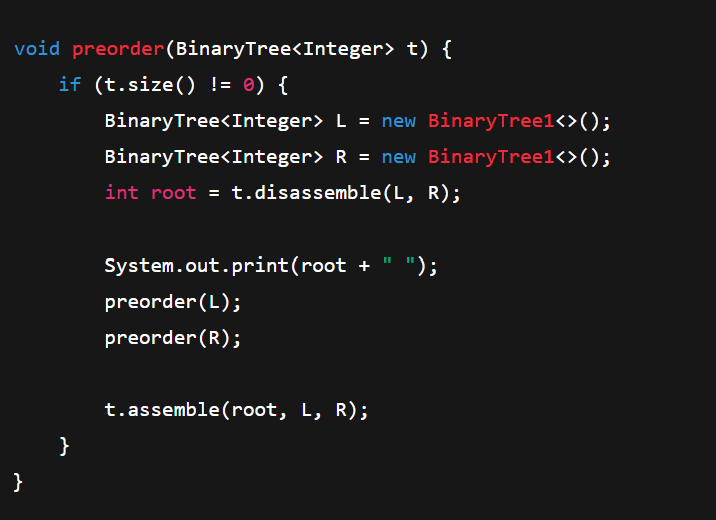
In Order Traversal

Left>Root>Right
getting keys from BST in sorted order

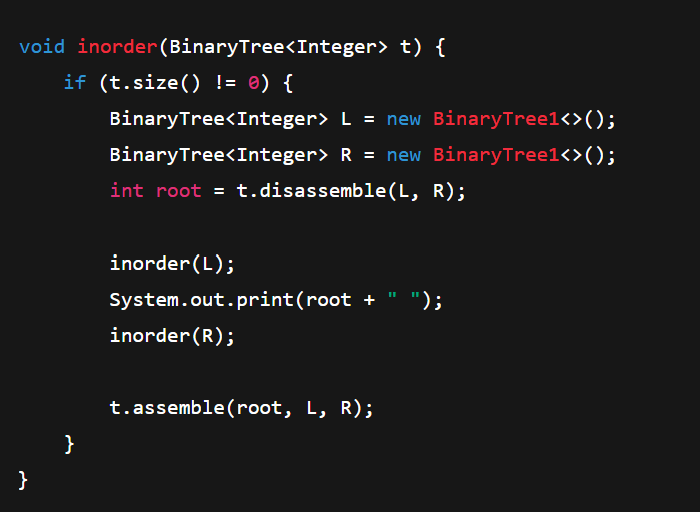
Post-order

Order: left>right>Root

Traversal for deleting a subtrees/tree, children first (need to delete the children first before deleting the root)

BST order

root k > left subtree

root k < right subtree

Math.max(a,b)

-Returns greater of two numbers
-Used for height

Mathematical size of non empty Tree

b.size = 0

Characteristics of Binary Trees

size, labels, height, follow recursive structure, do not have to be balanced

Assemble (T root, Binary Tree<T> left, Binary Tree<T> left, )

Kernal method: combines root, and the 2 subtrees

T disassemble (BinaryTree <T> left, BinaryTree<T>right)

returns the root value and breaks apart the left and right subtrees, and clears the original tree

T root()

returns the root (so long as its nonempty)

T replaceRoot (T x)

replaces the root with x (and returns old root) such that it is a nonempty Tree

Iterator<T> iterator()

return an iterator that visits labels in-order by contract