Physics Unit 3 and 4 QCAA

Vectors - x component formula (velocity)

Vx=Vcos(theta)

Vectors - y component formula (velocity)

Vy=Vsin(theta)

How do you add and subtract vectors?

Tip to tail, which gives a resultant vector.

What is a simple definition of projectile motion.

The motion of an object projected into the air and moving under the influence of gravity.

What does SUVAT stand for?

S=Displacement

U=Initial velocity

V=Velocity

A=Acceleration

T=Time

What assumptions are applied to physics projectile motion?

It is assumed there is no air resistance or drag force to consider.

Which value is a constant in both the x and y axis for SUVAT equations, what are the values?

Acceleration, in the x axis it is usually 0 and in the y axis it is usually 9.8m/s.

Which angle gives the largest horizontal displacement in projectile motion?

45

What is special about complementary angles in projectile motion?

Complementary angles give the same horizontal displacement.

Define the normal force.

The force that is perpendicular to the contact surface of the plane of motion.

How to find the perpendicular and parallel forces?

Using alternative angles, Fsin and Fcos

Define friction force.

Friction force is the force that opposes motion of objects traveling across a surface.

when traveling in a circle what does velocity do?

Velocity is constantly changing as it is a vector quantity, the magnitude may not change but the direction does. At all times the velocity is a tangent to the circle of motion.

Formula for velocity of uniform circular motion?

v=(2pir)/T

where

• v is the velocity

• r is the radius

• T is the time taken to complete a full revolution (the period)

If at all times velocity is a tangent to circular motion why does the object not fly away?

Centripetal acceleration

Formula for centripetal acceleration

a=V²/r

a = centripetal acceleration

v = the velocity

r = the radius

In which direction does centripetal force act?

Vectors point towards the centre of the circle of motion at all points.

Centripetal force equation

F=ma=(mv²)/r

F = force

m = mass

a = acceleration

v = velocity

r = radius

What is Centrifugal force?

A ficticious force in newtonian physics that appears to act on all objects in circular motion, acting away from the center around which the body is moving.

What is Newton’s description of gravitational attraction? (equation)

F=(GMm)/r²

F = force

G = gravitational constant (6.67×10^-11 Nm²/kg²)

M = Mass 1

m = mass 2

r = distance between the two bodies

Gravitational acceleration equation?

a = F/m = (GM)/r²

a = acceleration

F = force

m or M = mass

G = gravitational constant (6.67×10^-11 Nm²/kg²)

r = distance between bodies

Keplers first law of orbitals

Planets orbiting the sun travel in elipses with the sun as one of the foci.

Keplers second law of orbitals

A line that connects a planet to the sun sweeps out equal areas in equal time periods, giving spaces of equal area.

Keplers third law of orbitals

The square of the period of a planet’s orbit is prportional to the cube of its mean orbital radius.

What is the eqution for Keplers third law?

T²/R³ = (4pi²)/GM

T = the period

R = radius

G = gravitational constant (6.67×10^-11 Nm²/Kg²)

M = Mass

Explain Newton’s law of universal gravitiation.

Every particle in the universe attracts every other particle witha force along a line joining them. This force is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Gravitational field strength, define

The force per unit mass that would be exerted on a small mass at that point.

Coulomb’s law states that:

The magnitude of the electrostatic force of attraction or repulstion between two point charges is directly proportional to teh product of the magnitudes of charges and inversely proportional to the square of the distance between them.

Coulombs law equation

F = (kQq)/r²

F = force between the two objects

k = 9×10^9 (Coulombs constant)

Q = charge of object A

q = charge of object B

r = distance between the two objects centres

Define electric fields

the region of space surrounding a charged object in which other charged objects experience a force of attraction or repulsion.

How to calculate the electric field strength at one point

E = (kQ)/r²

E = electric field strength

Q = charge of the object

r = distance of the point from the object

In which direction do electric field vectors point?

Away from positive or towards negative.

How to calculate electric field strength

E = V/r

E = electric field strength

V = voltave of the battery supplying the current

r = distance between the plates

Define electric potential energy

the capacity for doing work which arises from position or configuration in an electric field.

Moving closer = increasing EPE

Moving away = Decreasing EPE

Electric potential equation

V = U/q

V = difference in voltage

U = difference in work done

q = charge of the object

also

qV=1/2mv²

Magnetic field in simple terms

A region of space around a magnetic material or moving electric charge in which the force of magnetism acts.

What happens when charges move through an insulated material?

A magnetic field is induced. Moving charges generate magnetic fields.

Right hand grip rule

thumb goes in the direction of the wire then fingers curl around in the direction in which the magnetic field flows.

equation for the magnitude of the magnetic field

B = (mu naught*current)/(2pir)

B = magnetic field strength

mu naught = 4pi*10^-7

r = perpendicular distance between the wire and the point

I = current of the wire

Solenoid right hand grip rule

Thumb points towards the direction of the magnetic north pole and the fingers wrap around in the direction of the current.

Solenoid magnetic field strength

B = mu naught*n*I

B = magnetic field strength

mu naught = 4pi*10^-7

n = number of turns/length of solenoid

I = curret flowing through the solenoid

Current carrying wire in a magnetic field equation

F = BILsin(theta)

F = force

B = magnetic field

I = current

L = length of wire

Theta = is the angle between the magnetic field and the wire

Magnetic force on a moving charge equation

F = qvBsintheta

F = force

q = magnitude of the charge

v = velocity of the charge

B = magnetic field

theta = angle charge is moving through

Right hand rule

Hand flat

Thumb = direction of current

Fingers = direction of magnetic field

Palm = direction of force on wire/particle

Describe magnetic flux

the amount of magnetic field strength that is passing through a specific area

magnetic flux equation

phi = BAcostheta

phi = magnetic flux

B = magnetic field

A = area

theta = angle between conductor and field

Electromagnetic induction

Moving magnetic fields produce a current and moving currents produce a magnetic field.

Faradays law equation

emf = -n*phi/t

emf = voltage induced in the conductor

n = number of turns in the conductor

phi/t = change in magnetic flux over time

Faradays law states

An emf is induced in a conductor whenever the magnetic flux linkage through the conductor changes. The magnitude of the induced emf in a conductor is directly proportional to the rate of change of magnetic flux linkage.

Lenz’s law states

the induced emf will always give rise to a current whose magnetic field opposes the direction of the original change in flux

How does Lenz’s law show that is obeys the law of conservation of energy?

The mechanical work is converted into electrical energy. In the absence of the magnet's movement, no mechanical work is done. Thus, no EMF is produced in the coil.

Transformer equations

I(p)V(p) = I(s)V(s)

V(p)/V(s) = n(p)/n(s) = I(s)/I(p)

I = current

V = voltage

n = number of coils

p = primary coil

s = secondary coil

Transformer basic definition and how does it work

a device that transfers electrical energy from one circuit to another. Transforming its initial electrical energy into a magnetic flux which is then transformed back into electrical energy in a new circuit. The two circuits contain a different number of loops and therefore, the voltage is also changed

What is the difference between step up and step down transformers?

Step up = primary to secondary coil (more coils in secondary than primary) giving an increase in voltage

Step down = primary to seconday coil (more coils in primary than secondary) giving a decrease in voltage

Explain how transformers work in terms fo Faradays law and electromagnetic induction

A change of magnetic flux through a conducting loop can induce an emf in the loop. Transformers contain a pair of windings, and they function by applying Faraday's law of induction. AC passes through the primary winding, which creates a varying magnetic flux. t induces a current in the secondary coil as par Faraday's Law. The magnetic field that results strikes the second winding and generates an AC voltage in that winding via electromagnetic induction.

Define elctromagnetic radiation

a kind of radiation including visible light, radio waves, gamma rays, and X-rays, in which electric and magnetic fields vary simultaneously

Describle how electromagnetic radiation is propogated by the interaction between electric and magnetic fields.

Oscillating charged particles induce a magnetic field. This subsequently induces an electric field perpendicular to the magnetic field.

What is the speed at which light moves through a vacuum?

3.00×10^8m/s

What speed is constant no matter how fast a frame of reference is moving?

The speed of light

What is the muon anomally?

Muons only have a lifetime of 2.2 microseconds at which point they decay into an electron of the same charge as the muon and two kinds of neutrino.

Muons are produced about 10km above the earth, according to newtonian physics with muons travelling at 0.9c would only be able to travel 660 m in their given lifetime. However there are still 50% detected at the earth level so how is this possible?

Special relativity explains that this is possible through different frames of reference.

The scientists frame of reference (observer) and the Muons frame of reference (inertial). From the scientists frame of reference the muon lives longer than its lifetime however the muon is moving at relativistic speeds causing the muons frame of reference to actually only be 2.2 micro seconds but the distance they travel being percieved as significantly shorter.

What is a rule that exhibts time dilation?

Moving clocks run slower

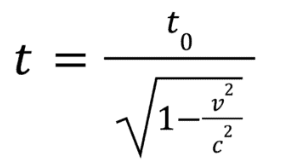
What is this?

Time dilation equation

What gives how long an event takes in the inertial frame of reference (the moving frame)?

Dilated time

What length of time does the observer (stationary frame of reference) experience?

True time

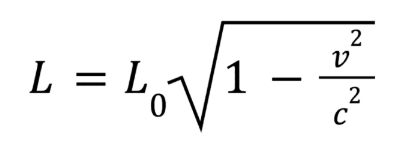
What is this?

Length contraction equation

Which frame of reference experiences Length contraction?

The observer

What length does the inertial frame of reference experience?

True length

Describe simultaneity

when two observers measure two events as happening at different points in time

A train paradox (lightning trees) what is experienced by a stationary observer?

The two trees are hit at the same time by lightning.

A train paradox (lightning trees) what is experienced by an inertial observer going at 0.8c?

The tree they are heading towards is hit first.

Explain train and flashlight paradox.

An observer is standing outside the train watching it go by at relativistic speeds, at the moment that the train has this person at the mid point, a person inside the train in the middle turns on their flashlight.

From the inertial frame of reference the light hits both sides of the train at once and the stationary observer is moving past them.

From the stationary frame of reference it is percieved that the light hits the front of the train first then the back of the train.

Explain the twins paradox. Frames of reference included

Imagine that there are two twins on Earth. One of the twins leaves Earth on a spaceship going at reletavistic speeds for some amount of time and then returns. When he returns he is noticeable much younger than the twin that stayed on Earth, how is this possible?

From the stationary twins perspective the time moves slower on the rocket therefore experiencing dilated time.

This paradox can be explained as a consequence of time dilation in special relativity. The Older twin experienced proper time and therefore more time than his younger twin.

Explain the Barn and ladder paradox

Theres a 20m ladder that you want to fit inside a 10m barn with both doors closed, doors will close once the ladder is fully in the barn.

Observer with the ladder starts moving at relativistic speeds thus the stationary observer experiences the ladder as shorter thus it can now fit in the barn however in the POV of the with lader observer the barn contracts so the ladder cannot fit in the barn.

Both perspectives are correct and the paradox arises by the misunderstanding of absolute simultaneity.

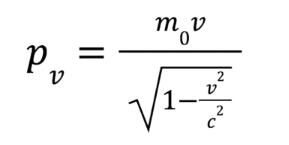
What is this?

Relativistic momentum equation

Mass energy equivalence

E = mc²

Define frame of reference

the stationary observers percieved reality, proper time with contracted length

Define the inertial frame of reference

The moving observers percieved reality, dilated time with proper length

Einsteins two postulates of special relativity

1. The laws of physics are the same in all inertial frames of reference.

2. The speed of light is constant for all frames of reference, no matter their motion or the motion of the light source.

Define rest mass and give equation for reletavistic mass

mass of an object measured in the same frame of reference as the object itself

reletavistic mass = lorenz factor * rest mass

Why can no object with mass travel at the speed of light in a vacuum?

Due to the infinate amount of energy required to propell mass to the speed of light

Explain Young’s double slit experiment. What model of light does it support?

You have two walls the front wall and the back wall. The front wall has two slits next to each other and a light is shone through both. One would assume the light passes through and leaves two lines on the back board but this is not the case. Instead there is a diffraction pattern on the back wall that shows where the wavelengths of light have constructively and desctructively superimposed. Constructive superposition is shown through the bright spots and destructive super position is shown through the dark spots. This experiment supports the wave model of light.

Describe light as an electromagnetic wave …

electromagnetic waves produced by an oscillating electric charge that radiate out at the speed of light are mutually perpendicular electric and magnetic fields.

Define black body radiation

A black body is a theoretical object that can perfectly absorb and emit radiation of any wavelength. When this object’s temperature is increased, it emits a spectrum of wavelengths, with each temperature giving its own characteristic curve.

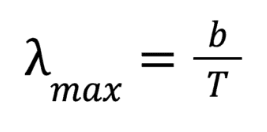
What’s this and what does it mean?

Black body radiation equation

Lambda = Wavelength

T = temperature of the body

b = wiens displacement constant (2.898×10^-3)

Black body radiation provides evidence of what?

Electromagnetic radiation is quantised into discrete values, packets or quanta.

Describe the concept of a photon

a minute energy packet of electromagnetic radiation

What is the photoelectric effect?

Where a light is shone on a material (e.g. metal) if the photon is at too low a frequency it will scatter, if the frequency of the photon is right or higher a photoelectron will be emitted.

Define threshold frequency

The minimum frequency of a photon, light or electromagnetic radiation required to cause the emission of photoelectrons or elecrtons from a metal surface.

What is Planck’s constant?

a fundamental universal constant that defines the quantum nature of energy and relates the energy of a photon to its frequency.

h = 6.626×10^-34

Define work function

the minimum quantity of energy required for an electron to be emitted from the surface of a metal plate.

Wave-particle duality exists in?

Photons and matter

Ultraviolet Catastrophy

at high temperatures there will be very low wavelengths produced such as UV and even gamma rays. This caused a great issue in physics at the time as it was found that more low wavelength particles were supposed to be produced than the energy used to make them thereby violating the conservation of energy.

Energy quanta of atoms

E = hf

E = energy

h = plancks constant (6.626×10^-34)

f = frequency

Combine formulas for wavelength and energy quanta of atoms

E = (hv)/lambda

E = energy

h = Plancks constant (6.626×10^-34)

v/lambda = frequency, v = velocity, lambda = wavelength

Kinetic energy formulas all equivalent values

Ek = hf - W = hf - hfo = qVc = ½ mv²

Describe Rutherford’s model of the atom

an atom with a small, dense nucleus surrounded by electrons.

Limitations of Rutherfords model of an atom

fails to explain the stability of the electrons orbital motion

It does not explain the spectrum of hydrogen and other atoms.

How does Bohrs model of the atom adress the limitations in Rutherfords model?

Bohrs model addressed the unaddressed instability of the Rutherford model by explaining the quantised nature of these orbits and how electrons within the same orbit posses the same discrete quantity of energy.

Bohrs atomic model

a small positive nucleus surrounded by negative electrons in set orbits of fixed energy.