section 4.1 Vector spaces and subspaces definitions and proofs

A ___ is a set of objects, called vectors, along with addition and scalar multiplication.

vector space, V

1st axiom: closed under addition - if u and v are vectors in V, then ___ must also be a vector in V

if u and v are vectors in V, then u+v must also be a vector in V.

axiom 2: commutativity of addition - u + v = ?

u + v = v + w

axiom 3: associativity of addition - (u+v) + w =?

(u+v) + w = u + (v + w)

axiom 4: zero vector - there exists a vector such that v + ? = v

there exists a vector such that v + 0 = v for all vectors in V

axiom 5: additive inverse - for every vector in V, there exists a -v such that v + ? = 0

for every vector in V, there exists a -v in v such that v+(-v) = 0

axiom 6: closed under scalar multiplication - if v exists in __ and c exists in __, then __ must also exist in V.

if v exists in V and c exists in R, then cv must also exist in V.

axiom 7: multiplicative identity :1v = ? for all vectors in __

1v = 0 for all vectors in V.

axiom 8: associativity of scalar multiplication : c(dv)=?

c(dv) = (cd)v

axiom 9: distributive law over vector addition: c( u + v) = ?

c( u + v) = cu +cv

axiom 10: distributive law over scalar addition: ( c + d)v =?

(c + d)v = cv + dv

prove that the zero vector is unique

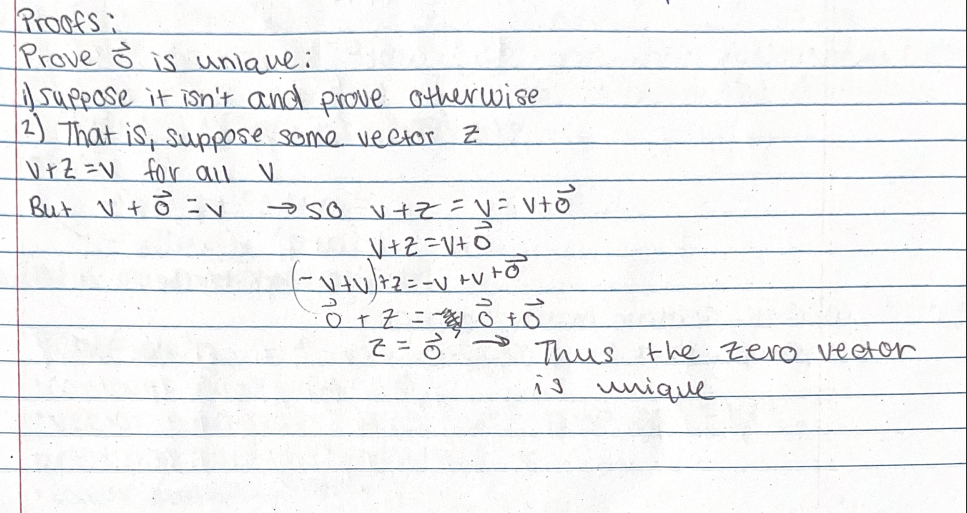
Prove that for every 𝑣∈𝑉 ( vector v in V), the additive inverse −𝑣 is unique.

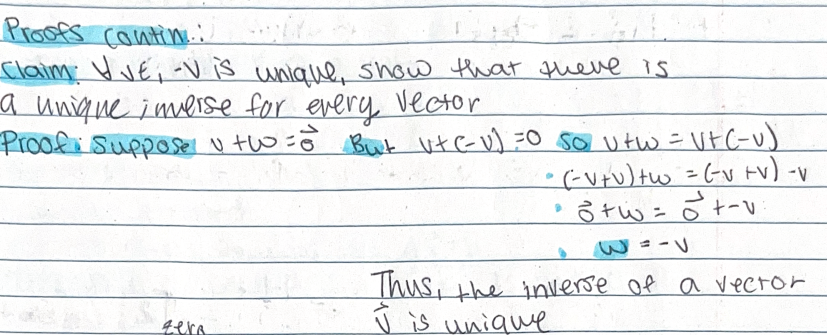
Prove that 0𝑣=0 for any 𝑣∈𝑉 (v in V).

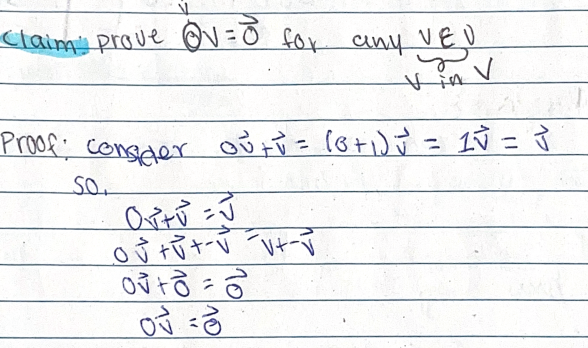
Prove that (−1)𝑣=−𝑣 for any 𝑣∈𝑉.

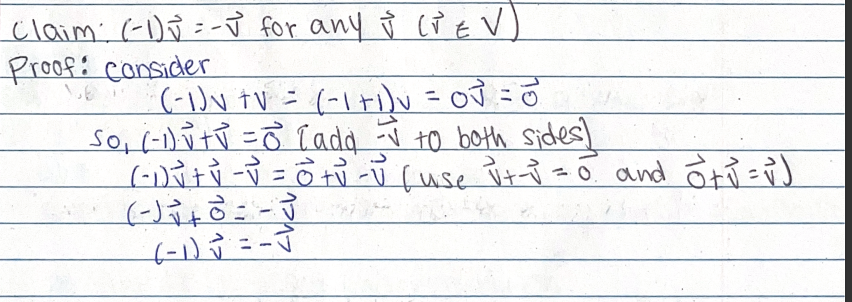
Subspace: A subspace H of V is a subset for V which is also a ___

vector space

H is a subset of V if?

1) The zero vector is in the subset

2) H is closed under scalar multiplication 3) H is closed under addition

Span: the span of x amount of vector is the set of _____

all linear combinations

If u and v are in V, why is u + v in V?

because both of its entries will be nonnegative

Determine if the following set is a subspace of P_n

All polynomials of the form p(t)=at², where a is in ℝ.

T

“ “ All polynomials of the form p(t)=a+t², where a is in ℝ.

T

“ “ All polynomials of degree at most 3, with integers as coefficients.

F

“ “ All polynomials in ℙn such that p(0)=0.

true