Maths Matrices

Linear System with No Solution

• This is inconsistent

• Means there is no solution

• The three planes never cross

Linear System With Non-Unique Solution

• This is consistent

• Means there are multiple solutions

• The three planes cross along a line

Linear System With No Solution

• This is inconsistent

• Means there is no solution

• The three planes never cross

Echelon Form

In a row with x y and z

Ax = b Form

is a representation of a linear system where A is a coefficient matrix, x is a vector of variables, and b is a constant vector, used to find solutions to linear equations.

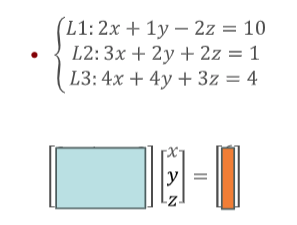
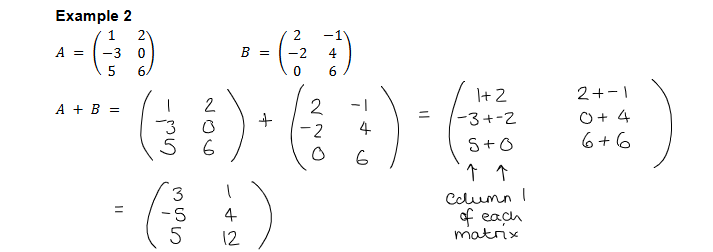
Adding And Subtracting Vectors

• Basically just add the same rows and columns together

Matrix Multiplication

• Go along the first row and down the first column

• Can only multiply A and B only if number of columns in A = number of rows in B

Determinants (2 × 2)

Det (a b ¬ c d) = ad - bc

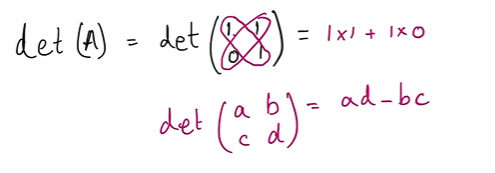
Determinant (3 × 3)

For higher order matrices the determinant is calculated as seen with the vector
product.

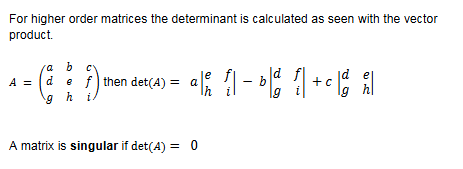
Transpose Matrix

A transpose matrix 𝐴𝑇 is the created by swapping the rows with the corresponding
columns of the matrix 𝐴

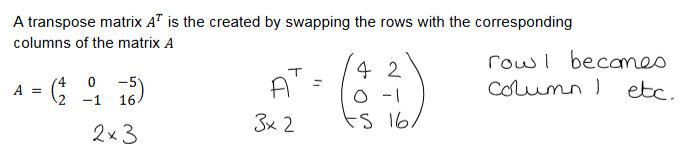
Identity Matrix

An identity matrix is a diagonal matrix with all its main diagonal entries as one. Note that by definition an identity matrix is always square. The identity matrix is often denoted by 𝐼 or 𝐼𝑛

• Multiplying by an identity matrix does not change anything

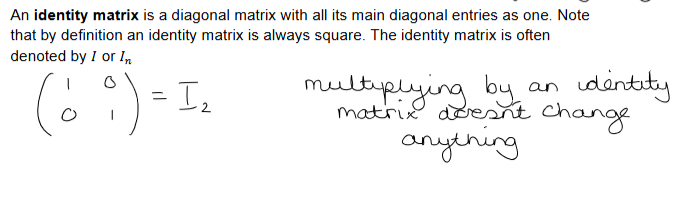
Inverse Matrix (2 × 2)

Given a matrix 𝐴 if there exists a matrix 𝐵 such that 𝐴𝐵 = 𝐵𝐴 = 𝐼 then matrix 𝐵 is
said to be an inverse matrix of 𝐴. We denote an inverse matrix by 𝐴−1 rather than a different letter.

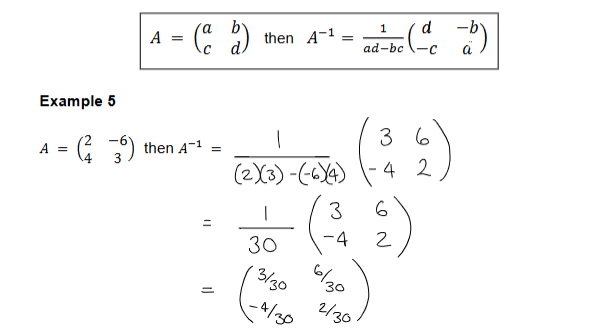
Inverse Matrix (3 × 3)

Suppose we have a square matrix 𝐴 we wish to find the inverse of. We can do this
by first augmenting 𝐴 with the equivalent size identity matrix to give (𝐴|𝐼). Next, we
perform row operations to the whole of this augmented matrix until the left hand side becomes the identity and the resulting matrix on the right will be the inverse.

Determinant (3 × 3) Laplace’s Expansion

Inverse Via Adjugate Method

LU Decomposition

A method of factorizing a matrix into the product of a lower triangular matrix and an upper triangular matrix, used to simplify solving linear equations or finding inverses.

A = LU

LUx = b