Math Torture

A subgroup H of a group G is called a ______, written H < G, if _____ for every a eG

normal subgroup of G, aH = Ha

Prove the Normal Subgroup Test

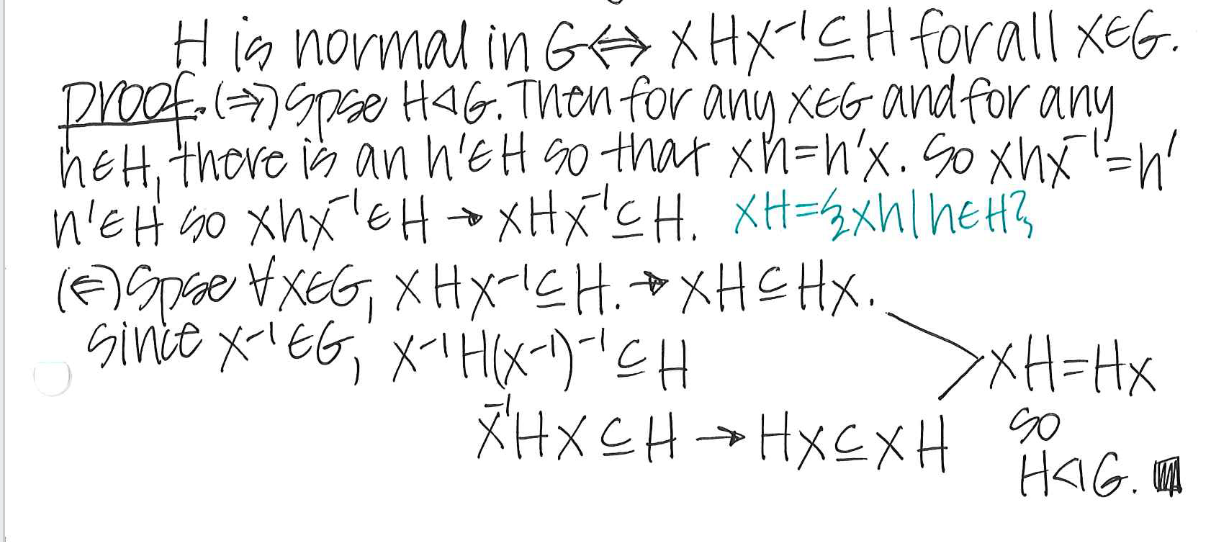
What is the Normal Subgroup Test?

H is normal in G if and only if xHx^-1 is an element for all x eG

If H is a subgroup of H, we can form the

factor group G/H “G mod H”

What is the G/Z Theorem?

If G/Z(G) is cyclic, then G is abelian.

Prove the G/Z Theorm

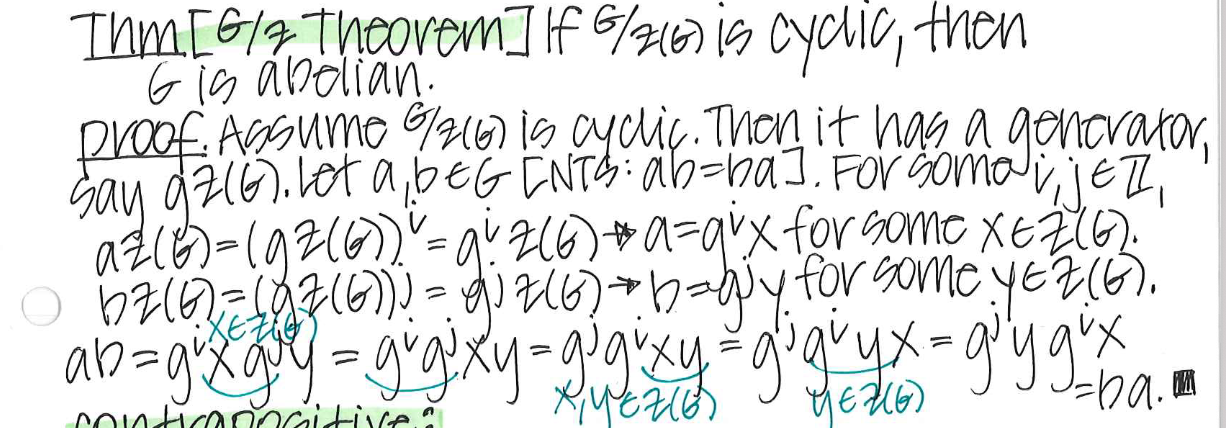
G is the _______ internal direct product of H and K, written G = H x K, if

internal direct product, H is a subgroup of G, K is a subgroup of G, the intersection of H and K is the identity, G = HK if HK is the {hk| h e H, k e K}

Theorem: H x K is isomorphic to ______

the external direct product of H and K

Of G is a group of order p² where p is prime, then

G is isomorphic or Zp² or G is isomorphic to the external direct product of Z_p and Z_p

A _____ from group G to group G’ is a map that is operation preserving. read:

homomorphism, so O (ab) = O (a) O (b)

The _____ is everything in the domain in the domain that get mapped to the identity of the codomain.

kernel of a homomorphism; so ker(o/) = {x eG| o/ = e}

IR[X]

group of all polynomials with real # coefficients, under addition

3 Properties of Homomorphism

Theorem: Suppose O/: G to G’ is a group homomorphism. Then the kernel is a subgroup G. Prove using the 2-Step Subgroup Test.

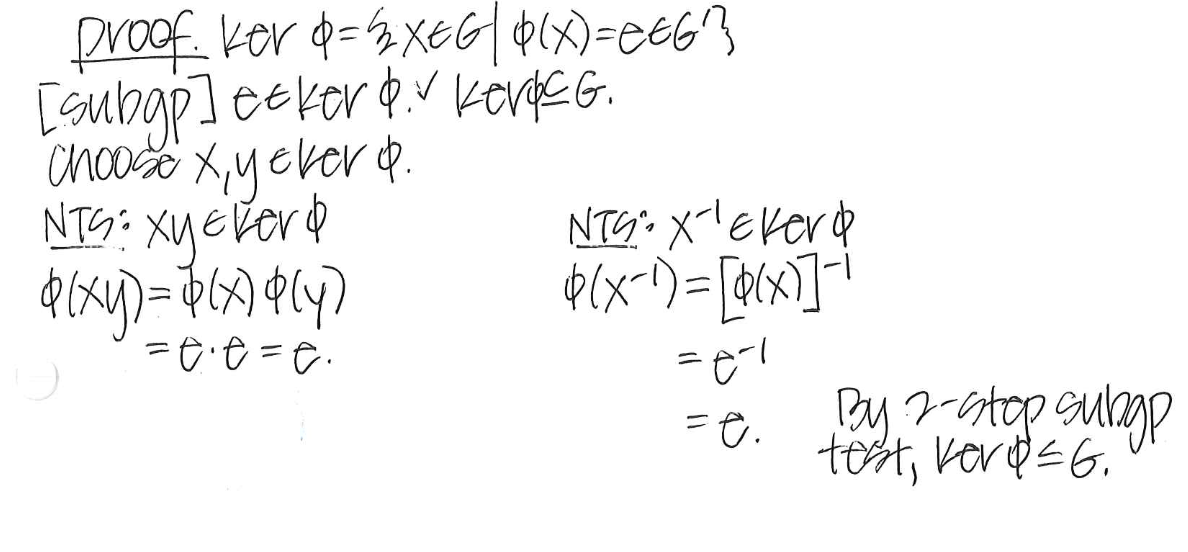
Theorem: Suppose O/: G to G’ is a group homomorphism. Then the kernel is a subgroup G. Prove using the Normal Subgroup Testx

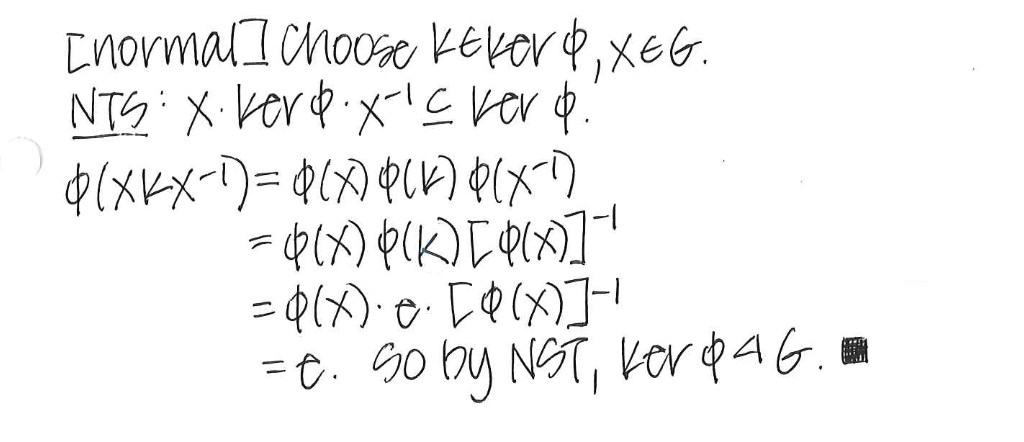
What is the Theorem FTGH? Suppose O: G to G’ is a group homomorphism. Then….

G/ker O is isomorphic to O(G)

What is the Fundamental Theorem of Finite Abelian Groups

What is a Ring?

A ring is a set R with two binary operations addition(a+b) and multiplication(ab)

A ring is a set R with two binary operations addition(a+b) and multiplication(ab) such that for every a, b, c e R…

If ab = ba, then R is ….

commutative

If R has a 1, then R is a

ring with identity/ ring with unity

If R is a ring with unity, then any element a for which a^-1 exists is called a

unit

Thm. [Multiplication Rules} Name three. Assume a, b, c e R

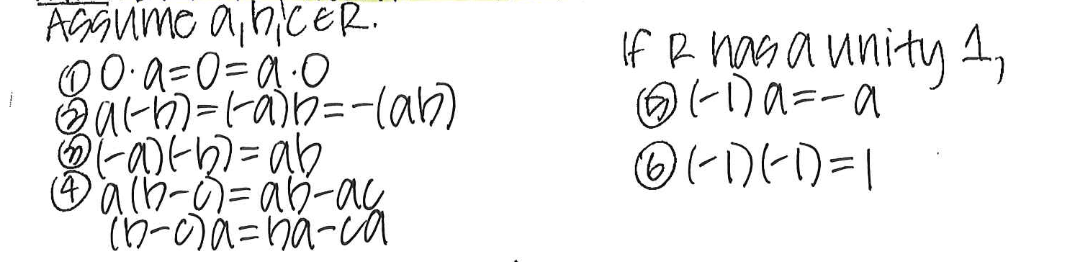
Thm. If R has a unity, it is _____. If a e R is a unity, then a^-1 , then a^-1 is ____.

Unique… unique

Let R be a ring, and let S be a _____ of R. Then S is a ____ of R if S is itself a ring under the same operation as R.

subset, substring

Prove the Subring Test

State the Subring Test

Let S be a nonempty subset of R. Then S is a subring of R, if, for every a,beS, both a-beS and abeS

What is a zero-divisor?

Non zero element a of a commutative ring R such that there is a nonzero element beR where ab=0

A______ is a Non zero element a of a commutative ring R such that there is a nonzero element beR where ab=0

zero-divisor

An integral domain is a commutative ring with unity that has no______.

zero divisors

An _____is a commutative ring with unity that has no zero divisors.

intergral domain

Z_p is an integral domain

State the Lemma

An _____ is a commutative ring with unity where the cancellation property holds.

integral domain

An integral domain is a commutative ring with unity where the ——— holds.

cancellation property

A ___ field is a commutative ring with unity in which every nonzero element is a unity.

Field.

Every field is an _____, since ab= 0 and a=/0 then a^-1 ab= a^-10

integral domain

Prove every finite integral domain is a field.

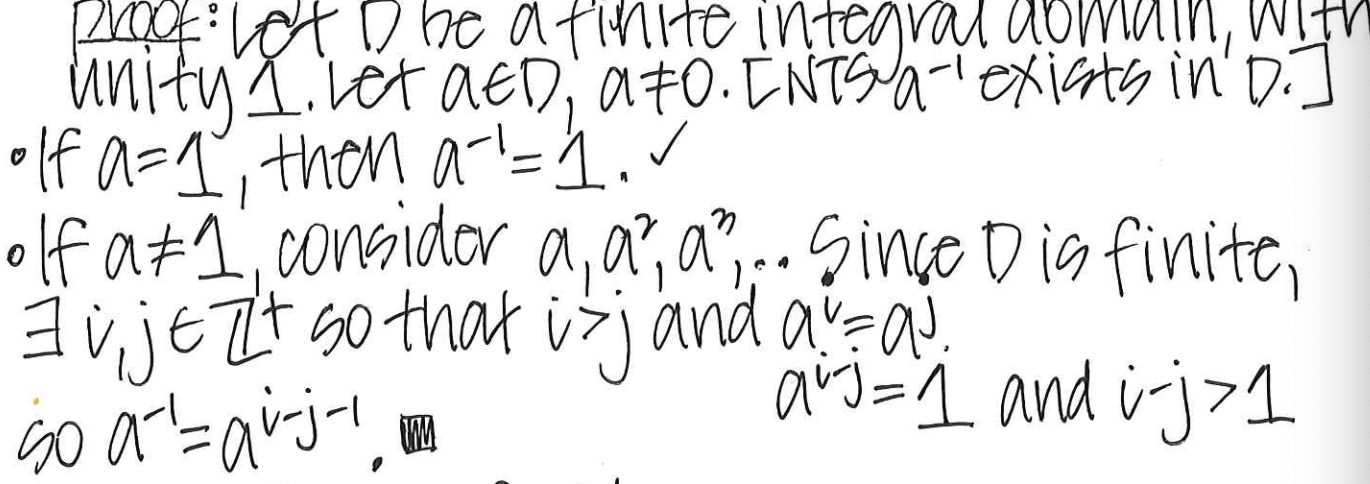
The ____ of a ring is the least positive integer n so that nx = 0, for all x eR.

characteristic

Thm. If a ring with unity 1, char(R) is the order of 1 under addition. Prove it.

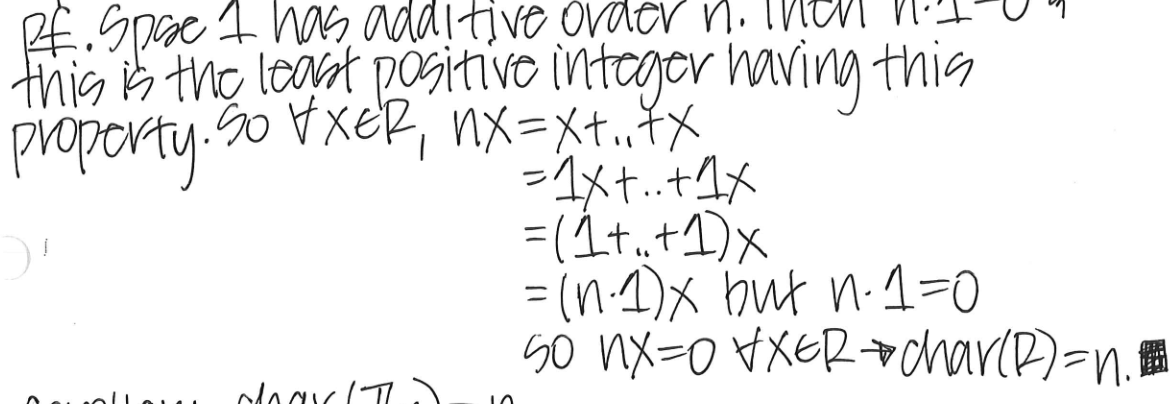
char(Z_n) =

n

Prove the theorem. The characteristic of an integral domain D is either zero or prime

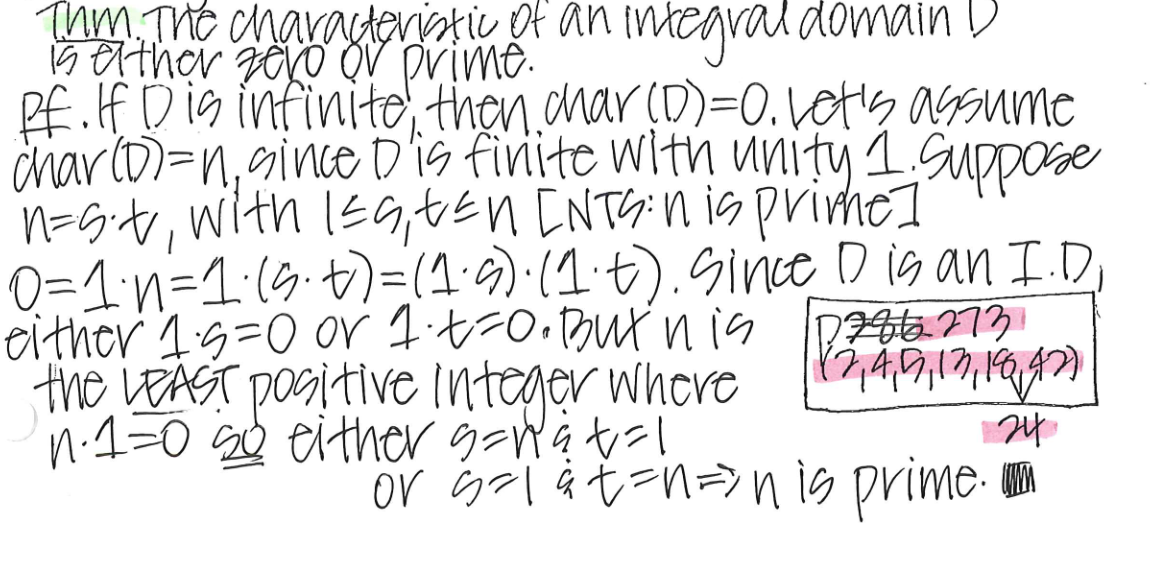
[Subring Test] Let S be a ____ ____ of ring R. If, for every a,b e S, both ____ and ____ then S is a subsring of R.

nonempty subset, a-beS and abeS.

Let A be a subring of R. Then A is a ______ ____ of R if for every reR, a e A, both ___ and ___.

(two sided) ideal, ra eA and ar eA

What is the ideal test?

Principal ideal generated by a is

generated by one element

Let R be a ring with ideal A.. The ___________ with operations (S+A)= + (t+A) = (s+t)+A and (S+A) (t+A) = (S*T) + A

factor ring R/A = {r +a|reR}

What is a maximal ideal of R?

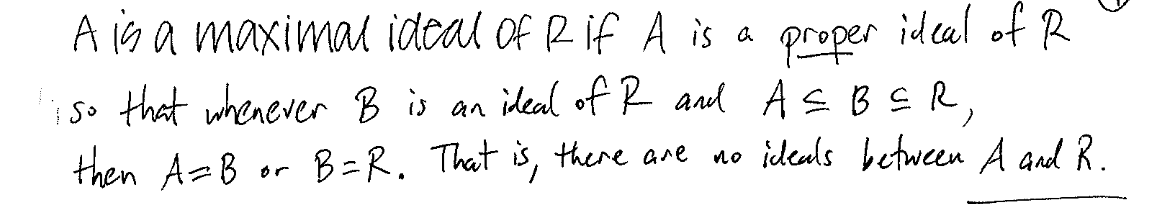
Theorem. A is a maximal idea of A if and only if

R/A is a field.

Ring Homomorphism

If O is a bijection, then O is a

ring isomorphism

Name three properties of Ring Homomorphisms

A _____ O:R to S is a mapping that preserves the two ring operations. So for all a,b eR, O(a+b) = O(a) +O(b) and O(ab) = O(a)*O(b)

If O is a bijection then O is a ______

ring homomorphism

ring isomorphism

Name three properties of ring homomorphisms