Unit 3 Geometry Terms

Interior Angles

The angles inside a polygon

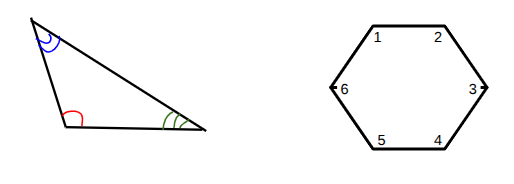
Exterior Angles

Formed by a side of a polygon and the extension of its adjacent side

***an exterior angle and its adjacent interior angle add to 180°

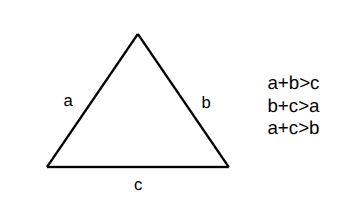
Triangle Inequality Theorem

The sum of the lengths of any two sides in a triangle MUST be greater than the third

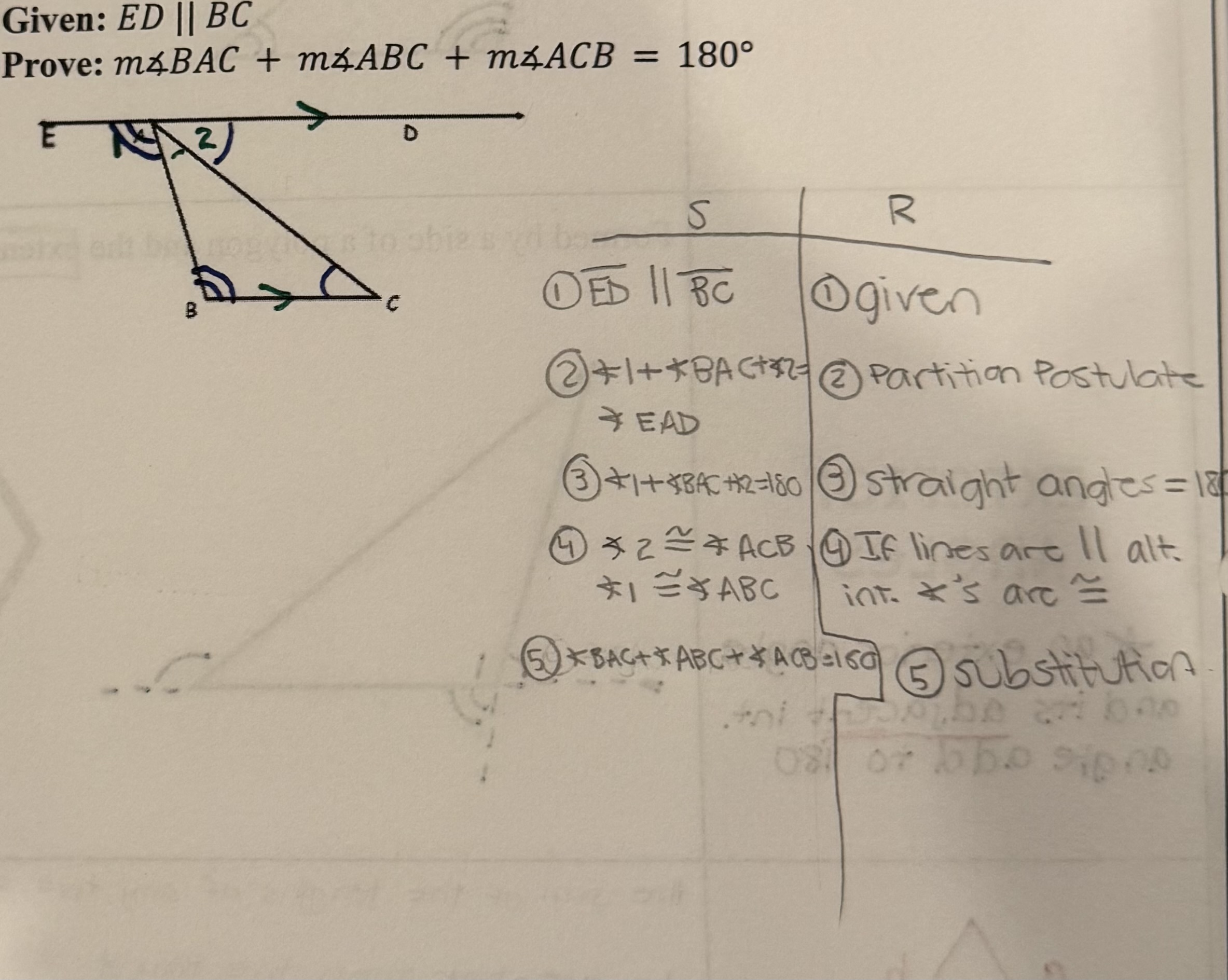
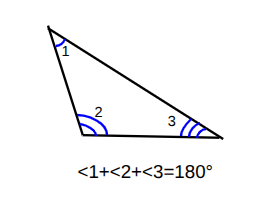
Triangle Angle Sum Theorem

the angles inside a triangle add to 180°

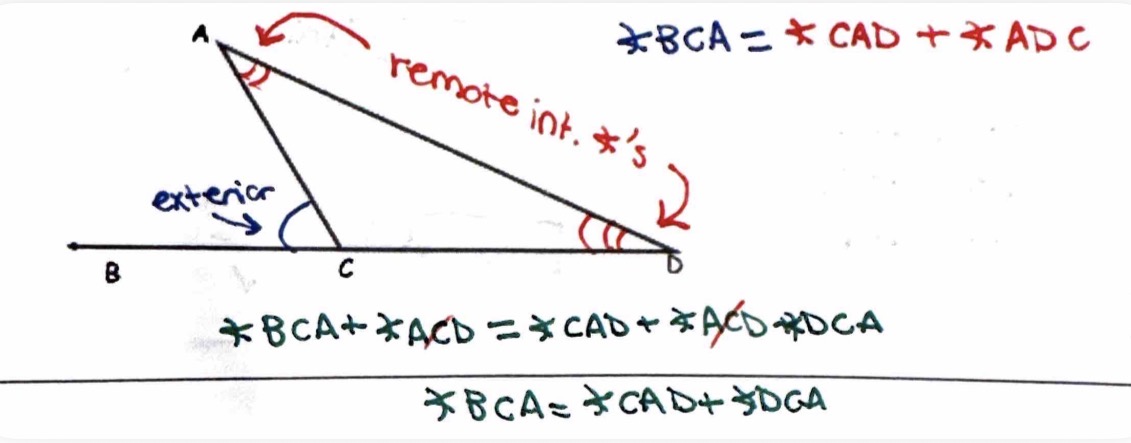
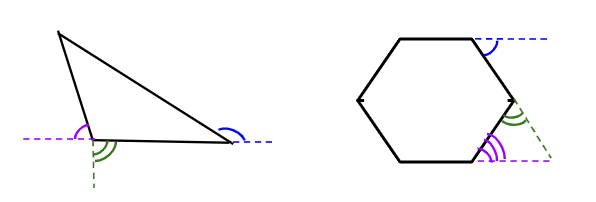
Exterior Angle Theorem

the exterior angle is equal to the sum of the remote interior angles

Scalene Triangle

has NO congruent sides or angles

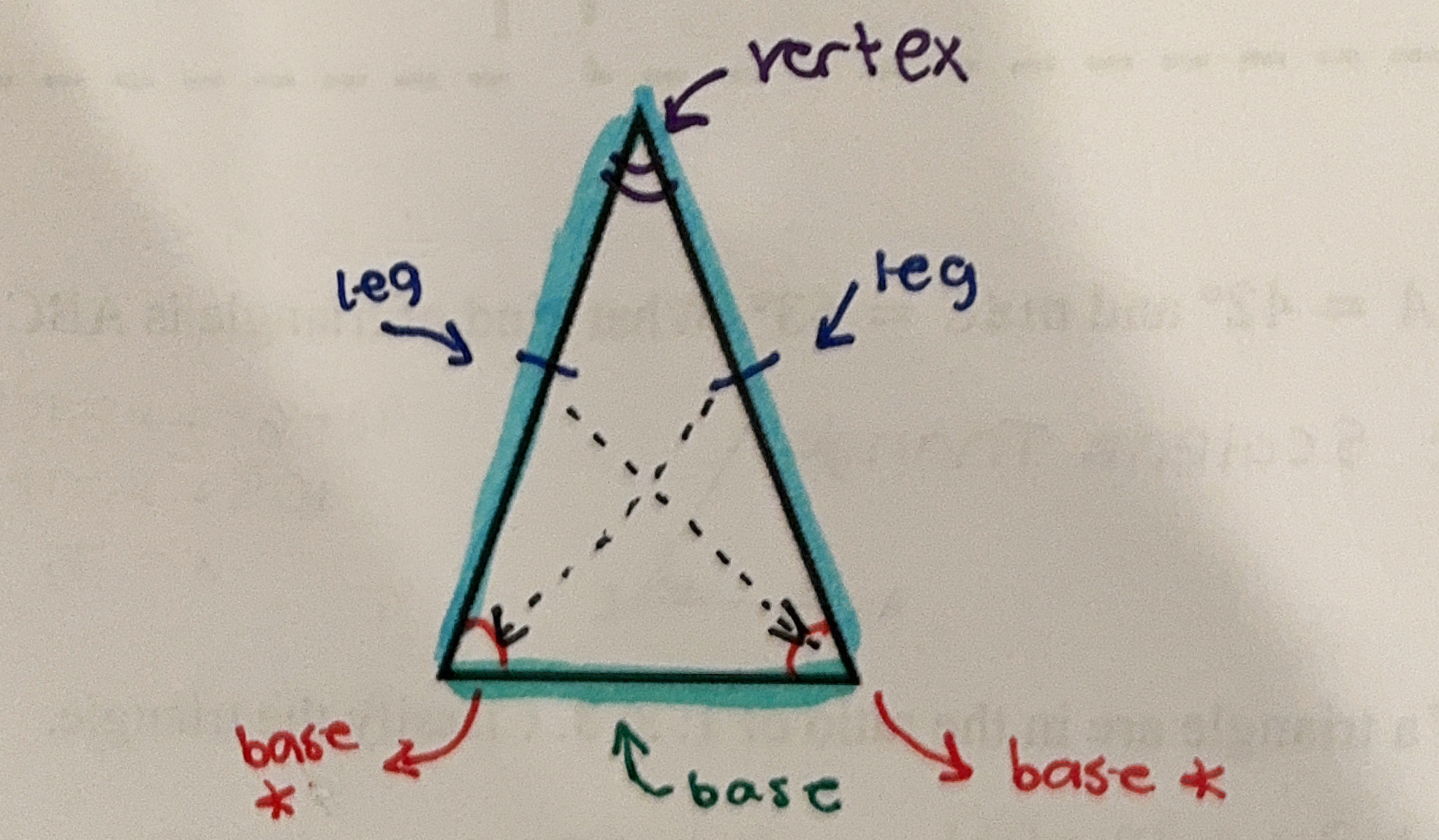
Isosceles Triangle

has TWO congruent sides and TWO congruent angles

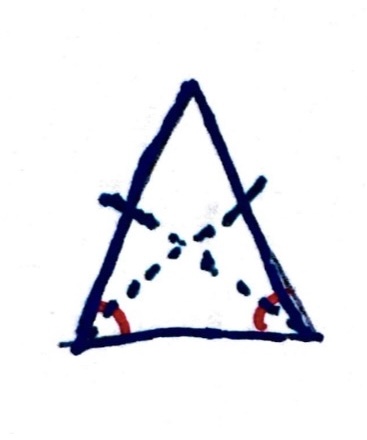
Equilateral Triangle

has THREE congruent sides and THREE congruent angles

***each angle is 60°***

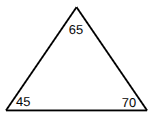
Acute Triangle

has ALL angles measuring less than 90°

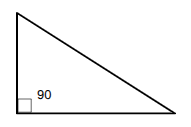
Right Triangle

has ONE right angle

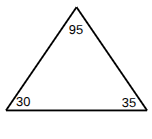
Obtuse Triangle

has one angle measuring greater than 90°

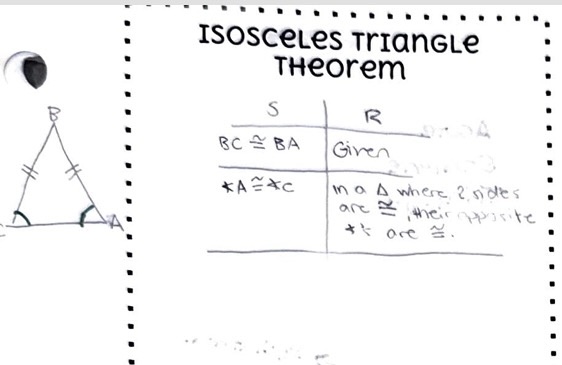
Isosceles Triangle Theorem

If two sides of a triangle are congruent, then the angles opposite those are also congruent

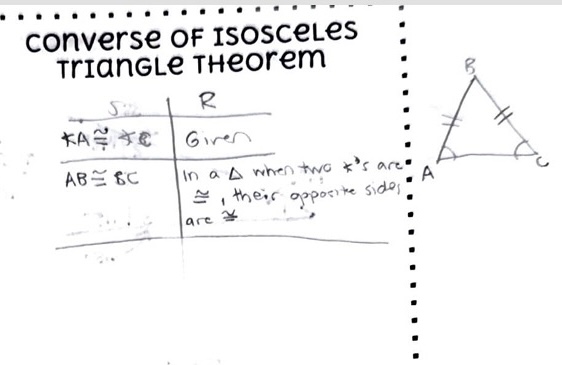
Converse of Isosceles Triangle Theorem

If two angles of a triangle are congruent, then the side opposite those are congruent

Midpoint

A point on a segment that creates two congruent pieces

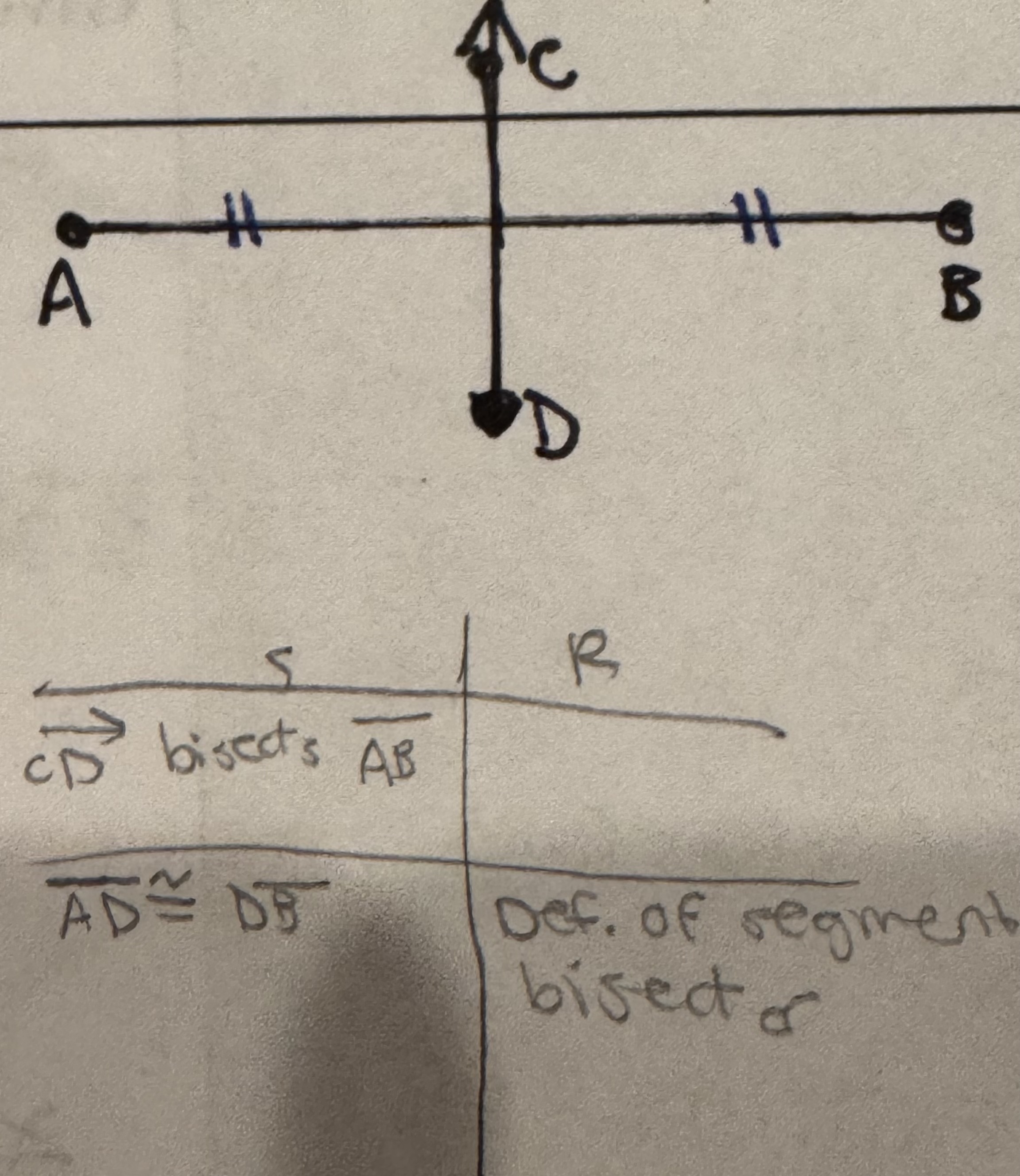
Segment Bisector

A line segment or ray, that splits a segment into two congruent pieces at the midpoint (mdpt.)

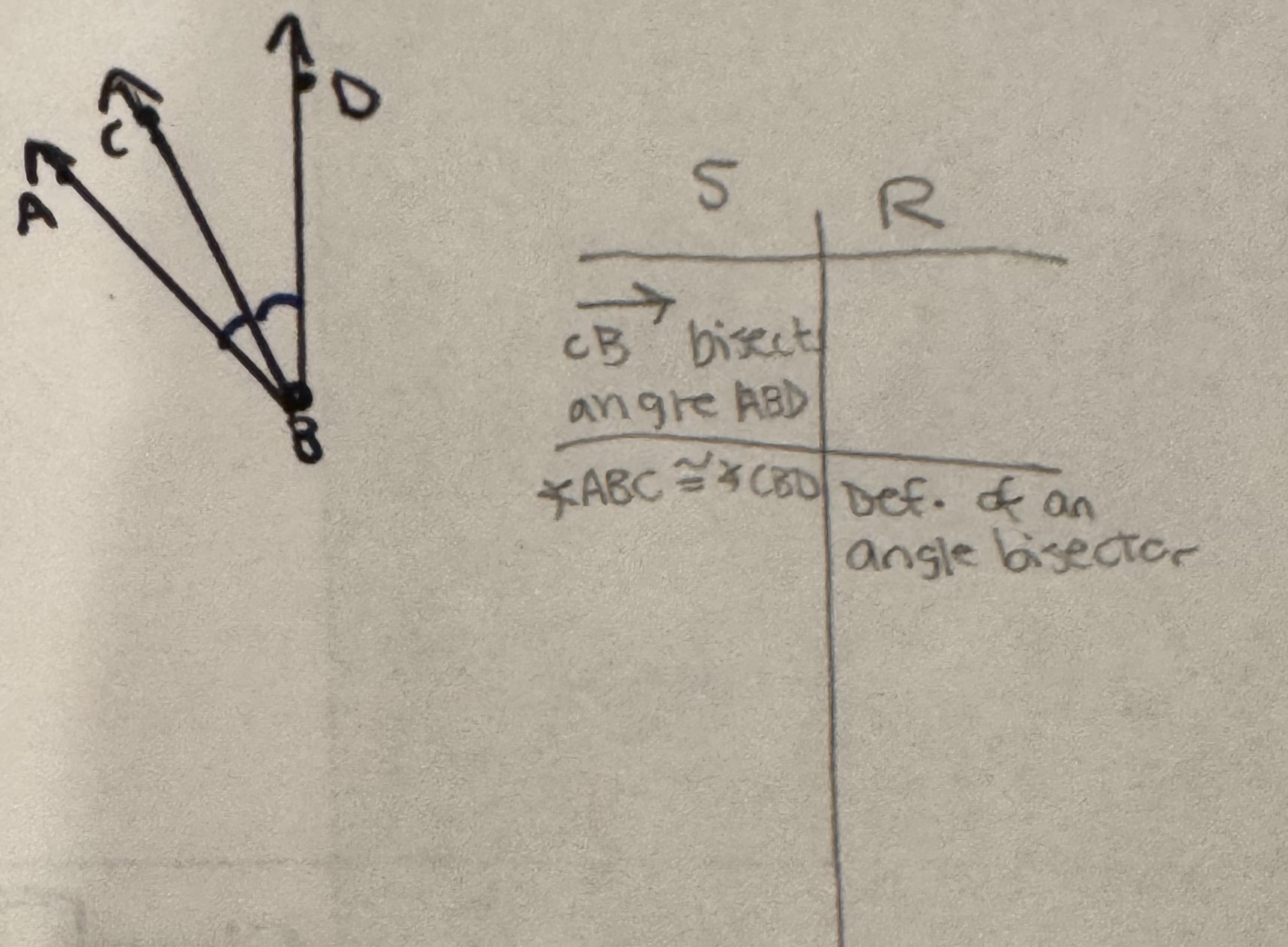
Angle Bisector

A ray that cuts an angle into two smaller congruent angles

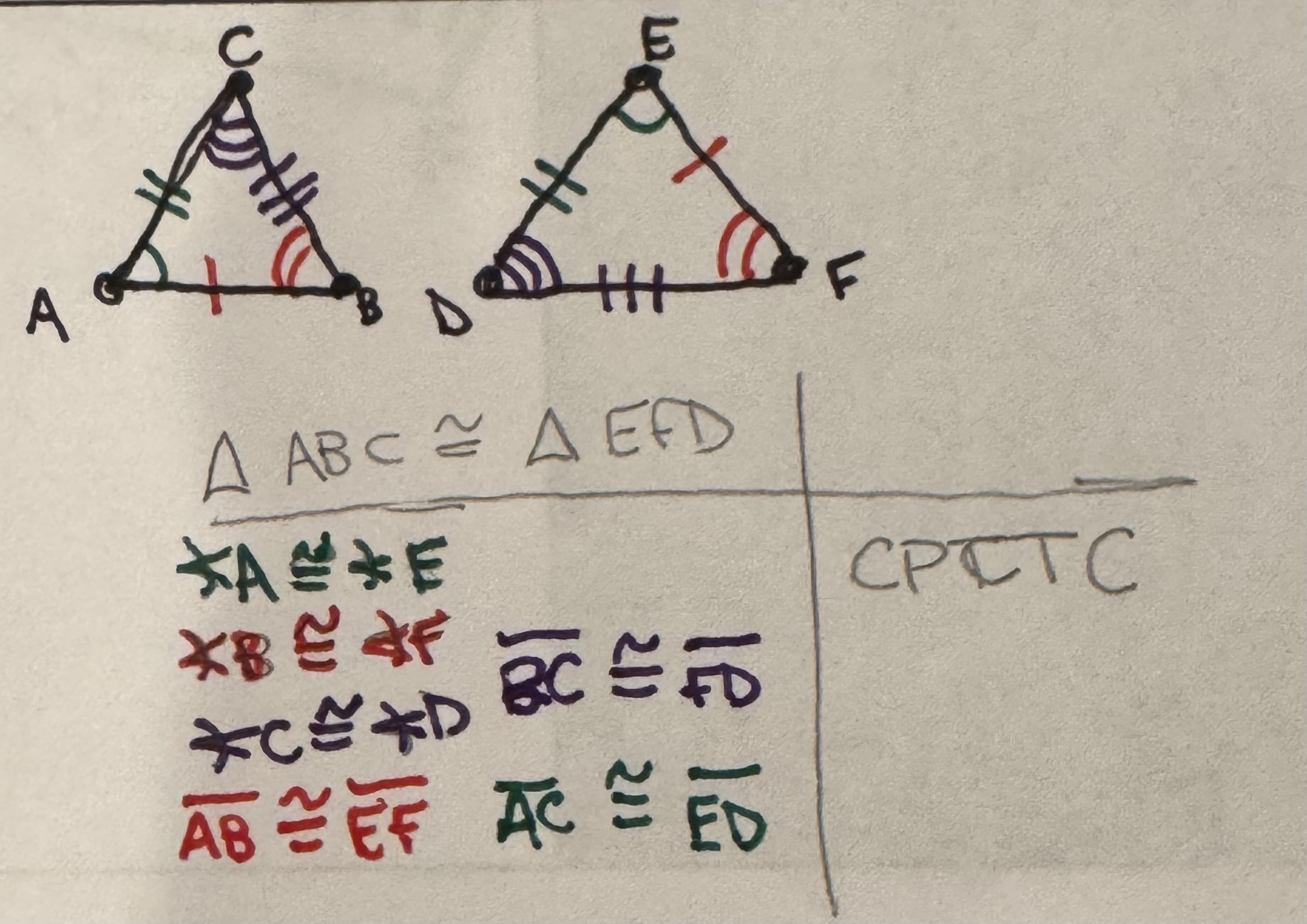
Corresponding Parts of Congruent Triangles (Polygons) Congruent (CPCTC)

in any two congruent polygons, corresponding angles and sides are congruent

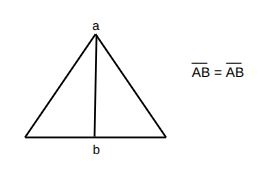
Reflexive Property

Any quantity is equal to itself

Ex: a = a, AB = AB

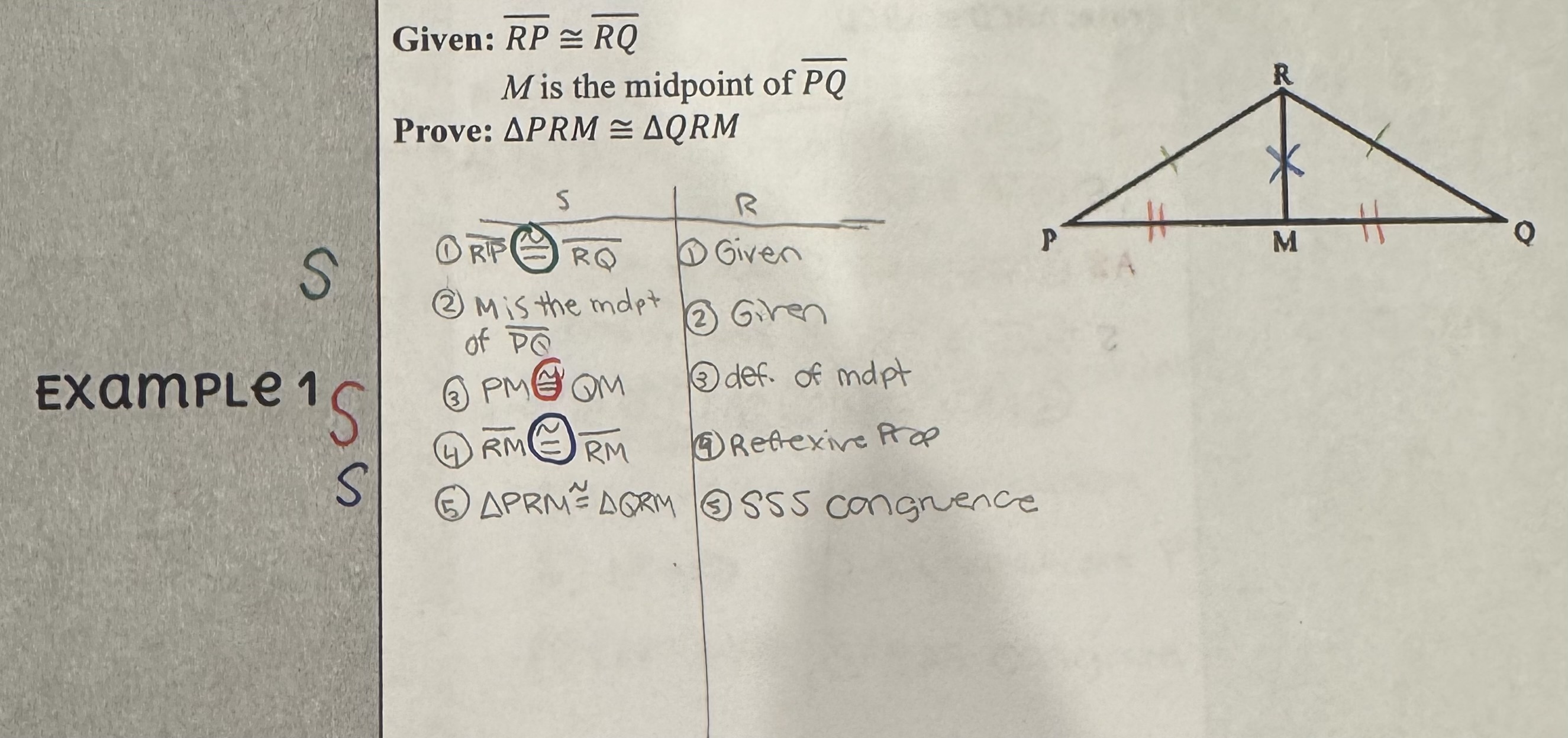
Side-Side-Side Congruence Postulate (SSS)

If three sides of a triangle are congruent to three sides of another triangle, this is enough info to say the triangles are congruent

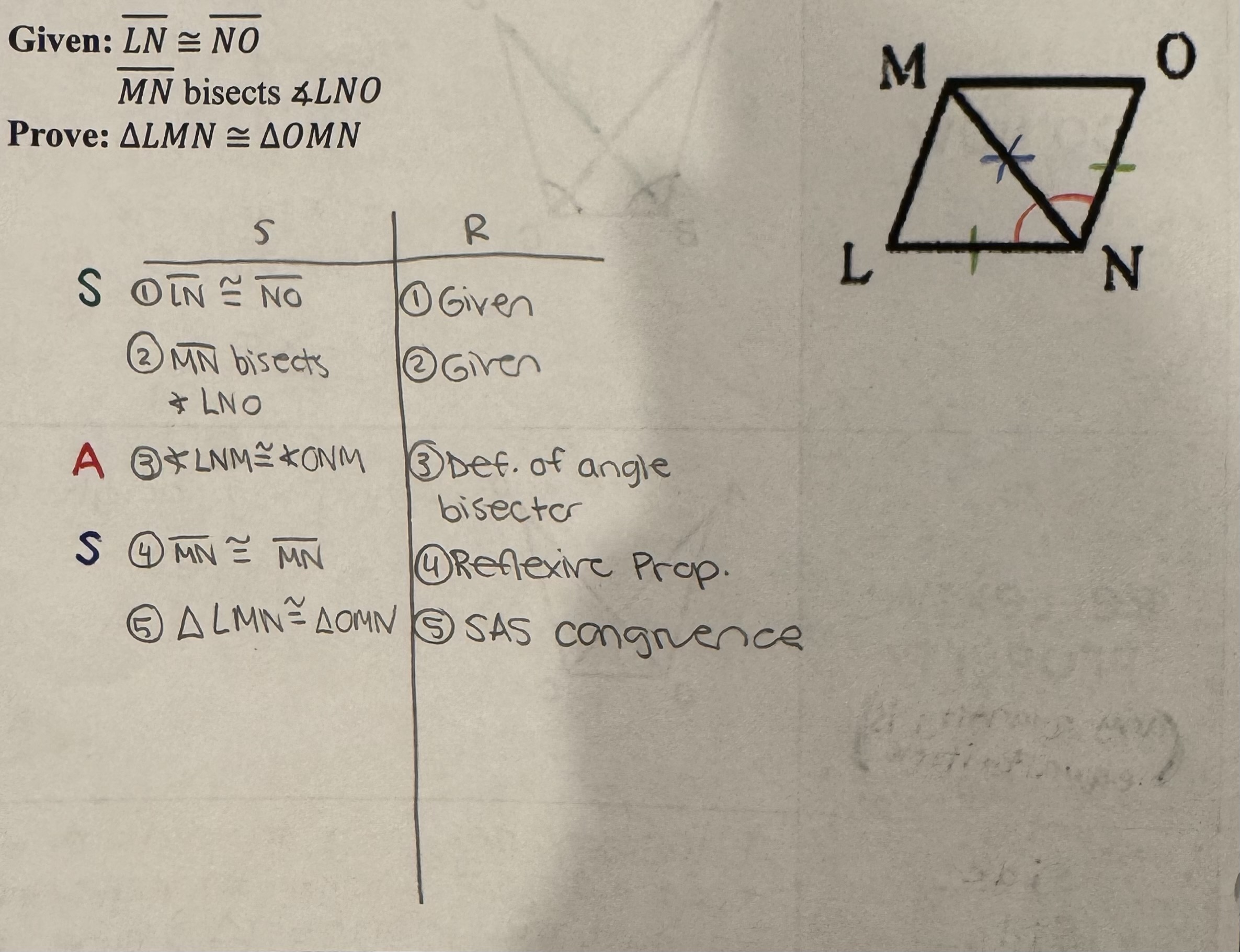
Side-Angle-Side Congruence Postulate

If two sides in a triangle and the included angle are congruent to two sides in the included angle of another triangle, that is enough info to prove triangles congruent

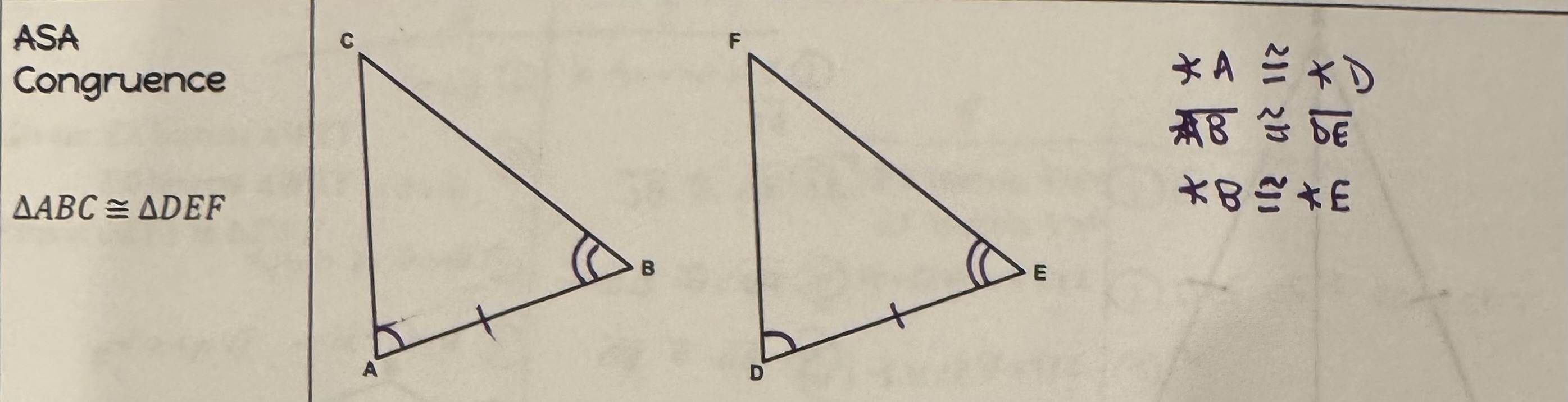
Angle-Side-Angle Congruence Postulate

If two angles and the included side of a triangle are congruent to the corresponding parts of another triangle, we can prove triangles congruent

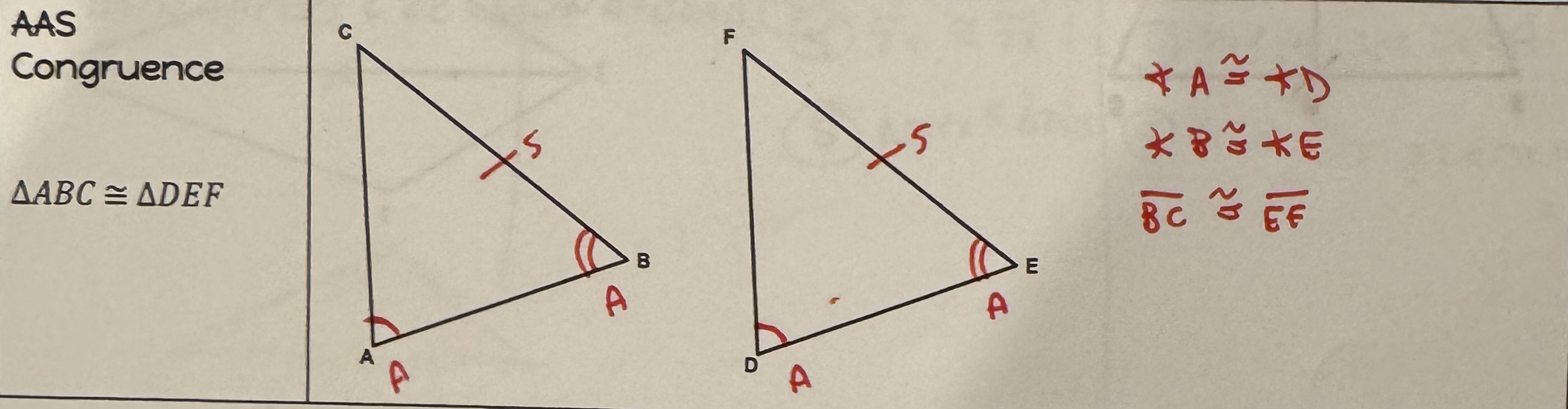
Angle-Angle-Side Congruence Postulate

If two angles and non-included side of a triangle are congruent to the corresponding parts of another triangle, we can prove triangles congruent

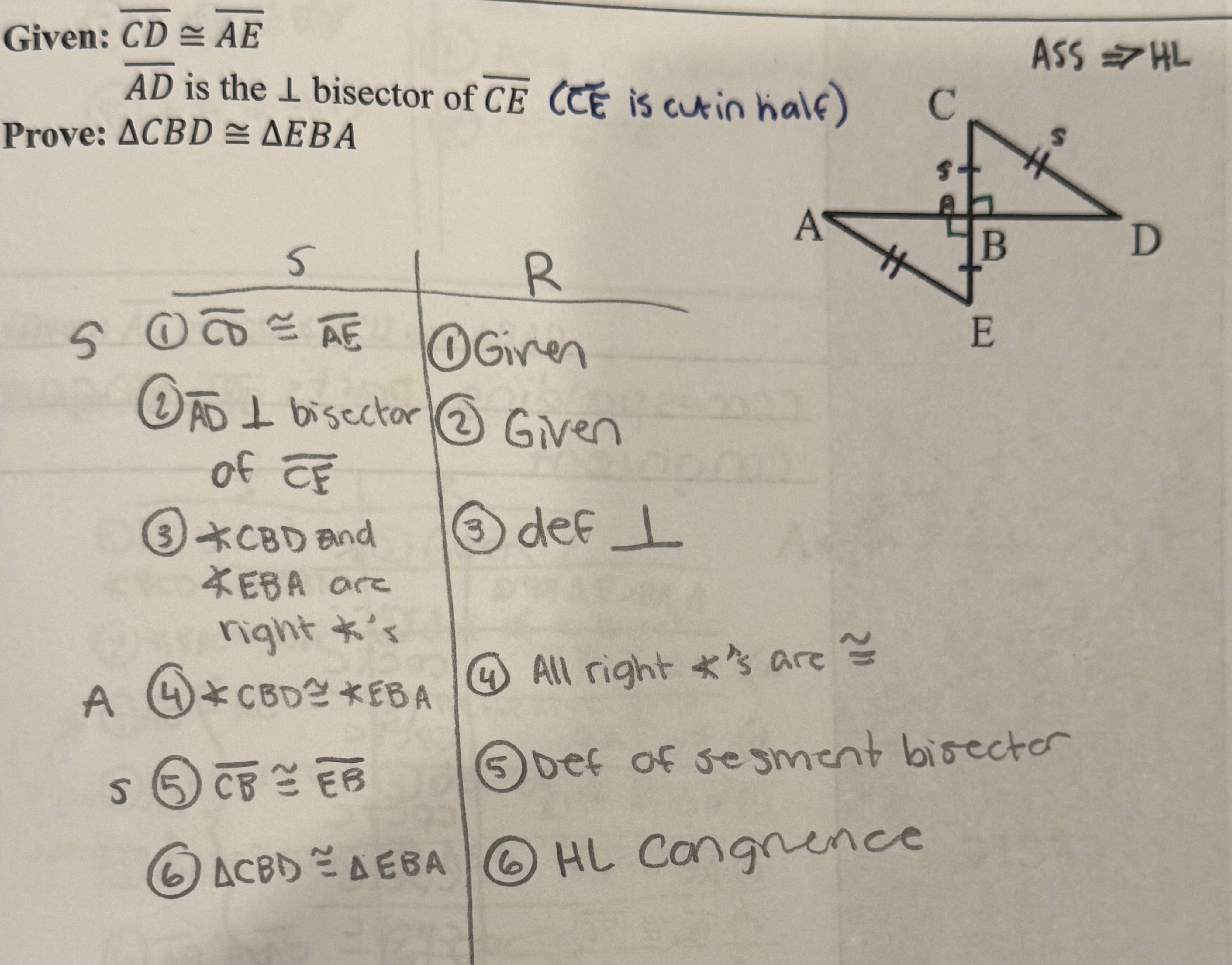
Hypotenuse Leg Congruence Postulate

If a triangle is right and it’s hypotenuse and a leg are congruent to another right triangle’s hypotenuse and leg then the triangles are congruent

***To prove triangles are congruent, we must show:***

1. right angles in each triangle

2. set of hypotenuse congruent

3. Set of legs congruent

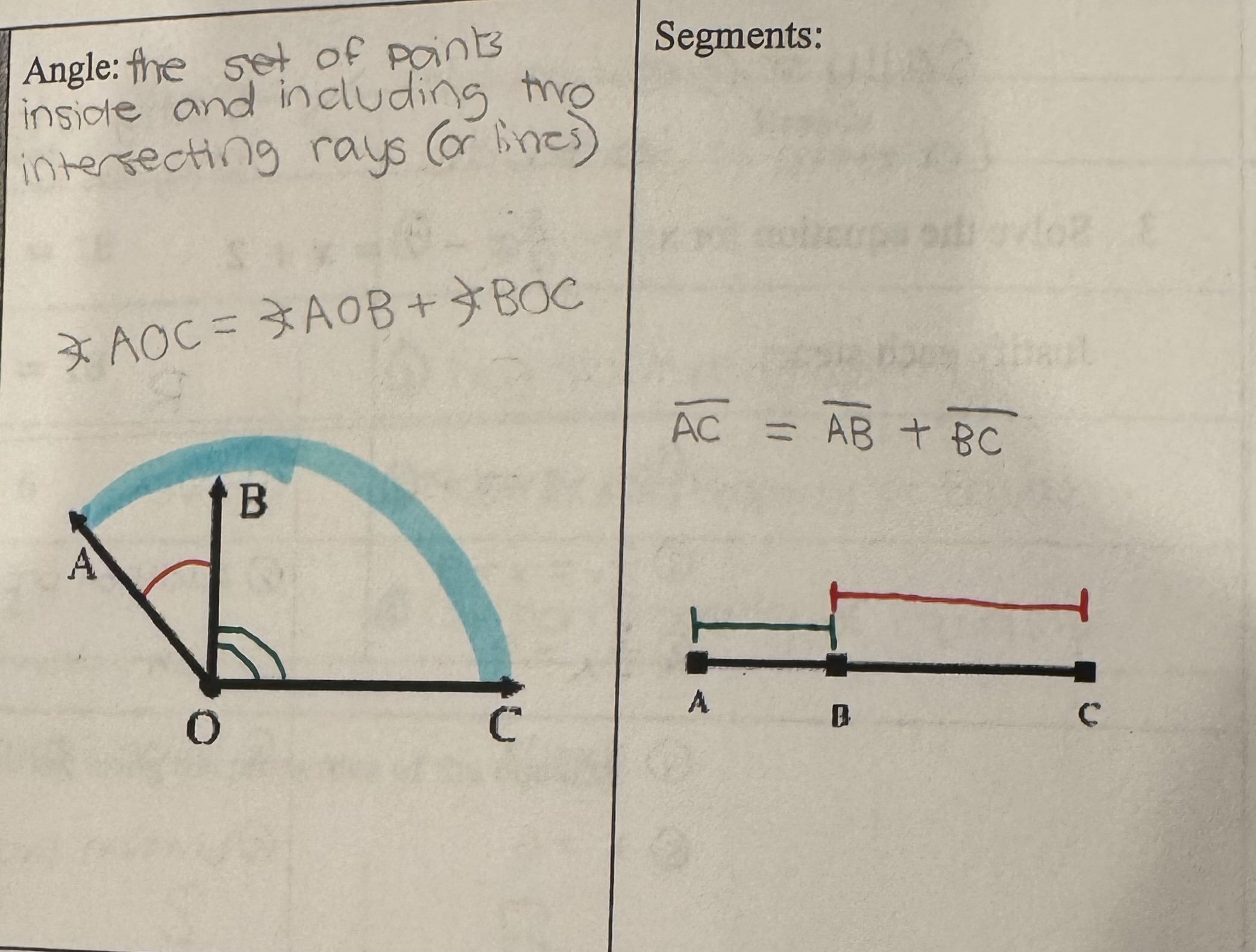
Partition Property (Partition Postulate)

A quantity is equal to the sum of its parts

Ex: <AOC = <AOB + <BOC