2.4 Electrostatics

What is the assumption of Barré de Saint Venant ?

Axial force leads to a “uniform distribution” of normal stresses

What is the method to find a normal stress is tensile or compressive ?

Imagine a cut, isolate either the left or the right portion, sketch the remaining external forces (as well as internal forces), then calculates the axial force from the equation.

Finally, the normal stress is determined: is positive when “tensile” and negative when “compressive”:

Formula Axial Force

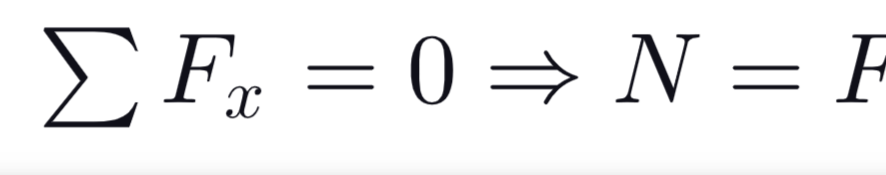
Normal Stress Formula

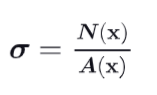
Formula Oblique Plane

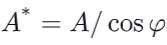
What are the 2 internal forces associated with an oblique section ?

• a normal component Fn acting perpendicular to the section

• a tangential component Ft acting within the place of the section.

Formula Normal Force

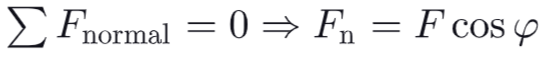
Formula Tangential Force

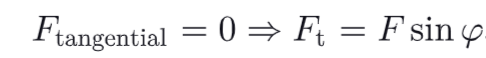
What are the 2 types of stresses developed in oblique cases ?

• a normal stress σ, which is the distribution of F, over the oblique plan

• a tangential or shear stress τ, which is the distribution of Ft over this oblique plane.

Formula Normal Stress σ

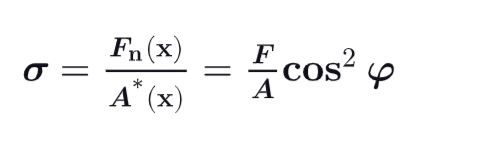
Formula Shear Stress τ

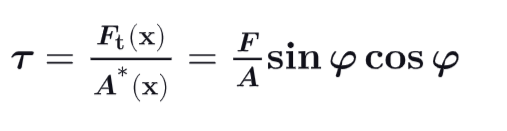
What is Normal Stress ?

It is mechanical effect developed when 2 neighbor surfaces are subjected to either a tensile or compressive effect trying to “separate” or to “merge” them.

What’s Shear Stress ?

It is the mechanical effect developed when 2 neighbor surfaces are subjected to transverse effect trying to “slide” one surface with respect to the other.

Formula Engineering Strain

Δl : change in length

l0​ : original length

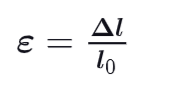
What does Shear stress cause to an element ?

A change “shear strain” or “shear distortion” in angle relative to the original non-deformed element.

It is denoted by the symbol γ and expressed in rad

Assumption : shear strain is distributed equally between rotations of the horizontal and vertical sides of the rectangle

Formula Shear Strain/ Shear Distortion

The shear strain is :

• positive for an acute parallelogram angle

• negative for an obtuse parallelogram angle.

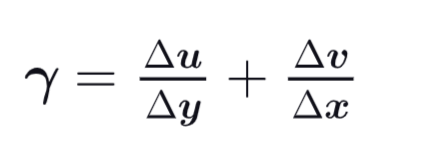
What’s Hooke’s Law ?

established experimentally, expresses the relationship between the applied normal stress and the resulting normal strain in a solid material.

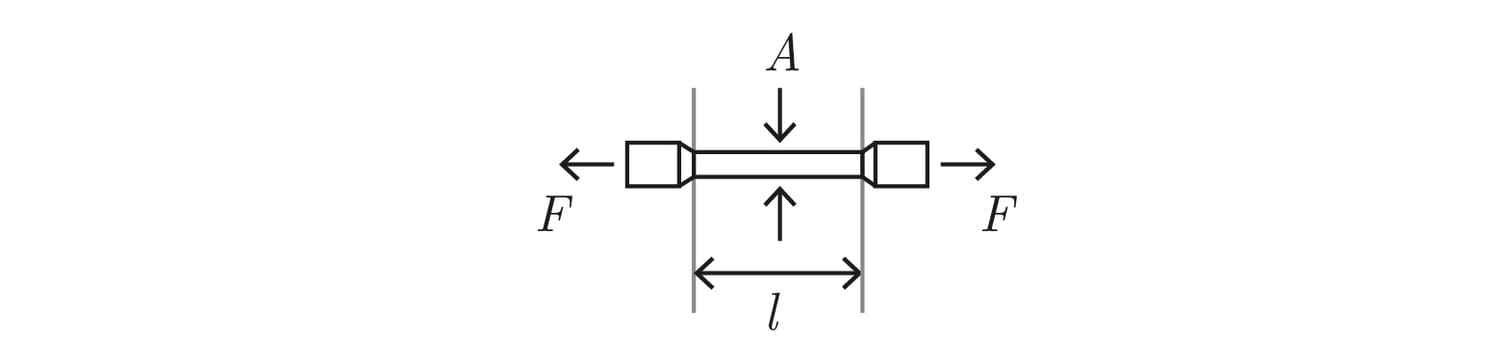
Describe the Specimen used for the Stress-Strain experiment.

Name l

l : gauge length

How do you find the law of Behavior of a Ductile Material ?

• Using a “bone shaped” specimen

• Value of F is increased by a constant amount within a constant interval of time at a very low speed

• For each value of F; the elongation Δl is also recorded.

• The increment of F and the related measurements continue until a complete fracture of the specimen occurs.

• For each recorded value of F and Δl , the corresponding normal stress and normal strain are calculated, such that and .

• The stress–strain diagram is plotted : It is the “law of behavior” of the material.

Formula Linear Elastic Behavior

For low strain levels, the stress increases in a linear manner (proportionality)

• Stress: σ

• Modulus of Elasticity (Young’s Modulus) E

• Strain : ϵ

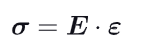
What is E ?

• Modulus of Elasticity (Young’s Modulus)

• It is a property unique for a material

• expresses the theoretical amount of stress needed to cause a strain equal to unity. (Pa)

• It shows its ability to resist deformation under a certain level of applied stress.

How long is Hooke’s Law valid for ?²

As long as the stress level is under the particular value σY “yield strength”

it is the highest value of stress that might be applied without altering the elasticity.

What happens for the specimen once it reaches the yield strength ?

Above yield strength, the material enters a “plastic behavior” region, an “unsafe” region in engineering mechanics

However, the stress is still increasing with the strain (but in a non-linear manner)

What is the utimate strength ? What happens in the specimen ?

σU

In this region, when the load is removed, only a part of the strain is given back, while another part is retained permanently: This is the “plastic strain.”

The plastic behavior between yield and ultimate strength is known as “strain hardening,”

Strain Hardening Formula

The strain hardening modulus and the strain hardening exponent depend on the type of material.

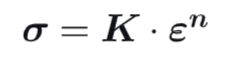
What happens beyond The Utimate Strength ?

The engineering strain continues its increment despite the engineering stress decreasing

This second part of the plastic behavior is termed “necking.”

What is a Shear Test ?

Same as a Tensile Stress

Hook’s Law Shear Stress

τ : shear stress

G : “shear modulus,” “Coulomb’s modulus,” “modulus of rigidity.”

γ : shear strain

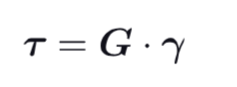
What’s the difference with the Engineering Stress and the True Stress ?

In reality, the cross-sectional area is decreasing during the test as F increases, the normal stress is calculated relative to the initial cross-sectional area.

This is known as “engineering stress” and is used as a conventional value.

“True stress” is calculated by dividing each level of force by the actual real value of the area, which decreases throughout the test; this quantity is rarely used in mechanics.

(The same principle applies to the strain.)