Maths

Not finished

The Trapezium rule

Area = 0.5 h (y0 + y3 + 2 (y1 + y2)

First + last + (2 x rest)

Variable acceleration

Integrate Integrate

S V A

Differentiate Differentiate

Simple random sampling

Takes a random selection from the population to use as a sample. The entire population must be known and identifiable. Each random sample will be different and some will contain bias. The probability of a strongly biased sample is reduced as sample size increases.

Stratified sampling

If the parent population has clear subgroups, it is possible to take a sample. The quick calculation to determine the number for each subgroup to be randomly selected as part of the sample is: (number in subgroup/ number in population) x sample size. This technique requires a lot of information to begin about the population.

Quota sampling

Similar to stratified, though the ‘quota’ of items to be included from different subgroups isn’t necessarily proportional. It also doesn’t require a random sample from within the subgroup, so bias is extremely likely.

Systematic sampling

A method where a sample is selected from a population at regular intervals; for example, every 10th individual in a list. This method is straightforward but can introduce bias if there's a hidden pattern in the population.

Midpoints

((X1+X2)/2), ((Y1+Y2)/2)

Distance between two points

√((x_2-x_1)²+(y_2-y_1)²)

Gradient of a chord

Y2-Y1/X2-X1

Parallel lines

The same gradient

Perpendicular lines

Negative reciprocal gradient

Y intercept

When X=0

X intercept

When Y=0

Perpendicular bisector

1) midpoint

2) neg recip gradient

3) Y-Y1= M(X-X1)

4) rearrange into Y=MX+C

Quadratic formula

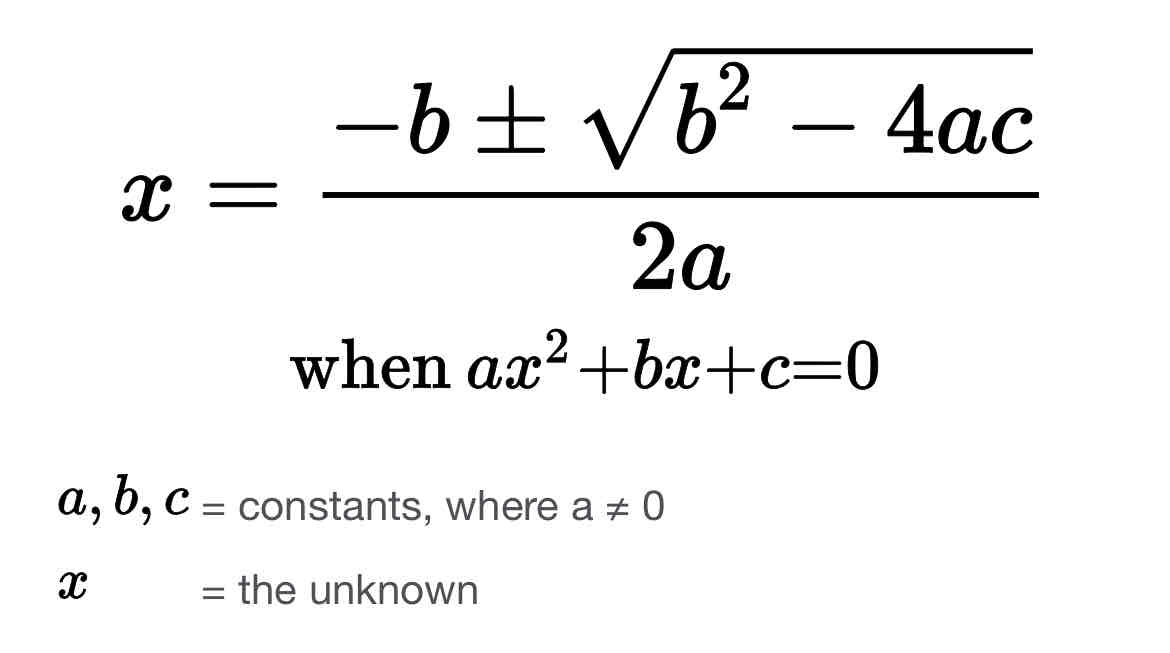
Discriminant

B²-4ac

One real root

When the discriminant = 0

Two distinct roots

When the discriminant > 0

No real roots

When the discriminant <0

Two rational roots

Perfect square

(X+ 1/2b)² +0

1000= 10³

Log10(1000)=3

LogbB

1

Logb1

0

LogcA+logcB

LogcAB

LogcA-logcB

LogcA/B

Logc(A^B)

BlogcA

Logc√A

1/2logcA

LogeX

lnX

If f(a/b) = 0

Then (bx-a) is a factor

If it isn’t a factor

It is a remainder

Remainder Theorem

The Remainder Theorem states that if a polynomial f(x) is divided by (x-a), the remainder is equal to f(a). This can be used to quickly find remainders without completing the full division.

Y=X

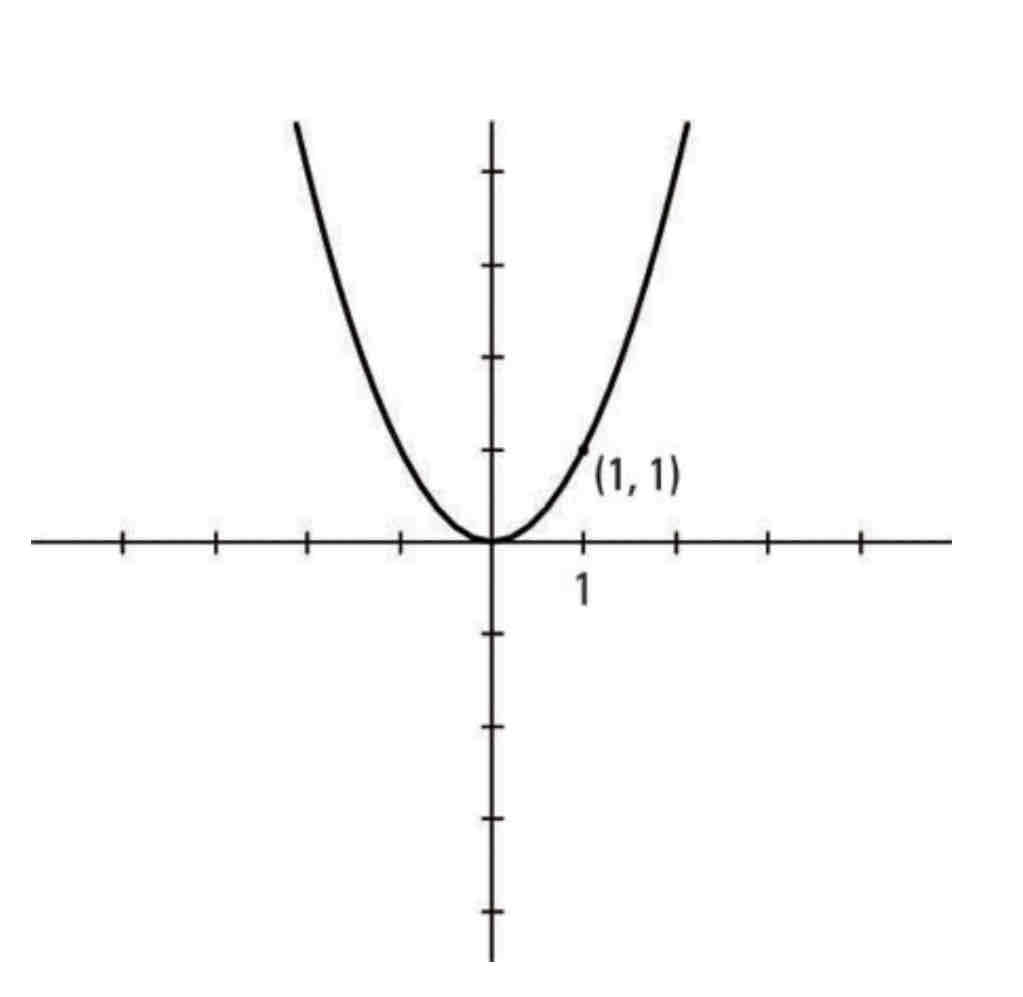
Y=X²

Y=X³

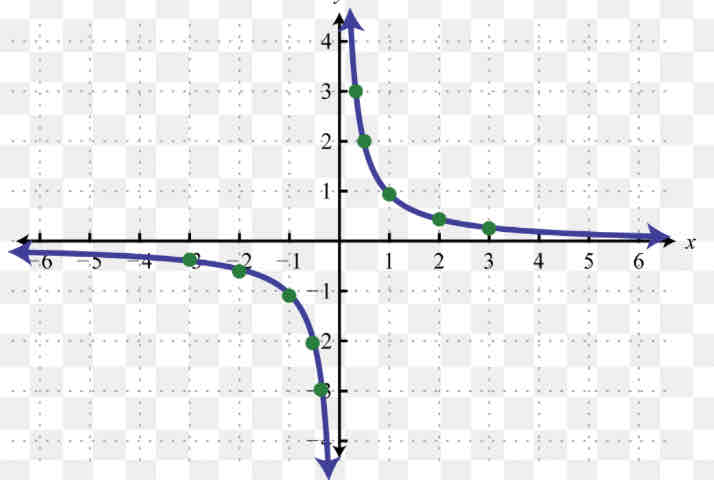
Y= 1/X

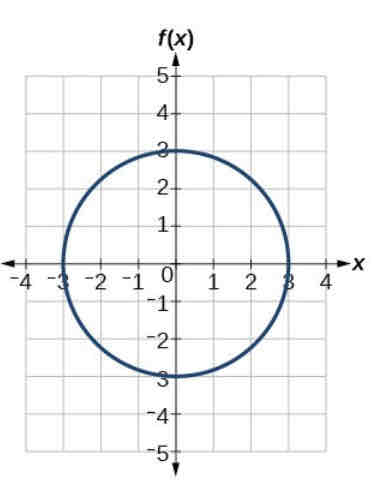
Y²+X²=r²

Translation of Y=f(x) by the vector [ab]

Y=f(X-a)+b

Stretch on the x axis by the factor k

Y=f(1/k X)

Stretch on the Y axis by the factor K

Y=KF(X)

Reflection on the x axis

Y= -f(x)

Reflection on the y axis

Y=f(-X)

Reflection on y=x

Swap the x and y

Eg. Y=f(x) ↦ X=f(y)

Finding the centre and radius of a circle

Complete the square

Circle theorem

If <ABC = 90°, then AC is a diameter of the circle with A,B,C on the circumference

Tangent

Line touching a circle at a distinct point

Normal

Line perpendicular to tangent

Given Y= ab^x

Log10Y= log10A+ log10B

Exponential curve

Log10Y and X

1) take logs of both sides

2) simplify

Gradient= log10b

Y intercept = log10a

Y=aX^b

Log10Y= log10A+Blog10X

Polynomial line

Log10Y and log10X

1) take logs of both sides

2) simplify

Gradient= b

Y intercept = log10a

Natural numbers

Positive integers

Integers

All numbers on the numberline

Rational numbers

Fractions

Reals

All numbers you can think of (π, e, 1/3, √2, 500, -2)

Set notation

{x:x ∈ R, a<x<b}

Interval notation

x ∈ (a,b)

( is not including

[ is including

Differentiation in first prinicples

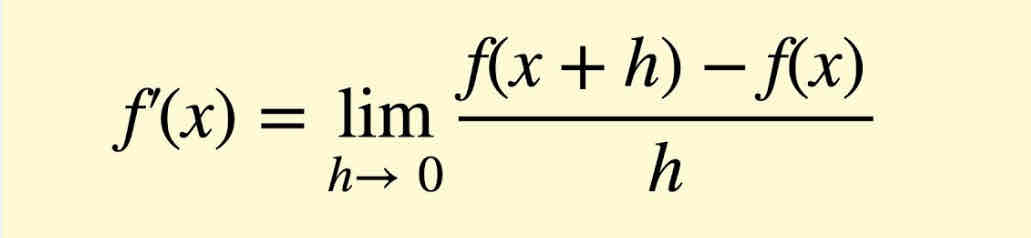
Average speed

Total distance

———————

Time

Average velocity

Total displacement

—-————————

Time

Velocity- time graph into acceleration-time

Acceleration= gradient of velocity

Circle property diameter

The triangle formed from the ends of a diameter has a right angle

Circle property chord

The perpendicular from the centre to a chord bisects the chord

Circle property tangent

A tangent to the circle meets a radius at a right angle

Sin2x

2sinxcosx

Cos2x

1. Sin²x-cos²x

2. 1-2sin²x

3. 2cos²x-1

Tan2x

2tanx

---

1-tan²x

Cosec²x

1+cot²x

Sec²x

1+tan²x

Cosecx

1

---

Sinx

Secx

1

---

cosx

Cotx

1

---

tanx

Tanx

Sinx

---

cosx

Cotx

Cosx

---

sinx

Moment- clockwise

Negative NM

Moment- anticlockwise

Positive NM

What is a resultant moment

The sum of all moments acting on a particle (negative and positive)

Finding resultant moment

1. Decide which force direction is clockwise and anticlockwise.

2. Work out each moment.

3. Sum all together and subtract clockwise moments.

4. The overall value is the resultant moment.

When a moment is in equilibrium

The resultant force is 0N and the resultant force about any point is 0NM

Solving problems with moments in equilibrium

1. Identify ALL perpendicular distances and ALL forces from the pivot

2. Use the fact that resultant force is 0 in the equation and the fact that the resultant moment is 0 in the other equation

3. If you have an unknown force you can pick a pivot point that is on the same “line of action” so that unknown force is 0NM

4. Solve equations

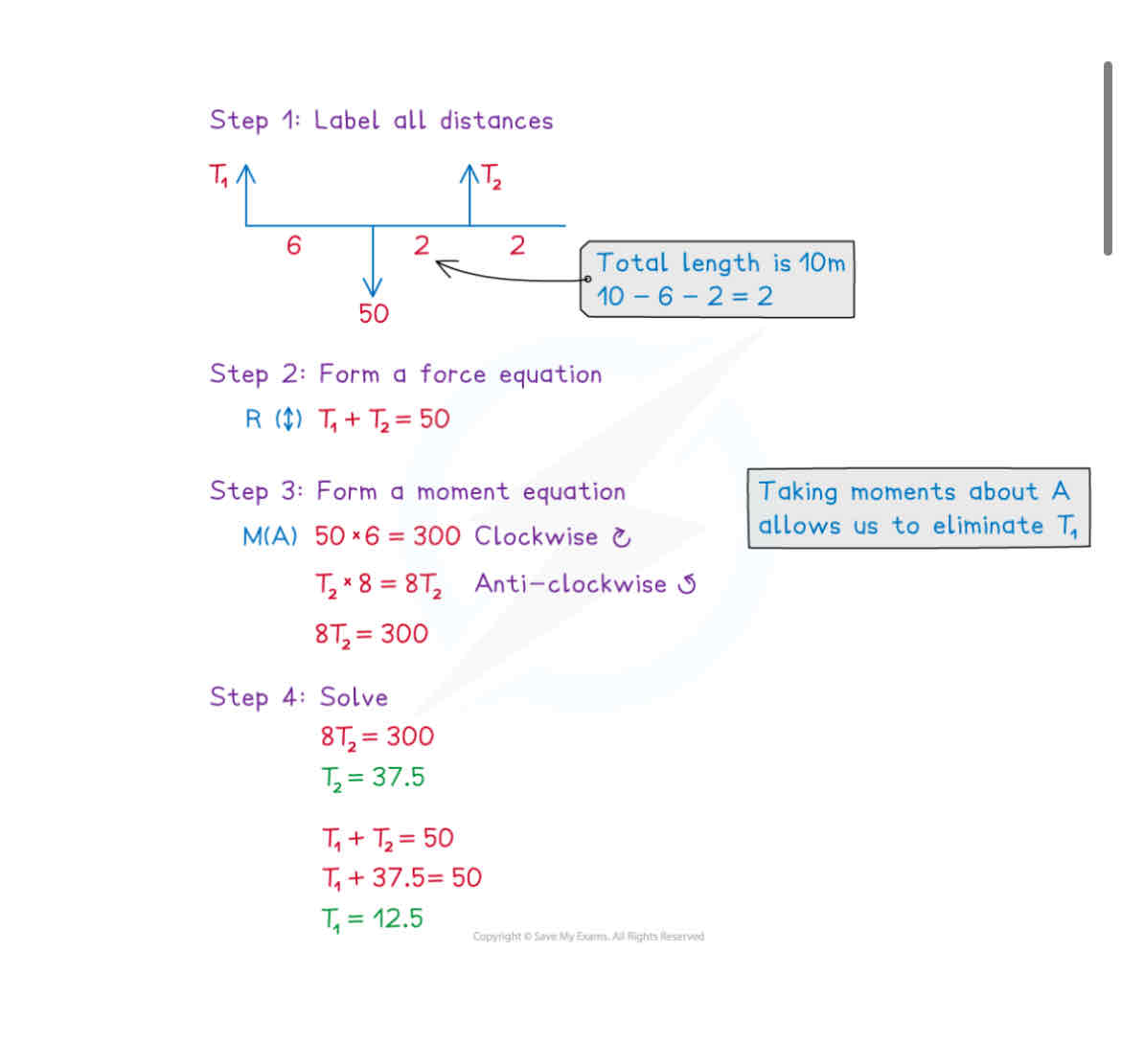
Method for Solving A Level Maths Question on Tilting Rods using Moments

1. Identify all forces acting on the rod. 2. Calculate the moment for each force (Moment = Force x perpendicular distance). 3. Determine the pivot point. 4. Sum the clockwise moments and anticlockwise moments. 5. Set the total moments equal to zero for equilibrium. 6. Solve the resulting equation for unknown forces.

A³ x A²

3+2=5 so A^5