Merge Sort

Divide and Conquer Paradigm

• The core idea is to decompose a problem into simpler sub-problems (of the same type)

• Then, solve recursively on the sub-problems

• Finally, combine the solutions for the sub-problems to get a solution of the original problem

Divide and Conquer in Merge Sort

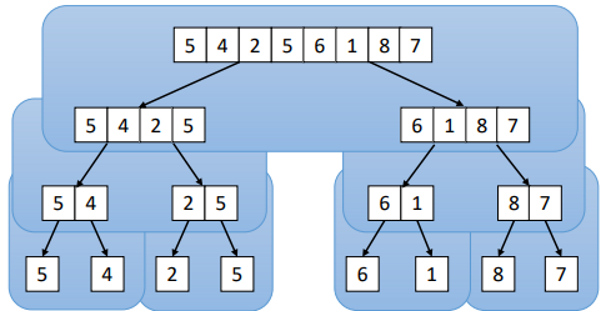
• Split: Split the input array into two equal halves

• Solve: Recursively solve (i.e., sort) the two subarrays independently

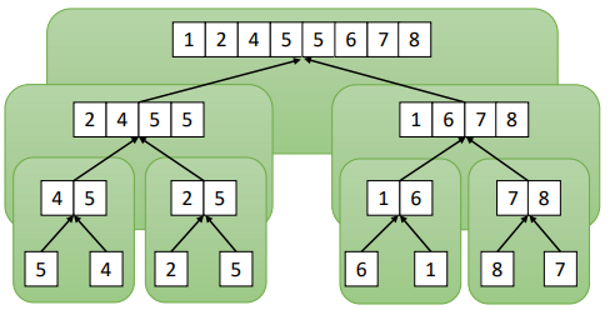
• Combine: Combine the two sorted subarrays by merging to get an overall sorted array

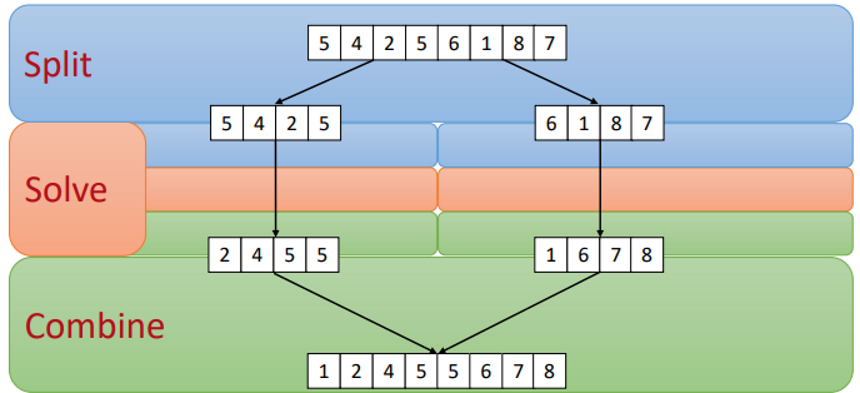
Top-Down Splitting

Bottom-Up Merging

Code

class MergeSort {
   static void mergeSort(int array[]) {
      int[] tmp = array.clone();
      recursiveMergeSort(tmp, 0, array.length - 1, array);
   }

   static void recursiveMergeSort(int B[], int iStart, int iEnd, int A[]) {
      if (iEnd == iStart) {
         return;
      }
      int iMid = (iStart + iEnd + 1)/2;
      recursiveMergeSort(A, iStart, iMid - 1, B);
      recursiveMergeSort(A, iMid, iEnd, B);
      merge(B, iStart, iMid, iEnd, A);
   }

   static void merge(int A[], int iStart, int iMid, int iEnd, int B[]) {
      int i = iStart;
      int j = iMid;
      for (int k = iStart; k <= iend; k++) {
         if (i < iMid && (j > iEnd || A[i] <= A[j])) {
            B[k] = A[i];
            i++;
         }
         else {
            B[k] = A[j];
            j ++;
         }
      }
   }
}

Correctness

for inputs of size ≤ n

for the easier merge sort, that creates temporary arrays in each split step

• Prove by (strong) induction that Correctness(n) is true for all 𝑛 ≥ 1

• Base step (for 𝑛 = 1): 

  • Correctness(1) is clearly true, as an array with one entry is already sorted

• Induction step (for 𝑛 > 1): 

  • First, assume that the induction hypothesis holds for all integers 𝑛′ ≥ 1, 𝑛′ < 𝑛

  • Recall that Merge Sort splits an input array of size 𝑛 into two smaller arrays of size 𝑛/2 < 𝑛, and then recursively runs Merge Sort on each smaller array

  • The induction hypothesis holds for 𝑛/2 so the recursive calls return sorted arrays

  • Finally, the merging function successfully combines the two smaller, sorted arrays into the sorted version of the input array (of size 𝑛)

Worst-Case Time Complexity

for the easier merge sort, that creates temporary arrays in each split step

Cost of Operations: 

• Merging two arrays, of size 𝑘 each, takes 𝑐1𝑘 elementary operations

• Splitting an array of size 𝑘 takes 𝑐2𝑘 elementary operations

Time Complexity:

• 𝑇𝑀(𝑛) is time complexity of Merge Sort when run on an input of size 𝑛

• 𝑇𝑀(𝑛) ≤ 2𝑇𝑀(𝑛/2) + (𝑐1 + 𝑐2) ⋅ 𝑛

Justification:

• First, we split the array of size 𝑛

• Then, we run Merge Sort on two different arrays, each of size 𝑛/2

• Finally, we merge the two small (𝑛/2-sized) arrays

Analysis Summary

• Best case - O(nlog(n))

• Average case -  O(nlog(n))

• Worst case -  O(nlog(n))

• In-place - no

(best case and average case are implied by the worst case upper bound)