AQA A-Level Computer Science - Data Structures and Abstract Data Types

Data Structures

Containers that store different types of data.

Arrays

Indexed set of related elements.

Must be finite, indexed, and only contain elements with the same data type.

Abstract Data Types / Data Structures

Make use of other data structures to form a new way of storing data. Do not exist as data structures alone.

Queues

Abstract data structure based on an array.

Referred to as "first in, first out" (FIFO) abstract data structures.

Uses of Queues

Used by computers in keyboard buffers - each keypress is added to the queue and removed when the computer has processed the keypress.

Ensures the letter appear on the screen in the same order they were typed.

Linear Queues

Has two pointers (front and rear), to identify where to place a new item in a queue / identity which item is at the front.

Rear always points to the next available position in the queue.

Circular Queues

The front and rear pointers can move over the ends of the queue for a more memory efficient data structure and utilise any spaces left at the front of the queue.

Queue Operations

Enqueue - Add an item to the end of the queue.

Dequeue - Remove an item from the queue in FIFO order.

IsEmpty - returns TRUE if the queue has no content by comparing if the front and rear pointers are equal to each other.

IsFull - returns TRUE if the queue has no available positions that are behind the front pointer.

Priority Queues

Items are assigned priority. Items with highest priority are dequeued before low priority.

If items have same priority, FIFO applies.

Uses of Priority Queues

Processors assign time to applications according to their priority. Application currently used by the user are prioritised over background applications for a faster user experience.

Stacks

First in, Last out (FILO) abstract data structure.

Often based on an array, but only have one (top) pointer.

Stack Operations

Push - Add an item to the stack

Pop - Remove the item at the top of the stack

Peek - Returns the value of the item at the top of the stack but does not remove it.

IsEmpty - returns TRUE if the stack has no content.

IsFull - returns TRUE if the stack has no available positions that are behind the top pointer.

Graphs

Used to represent complex relationships between items within datasets.

(Transport + IT networks, the Internet)

Features of Unweighted, Undirected / Weighted, Directed Graphs

Consists of nodes (or vertices) joined by edges (or arcs .

Weighted graphs have assigned values to edges, representing values such as time, distance or cost.

Adjacency Matrices

Tabular (Table) representation of a graph. Each node of a graph is assigned a row and column in a table. Stores all edges / connections, even edges that don't exist.

Features of Adjacency Matrices - Unweighted Graph

1 - An edge exists between two nodes

0 - No connection between two nodes (or is the same node)

All adjacency Matrices display diagonal symmetry.

Features of Adjacency Matrices - Weighted graph

Contains the weight of the connection between two nodes instead of Boolean values.

If no connection exists, an extremely large value is used to prevent a shortest path algorithm from using edges that don't exist - often expressed as infinity.

Adjacency Lists

List representation of a graph. For each node in the graph, a list of adjacent nodes is created - only recording existing connections in a graph.

Pros of Adjacency Matrix

Allows an edge to be queried very quickly, as it can be looked up by its row and column.

Suited to dense graphs with large number of edges.

-> Time efficient

Cons of Adjacency Matrix

Stores every possible edge between nodes, even those that don't exist.

Almost half of the matrix is repeated data.

-> Memory inefficient

Pros of Adjacency lists

Only stores the edges that exist in the graph.

Suited to sparse graphs, where there are few edges.

-> Memory efficient

Cons of Adjacency lists

Slow to query, as each item in a list must be searched sequentially until the desired edge is found.

-> Time inefficient

Trees

Connected undirected graph with no cycles.

Rooted Trees

Has a root node from which all other nodes stem - usually at the top of the tree.

Parent nodes

Nodes from which other nodes stem.

(The root node is the only node in a rooted tree with no parent.)

Child nodes

Nodes with a Parent.

Leaf nodes

Child Nodes with no children.

Rooted Trees: Binary Trees

A rooted tree in which each parent node has no more than two child nodes.

Hash Tables

A way of storing data that allows data to be retrieved with a constant time complexity of O(1).

Hashing Algorithm

Takes an input and returns a hash. A hash is unique to its input and cannot be reversed to retrieve the input value.

The same hash is always returned for each input.

Storing in Hash Tables

Hash table stores key-value pairs.

The key is sent to a hash function that performs arithmetic operations on it. The resulting hash is the index of the key-value pair in the hash table.

Looking up elements in Hash Tables

The key is first hashed.

Once the hash has been calculated, the position in the table corresponding to that hash is queried and the desired information is located.

Collision

When different inputs produce the same hash.

Could result in data being overwritten in a hash table.

Rehashing Algorithm

Finding an available position according to an agreed procedure.

Example: Keep moving to the next position until an available one is found.

Dictionary

A collection of key-value pairs in which the value is accessed by its associated key.

"row, row, row your boat"

1 - row

2 - your

3 - boat

Dictionary-based compression = 11123

Vectors

Represented lists of numbers, functions or ways of representing a point in space.

Vectors viewed as a function...

Represented using a dictionary.

Vectors viewed as a list....

Represented using a one-dimensional array.

Vector Addition

Vectors added to show a translation.

Vectors can be added 'tip to tail' with arrows.

Alternatively, vectors can be added by adding each of their components - [14,4] + [4, -2] = [18, 2]

Scale-Vector Multiplication

To scale a vector, each of its components are multiplied by a scalar, affecting magnitude and not direction.

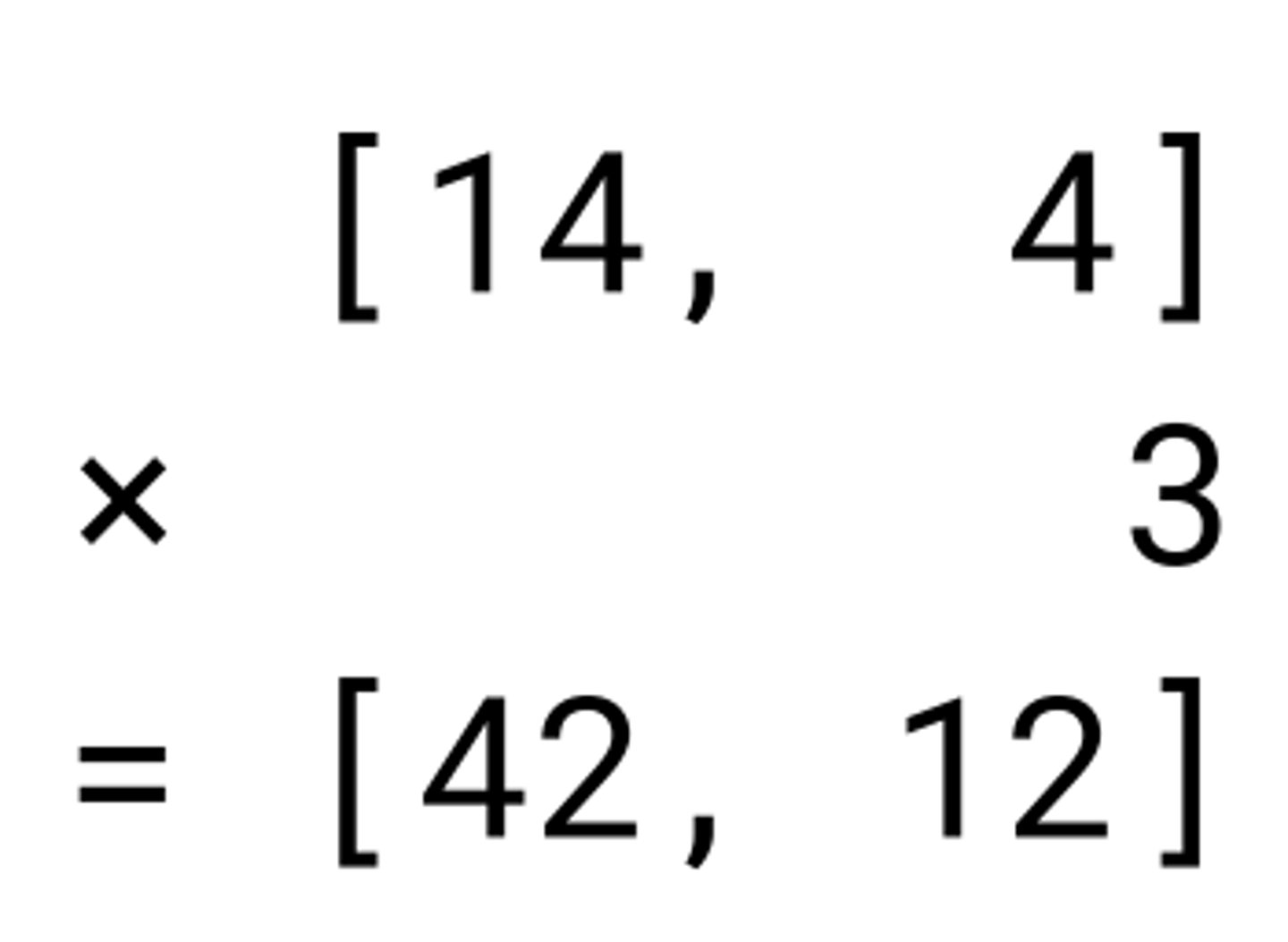
Convex combination of two vectors

Vector 1 = a

Vector 2 = b

Convex combination = ax + by

Where:

x != 0 and y != 0

x < 1 and y < 1

x + y = 1

Dot Product / Scalar Product

A single number derived from the components of the vectors.

Can be used to determine the angle between two vectors.

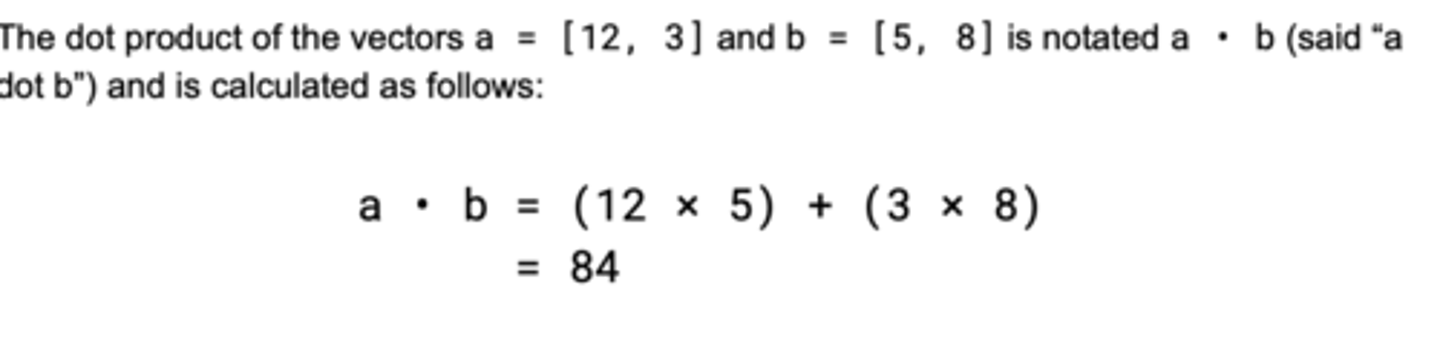
Static Data Structure

Fixed in size.

Declared on memory as a series of sequential, contiguous memory locations (Next element will be in the memory location next door).

If number of data items to be stored exceeds the number of memory locations allocated, an overflow error/ stack overflow will occur.

Dynamic Data Structure

Changes size to store content.

Each item of data is stored with a reference to where the next item is stored in memory.

If the number of data items to be stored exceeds the number of memory locations allocated, new memory locations are added until there is enough space for the data.