MATH 239 Graph Theory Theorems

Handshaking Lemma

Theorem: If there exists a walk from vertex x to y in G, then there exists a path from x to y in G

Theorem: Let G be a connected graph. G has an Eulerian Circuit if and only if every vertex in G has even degree

Lemma: If connected graph G has bridge e = uv, then G-e has exactly 2 components and u, v are in different components

Theorem: An edge e is a bridge of graph G if and only if it is not contained in any cycle

Theorem: If G is a non-empty graph such that |E| >= |V| then G has a cycle

Theorem: If T is a tree, then |E| = |V| - 1

Corollary: For any non-empty tree T, Σ(deg(v) - 2) = -2

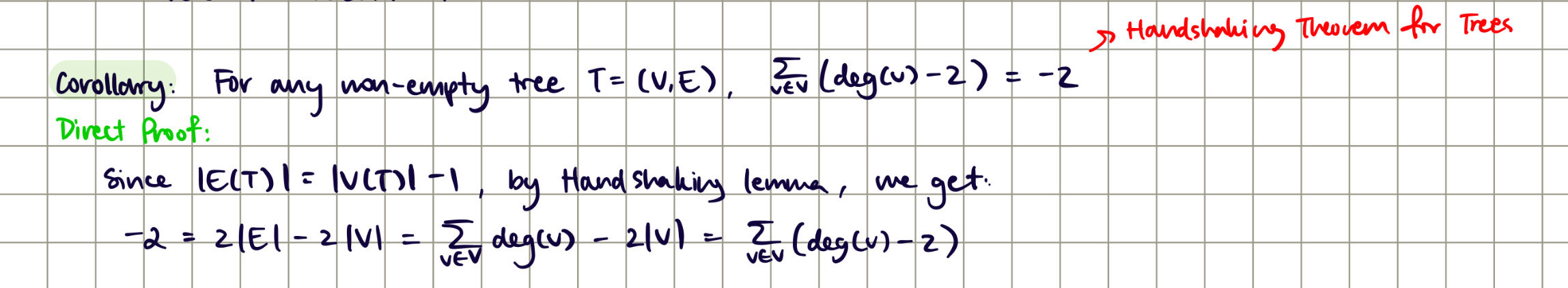
Theorem: A graph is connected if and only if it has a spanning tree

Lemma: If graph G is not bipartite, then G has a cycle of odd length

Lemma: Every cycle in a bipartite graph has even length

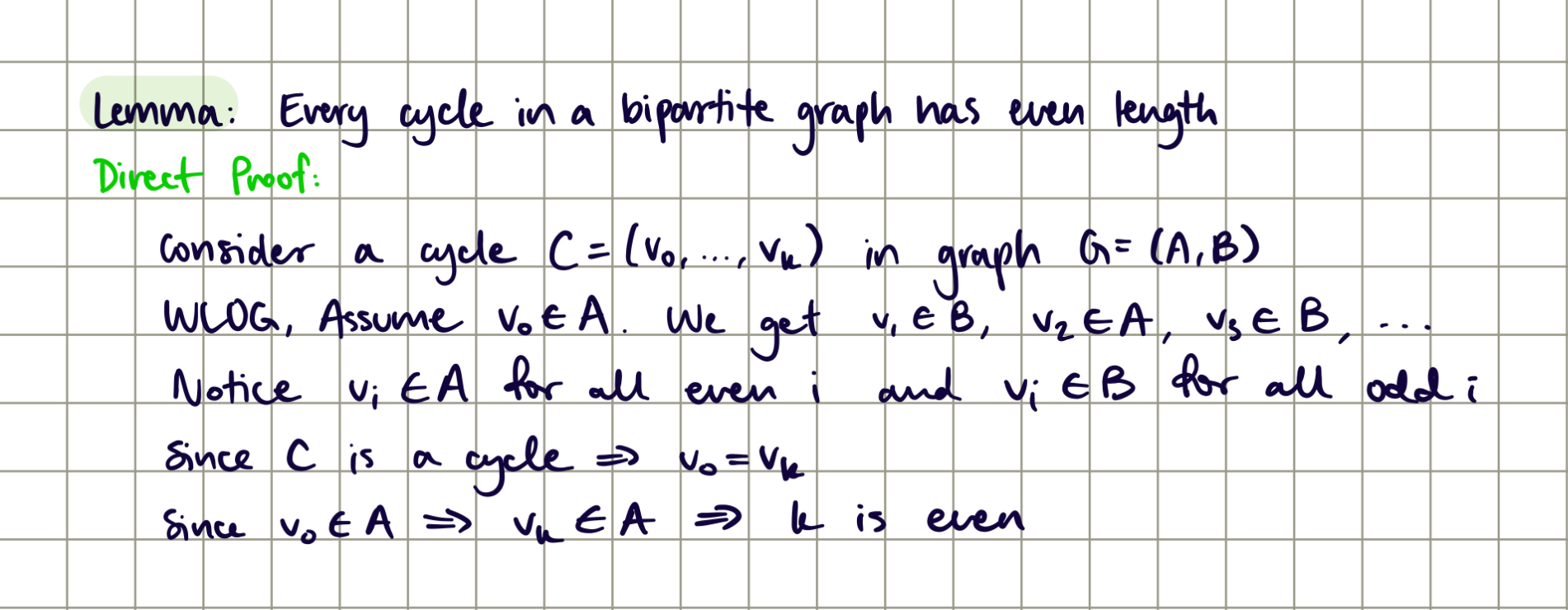
Theorem: A graph is bipartite if and only if it has no cycles of odd length

Faceshaking Lemma

Euler’s Formula: Given planar graph G, |V| - |E| + |F| = |C| + 1

Lemma: If G is a planar embedding whose faces all have degree at least d* >= 3, then |E| <= (d*/d*-2)(|V|-2)

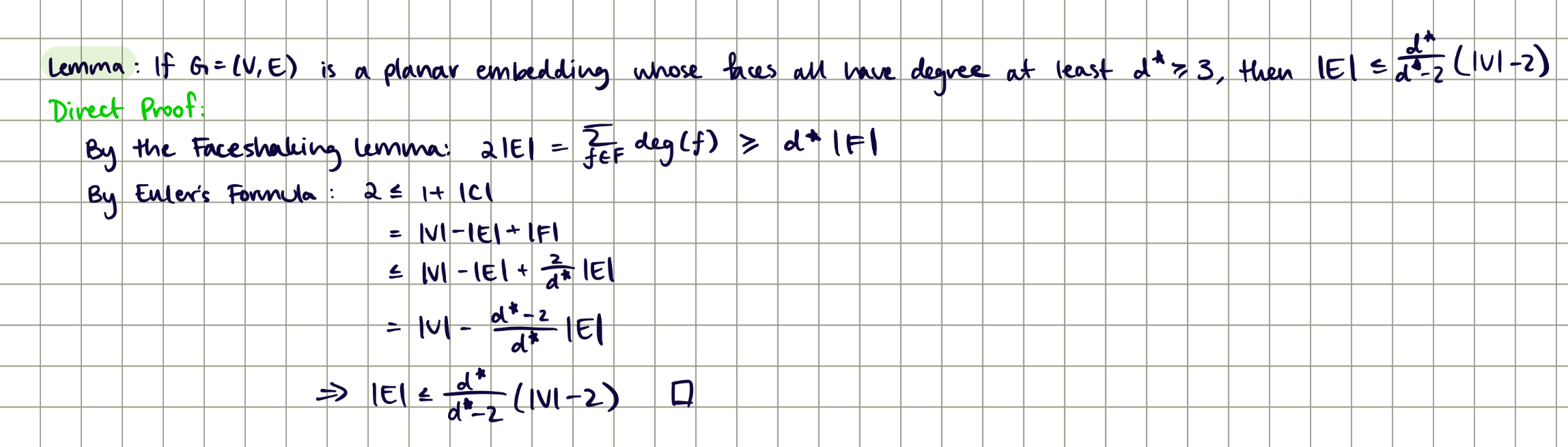
Corollary: Every planar embedding has either:

1. A vertex of degree at most 5

2. A face of degree at most 2 (degenerate face)

Theorem: Let G be a planar graph with |V| >= 3. Then |E| <= 3|V| - 6

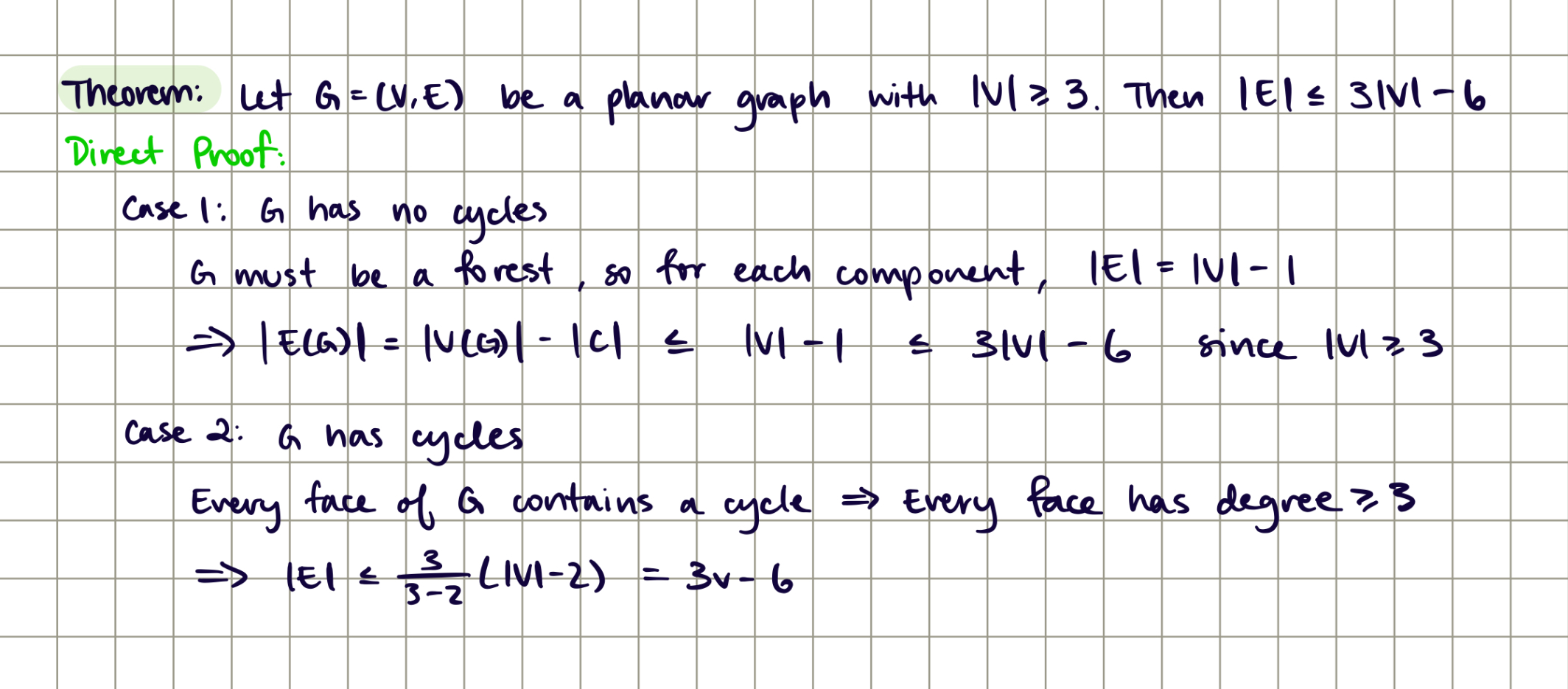
Kuratowski’s Theorem

6-Colour Theorem: Every planar graph is 6-colourable

5-colour Theorem: Every planar graph is 5-colourable

Lemma: If M is a matching of G and C is a cover of G then |M| <= |C|

Corollary: For matching M and cover C such that |M| = |C|, we have

1. M is a maximum matching

2. C is a minimum cover

Konig’s Theorem: In a bipartite graph, the maximum size of a matching is the minimum size of a cover

Hall’s Theorem: A bipartite graph G = (A,B) has a matching saturating every vertex in A if and only if every subset D ⊆ A satisfies |D| <= |N(D)|