Need to Know

Every element has a unique atomic number representing the

number of protons

Mass Number

Number of Protons and Neutrons

Mass Number is located where on an element

in the upper left corner of its symbol

Atomic number is located where on an element

in the lower left corner of its symbol

isotope

a variant of an element, having the same number of protons but different numbers of neutrons.

Protium

the most abundant hydrogen isotope, with one proton and no neutrons.

Deuterium

a hydrogen isotope with one proton and one neutron.

Tritium

a hydrogen isotope with one proton and two neutrons, known for its radioactive properties.

Iron has how many isotopes

31

Iron has how many stable isotopes

4 stable isotopes: Fe-54, Fe-56, Fe-57, and Fe-58.

There are about ____ known naturally occurring and synthetic isotopes

3000

there are predicted to be up to ____ isotopes that could possibly exist

7000

How many isotopes are stable on Earth

250 and include only elements below Pb

Pb has the

Heaviest stable Isotopes

Smaller elements are stable with a

1:1 ratio of neutrons and protons

Large nuclei need

increasing numbers of neutrons for the isotopes to be stable

Fission

The splitting of large unstable isotopes. This is the basis for the first nuclear bombs as well as nuclear power plants

Fusion

The combining of small particles in a highly exothermic process. It occurs within the sun and is potentially the ideal source of clean nuclear power to solve the world’s energy crisis. Technological challenges have slowed progress on the development of fusion reactors

Radioactive Decay

The process by which the approximately 7000 isotopes decay to the 250 stable isotopes on Earth. There are many types of radioactivity that involve small particles like photons, protons, electrons, positrons, alpha particles, etc., to be emitted with a half-life that can be extremely fast or millions of years. The types of radioactive decay you need to be responsible for are: alpha decay, beta decay and gamma decay

Alpha particle (Notation)

Beta particle (Notation)

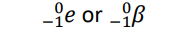
Gamma radiation (Notation)

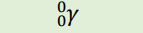
Neutron (Notation)

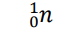
Proton (Notation)

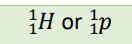
Positron (Notation)

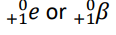
Alpha particle (Symbol)

α

Beta particle (Symbol)

β —

Gamma radiation (Symbol)

γ

Neutron (Symbol)

n

Proton (Symbol)

p

Positron (Symbol)

β +

Nuclear energies =

millions to billions of kJ/mol

Chemical bond energies =

100s to 1000s of kJ/mol

Intermolecular forces =

10s of kJ/mol

α decay

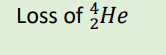
β decay

γ decay

α decay (Example)

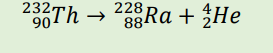
β decay (Example)

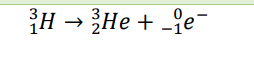
γ decay (Example)

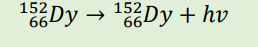
conservation of mass still applies here

the mass numbers on the left and right sides should add to the same number, and the protons on the left and right sides should add to the same number. Looking at β decay, for example: 3 + 0 = 3 (mass numbers) and 2 + (-1) = 1 (protons)

A common question is to be given the famous decay cycle

238U to 206Pb, which occurs by a 14-step process that will take billions of years to happen

A species’ half-life is

the amount of time it takes for the initial concentration of that species to be halved

0th order (half-life equation)

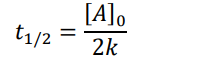
1st order (half-life equation)

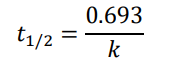
2nd order (half-life equation)

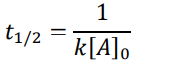
How to solve half life problems

Dividing by 2 because we’re dealing with half-life math here: 0.4 → 0.2 → 0.1 → 0.05 We divided by 2 three times to get from the start to the end. This means in 6 seconds, we used three half-lives. 6 seconds 3 half − lives = 2 𝑠𝑒𝑐𝑜𝑛𝑑𝑠 ℎ𝑎𝑙𝑓 − 𝑙𝑖𝑓𝑒 So, one half-life is 2 seconds.

Differential Rate Law: Rate Expression

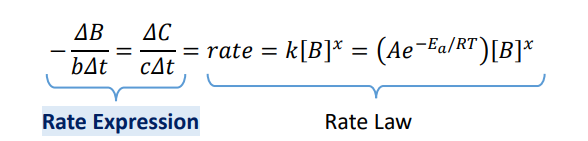
0th order (Rate Expression)

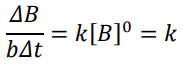
1st order (Rate Expression)

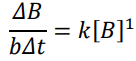
2nd order (Rate Expression)

0th order (Units)

Msec^-1

1st order (Units)

sec^-1

2nd order (Units)

M^-1sec^-1

Zeroth Order (Integrated Rate Law)

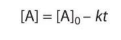
First Order (Integrated Rate Law)

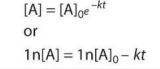
Second Order (Integrated Rate Law)

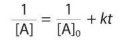
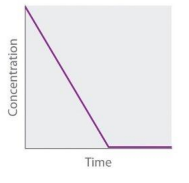
Zeroth Order (Concentration vs time graph)

First Order (Concentration vs time graph)

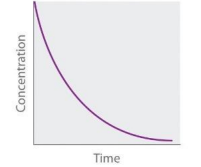
Second Order (Concentration vs time graph)

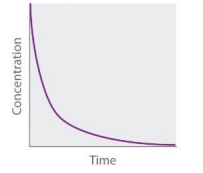
Zeroth Order (Straight Line plot to determine rate law constant)

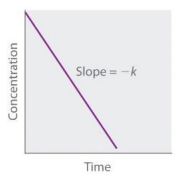
First Order (Straight Line plot to determine rate law constant)

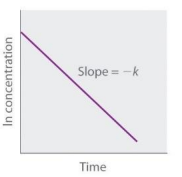
Second Order (Straight Line plot to determine rate law constant)

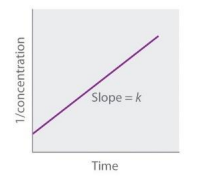
Method of Initial Rates (You got this down)

Integrated Rate Laws

Where [A]0 is the initial concentration, k is the rate constant, [A] is the concentration after some amount of time, t, and a is the coefficient in the reaction. If not explicitly provided, assume a = 1

Recognize that a straight-line formula follows the famous

y = mx + b equation, where y is the dependent variable (y-axis), m is the slope, x is the dependent variable (x-axis), and b is the y-intercept

Arrhenius equation

Where k is the rate constant, Ea is the activation energy, R is the gas constant, A is a constant called the pre-exponential factor, and T is the temperature

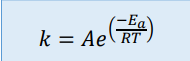
The pre-exponential factor is specific to the reaction

it represents the frequency of collisions between reactant molecules with the correct orientation for a reaction to occur

This equation highlights the relationship between the rate constant and temperature

as temperature increases, k increases. Logically this is because as the temperature gets higher, molecules have more energy to overcome the activation barrier to the reaction

Using two sets of data points, the equation can be expressed as

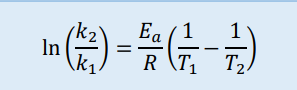
Arrhenius Equation

• This equation is similar to the van’t Hoff and ClausiusClapeyron equations.

• Activation energy (Ea) is the barrier to a reaction and is always

positive, on the order of about 5-500 kJ/mol.

• Thus, increasing T means k increases.

• Concentration vs time at two temperatures yields data that

can be plugged in to the equation to solve for Ea.

Combined Arrhenius Calculation

Collision theory is based on the

kinetic molecular theory of gases

This means 𝐾𝐸 = 1/2 𝑘𝑇 = 1/2 𝑚𝑣²

Collision theory says

collision must occur for the reaction to happen. (Note this does not explain first order decay.)

For the reaction to occur

the collision must be effective.

What determines an effective collision

This requires:

1. Sufficient energy to overcome the activation barrier (high enough temperature)

2. Correct orientation of collision

Transition states are

most easily depicted on reaction profiles of energy vs. time (reaction progress)

Transition State Theory is based on

energy, not collisions

In this profile (Transition State Theory)

an energy hill called the “activation barrier” rises positively above the thermodynamic profile

The barrier in transition State Theory is the reason why

spontaneous processes don’t happen without a source of energy (like why hydrogen balloons don’t explode unless they are touched by a flame)

The top of the activation barrier is the

“transition state” or “activated complex”. It is a theoretical structure. It is NOT an intermediate in the reaction

At the top of the energy hill

a transition state is equally likely to fall to the left or right

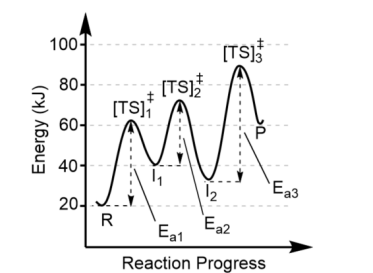
Reactants (R) are the

on the left

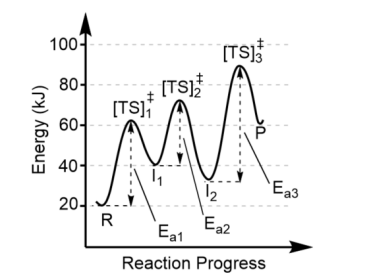
Products (P) are the

valley on the right

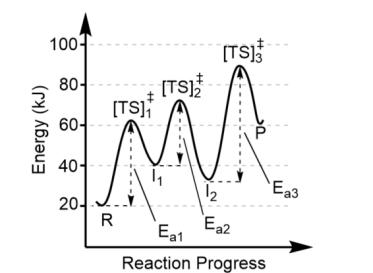
Transition states are found at

the top of each energy hill, [TS]‡

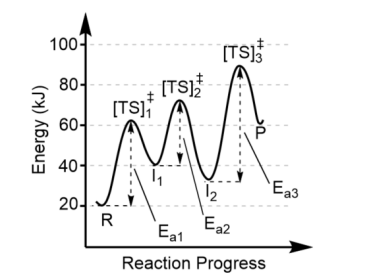
There is one transition state for

each step in the mechanism, thus this reaction has 3 steps (3 “hills” = 3 transition states)

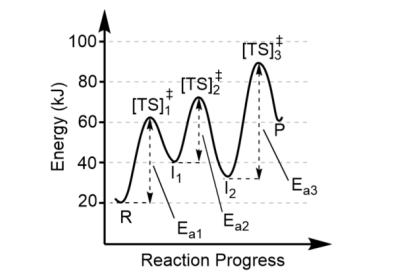
Each valley between reactants and products represent

the intermediates (I)

There can be more than one intermediate made, so the minimum number of intermediates is one less than the number of steps in the mechanism. Here, there must be at least two intermediates

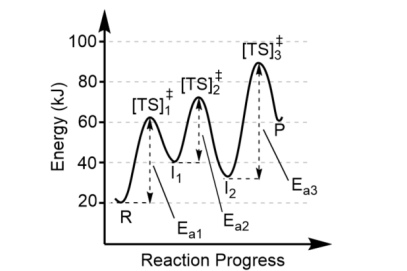
The largest activation barrier is associated with

the slow step, or the rate determining step, in the reaction. Here, that is Step 3 because Ea3 is the largest.

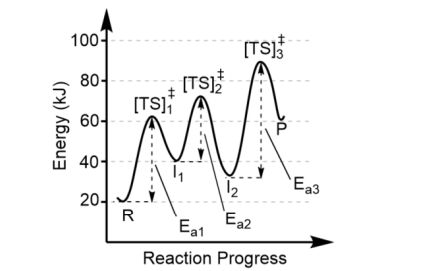
Note the forward reaction is

endothermic (Product energy – Reactant energy = positive

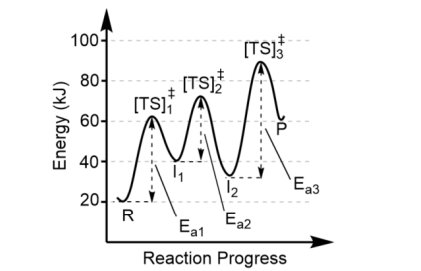
The reverse reaction is

exothermic

A catalyst typically shows up

as a reactant first and is then reproduced later in the reaction

an intermediate is

produced first then used up in a later step

To find the rate law given the slow step

first ignore everything from the products of that step and beyond. Then, cross out any remaining species that show up on both sides of the reaction arrow, and what’s left is the rate law

Rate Determining Step

Elementary Reactions

Given the reaction mechanism above, which species is a catalyst?

a) ClO

b) ClO2

c) NO2

d) None of these

e) N2O

D

Given the reaction mechanism above, what is the rate law?

a) Rate = k[NO2Cl]2[NO2]

b) Rate = k[NO2Cl]

c) Rate = k[NO2Cl]2[NO2]-1

d) Rate = k[N2O][NO2]-1

e) Rate = k[NO2Cl][NO2][NO2]-1

C

Ozone Layer Decomposition (Reactants)

2 O3 (g)

Ozone Layer Decomposition (Products)

3 O2 (g)

Ozone Layer Decomposition

Homogeneous chlorine radical, Cl•, catalyst