Math 152 Midterm

REMEMBER THESE

Distancce between vectors

||v-w||

another name for length

norm

Unit vector

1/||v|| * v

Dot product

v1*w1+v2*w2

Definition of the dot product

||v||*||w||*cos(θ}

v⋅w=0

orthagonal

orthagonal

perpendicular

The resuly of a dot product is a:

scalar

What is a scalar

A number

What is a vector

A set of numbers

Projection

What is a determinant?

A scalar associated with a square matric

Determinant of a 2×2 matrix

Geometic Representation of a 2×2 determinant

The area of the parallelogram created by the two vectors

The matrix of a determinant

Determinant of a 3×3 matrix

altermating + and -

How do you know the sign of a determinatn

Pos if it obeys the right hand rule

Cross product

ONLY R³

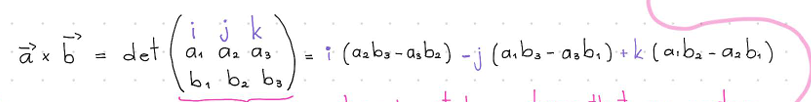
Geometrical interpretation of the cross product

axb is orthagonal to a and b

Area of parallelogram defined by cross product

the length of the cross product

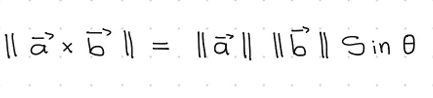
Triple product

The volume of a parallelpiped

The triple product of the 3 vectors

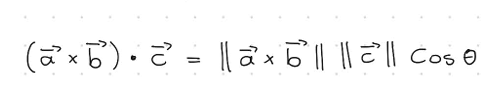
if det(a,b) = 0

a and b lie on the same line

if det(a,b,c) = 0

a and b and c lie on the same plane

Equation form of lines in R2

ax+by=c
where n=(a,b) is a normal vector, perpendicular to the line

Parametric from of lines in R2

x=p+td
where x p and d are vectors

p

a specific point on the line

d

a dierction vector

t

a parameter

when in doubt

solve for t

equation to parametric

set some variable to t and solve for the others

parametric to equation

solve for t for each equation and make them all equalv

vector from A

if you know a point and the normal, you can solve for anything

equation from for Planes in R3

Ax+By+Cz=D where n=(A,B,C)

parametric from for Planes in R3

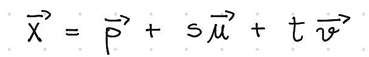
u x v

the n of a plane

distance from point to plane

Equation from for Lines in R3

a1x+b1y+c1z=d1

a2x+b2y+c2z=d2

Parametric from for Lines in R3

x=p+td

equation form to parametric form lines in R3

set t to 0

What are soolutions of linear equations

intersects

Linear independence

when the only way to make vectors equal to zero is to muliply them ALL by 0

Linearly dependednt

nontrovial combination, each vector can be written in terms of each ohter (at least one vector must be non zero)

Linear dependency in R2

v1=kv2

k=k

Linear dependecy in R3

Determinant = 0

what does ld mean in 2d?

colinearw

What does ld mean in R3

Same plane

what does li mean in 2d

All points can be written as x=rV1+sV2 (basis)

what does li mean in 3d

All points can be written as x=rV1+sV2+tV3 (basis)

3 types of solutions for any linear system

one unique solution —> find the solution

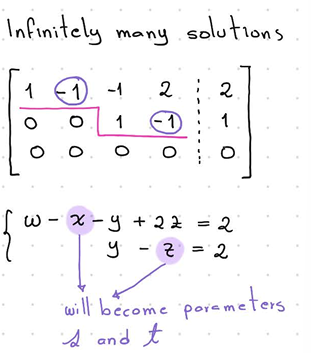
Infinitely many solutions —> find a parametric for all solutions

No solutions

3 operations that can be used to solve a linear system

1) interchanging 2 eqauations

2) Multiplying an equation by a scalar

3) Adding a multiple of an equation to another

Gauss elimation

turned a linear system in augmented from into a from where the solution is easy to find

Augmented matrix

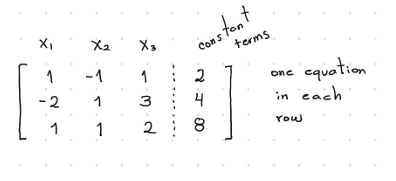
REF

Vectors go down in steps

anythings under the stars should be 0

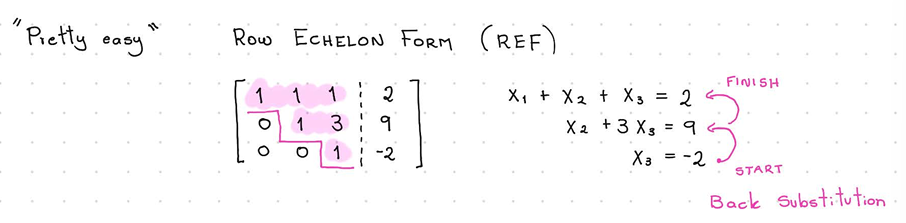
RREF

only 1s and 0s going down in steps

Unique solution

a varibale is equal to a number

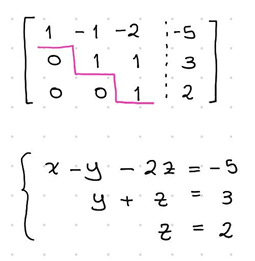
No solution

one is equal to zero, the other isnt

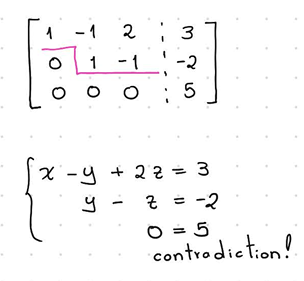
infinately many solutions

both are zero