Chapter 13: Oscillations About Equilibrium

Periodic Motion

• motion that repeats at regular intervals over time

• swinging pendulums, vibrating strings, and oscillating springs

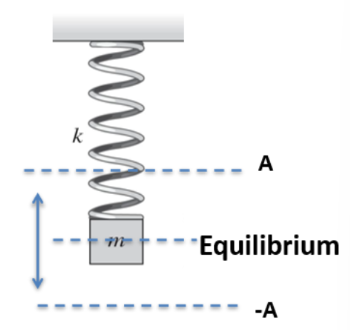
Periodic Motion Graph

• displacement over time

• A: amplitude/max displacement from equilibrium position (m)

• lambda: wavelength, size of wave for full cycle (m)

• T: time period of a complete cycle of period motion (s)

• f = # of complete cycles/oscillations per second (Hz)

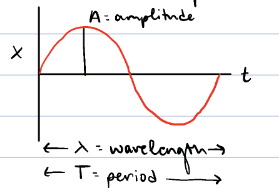
What is the period and frequency of a second hand on a clock?

• T = 60 s

• f = 1/60 = 0.017s^-1 = 0.017 Hz

A leaky faucet drips 40 times in 30 seconds. What is the frequency?

• f = 1/T = 40 times/30 s = 1.3 Hz

A mass on a spring in oscillation has amplitude A and period T. What is the total distance traveled by the mass after a time interval T?

• mass moves from its maximum displacement at A to the equilibrium position and back to A

• pendulum is easier to visualize

• 4A

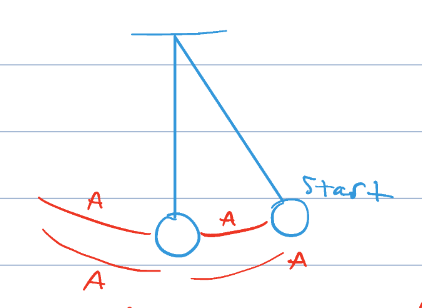
Simple Harmonic Motion

• motion back and forth around an equilibrium

• obeys Hooke’s Law

• F_s = -kx

  • F is proportional but opposite to x (SHM)

• If a force (on object) is proportional to displacement but opposite in direction, then the object’s motion is SHM

  • applies to small angles

• Applying a force F_x stretches the spring a distance of x. 2F_x stretches 2x.

• In the absence of friction, mass will continue to oscillate

Which is not an example of approximate
simple harmonic motion?

a. A ball bouncing on the floor.
b. A child swinging on a swing.
c. A piano string that has been struck.
d. A car's radio antenna as it waves back and forth.

a. A ball bouncing on the floor

• bounce is nonlinear: hits floor, stops, jumps

• Force is NOT proportional to displacement

Uniform Circular Motion (UCM)

• speed is constant but velocity is not (direction keeps changing)

• centripetal acceleration a_c always pulls toward center

• constant speed → no work done by centripetal force

  • but torques can change rotational KE: W = torque * theta

SHM vs. UCM

• SHM = edge view

• UCM = top view

Position of an object in SHM

• x(t) = Acos(ωt)

  • ω: angular frequency of oscillation = 2pi(f)

A block is hung vertically at the end of a spring. When the block is displaced and released, it moves in SHM. Which one of the following statements is true concerning the block?

a) The maximum acceleration of the block occurs when its velocity is zero.
b) The velocity of the block is never zero m/s.
c) If the velocity of the block is zero m/s, its acceleration is zero m/s2.
d) The maximum velocity occurs when the maximum acceleration occurs.

• velocity = 0 at top of swing when it is changing directions

• a. Maximum acceleration occurs at maximum displacement, when velocity is zero

  • maximum acceleration occurring when it is changing direction (0→100)

Mass-Spring System - SHM

the force on a mass on a spring is proportional to the displacement and acceleration

Angular Frequency of a mass-spring system in SHM

• ω² = k/m → ω = sqrt(k/m)

• describes how quickly the system oscillates around its equilibrium position

In a supermarket, you place a 22.3-N (around 5 lb) bag of oranges on a scale,
and the scale starts to oscillate at 2.7 Hz. What is the force constant (spring constant) of the spring of the scale?
A) 650 N/m
B) 600 N/m
C) 330 N/m
D) 820 N/m
E) 410 N/m

• F = 22.3 N

• w = 5 lb

• f = 2.7 Hz

• k = ?

• ω = 2pi(f) = 2pi(2.7) = 17 rad/s

• ω = sqrt(k / m)

  • find mass:

    • w = mg

    • 22.3 N = mg → m = 2.28 kg

• 17 rad/s = sqrt(k / 2.28 kg)

• k = 656.17 N/m

Conservation of Mechanical Energy in SHM

• In a mass-spring system undergoing simple harmonic motion, the total mechanical energy is conserved, with potential energy being converted to kinetic energy and vice versa, remaining constant throughout the oscillation.

• ME at all A values is equal

• As KE increases, PE decreases and vice versa

Suppose that the block has mass m = 2.72 x 105 kg and is designed to oscillate at frequency f = 10.0 Hz and with amplitude x_m = 20.0 cm. What is the total mechanical energy E of the spring-block system?

A) 2.147 x 107 J
B) 1.073 x 109 J
C) 3.103 x 107 J
D) 2.720 x 105 J

• E = U + K

• E = ½ kA²

• ω = 2pi(f) = 2pi(10 Hz) = 63 rad/s

• ω = sqrt(k/m)

• 63 = sqrt(k / 2.72×10^5)

• k = 1.07×10^9

• E = ½ (1.07×10^9)(0.2m)²

• E = 2.147×10^7 J
  

Simple Pendulum

• a point mass hung by a massless string

• apply Newton’s 2nd Law F = ma = -mgsin(theta)

If you have 2 different pendula, one with 5g mass, one with 10g mass, and the same L, what are their periods?

• T = 2π√(L/g) for both

• mass does not impact the period of the pendulum

Physical Pendulum

• solid mass of any shape oscillating around its com in a circular arc

• cannot be modeled as a point mass suspended by a massless string

At the surface of Mars, the acceleration due to gravity is 3.71 m/s2. On Earth, a pendulum that has a period of one second has a length of 0.248 m. What is the length of a pendulum on Mars that oscillates with a period of one second?

a) 0.0940 m
b) 0.143 m
c) 0.248 m
d) 0.296 m
e) 0.655 m

Earth

• g = 9.8 m/s²

• T = 1 s

• L = 0.248 m

Mars

• g = 3.71 m/s²

• T = 1 s

• L = ?

• T = 2pi√(L/g)

• 1 = 2pi√(L / 3.71m/s²)

• L = 0.094 m

Damped Oscillation

• oscillation through fluid (water, oil)

• amplitude decreases exponentially as energy is lost over time, leading to a gradual stop in motion

  • underdamping

• position as a function of time

• b in equation is dampening constant

  • depends on shape of object and density of medium

• examples: car suspension spring, bungee jumping

• compared to SHM: no friction, keeps oscillating

Damped Oscillation depends on…

• fluid’s viscosity

  • thickness, resistance to flow

• low viscosity fluid (ie water): vibrating motion = preserved

  • underdamped/light damping: amplitude of vibration decreases in time until motion ceases

• high viscosity fluid (ie syrup/oil): faster amplitude decrease

  • critically damped: object returns rapidly to equilibrium after it is released and does not oscillate

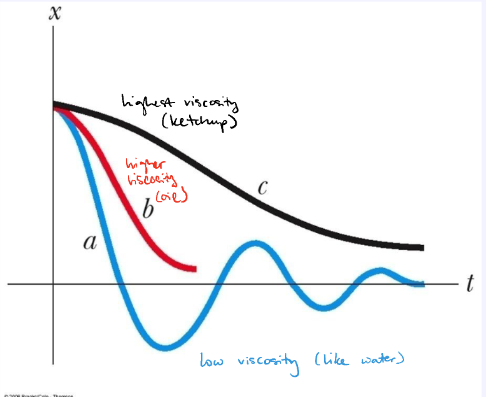
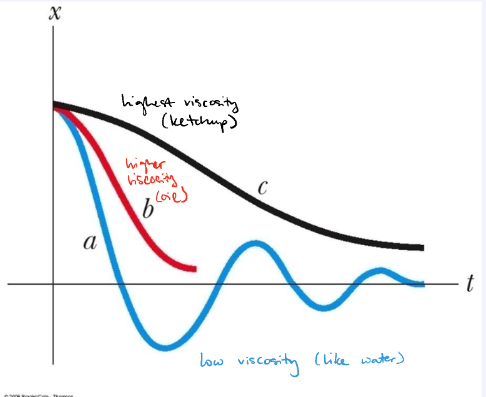
What would a car suspension spring be?

• A

  • underdamped

• B is critically damped

• C is overdamped

A particle undergoes damped harmonic motion. The spring constant is 100 N/m; the damping constant is 8.0 x 10-3 kg∙m/s, and the mass is 0.050 kg. If the particle starts at its maximum displacement, x = 1.5 m, at time t = 0, what is
the amplitude of the motion at t = 5.0 s?

A) 1.5 m
B) 1.3 m
C) 1.0 m
D) 0.67 m
E) 0.24 m

• k = 100 N/m

• b = 8.0×10^-3 kg*m/s

• m = 0.050 kg

• x_max = 1.5 m = A when t = 0

• t = 0 → 5 s

• A = ? when t = 5s

• x = Ae^(-bt/2m) cosω_dt

• A(t) = Ae^(-bt/2m)

• A(5) = 1.5e^((8.0×10^-3×5)/2×0.05kg)

• A = 1 m

When the oscillator is subjected to an external force that is periodic, the oscillator will…

• exhibit forced/driven oscillations

• example: a swing in motion is pushed with a periodic force of angular frequency, ω_d

What 2 frequences are involved in a forced driven oscillator?

1. ω: natural angular frequency of the oscillator without presence of external force

2. ω_d: angular frequency of the applied external force

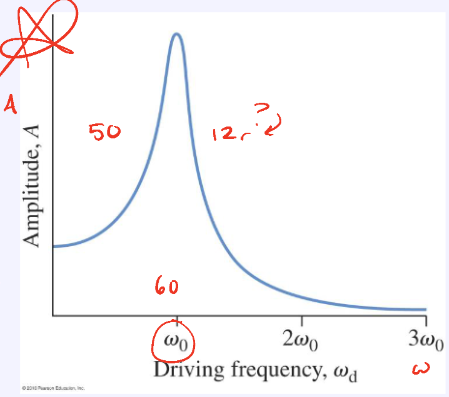
The velocity amplitude of the oscillations is greatest when…

• ω = ω_d

• this is resonance

• when displacement amplitude is largest as well

Significance of resonance

• when the frequency of an object matches with the external frequency, it starts to oscillate violently

• this results in a very high amplitude and collapse

  • ω = ω_external

  • f = f_external

For many centuries, soldiers have been trained to march side by side with their steps matching all of the other soldiers. At time t = 0 s, the soldiers all step with their left feet and continue marching with the same period. When they come upon a bridge, how should they change their marching, if at all?

a) They should continue marching with the same period.
b) Every other row of soldiers should take two steps for every one taken by the rows of soldiers ahead and behind them.
c) Every other row of soldiers should take a step with their right foot when the rows of soldiers ahead and behind them are stepping with their left feet, but keep marching with the same period.
d) They should all walk at their own pace so that they do not cause resonance on the bridge.

d) They should all walk at their own pace so that they do not cause resonance on the bridge.

• if marching frequency matches bridges natural frequency → resonance