math quiz

A rumor spreads among a population of N people at a rate proportional to the product of the number of people who have heard the rumor and the number of people who have not heard the rumor. If p denotes the number of people who have heard the rumor, which of the following differential equations could be used to model this situation with respect to time t, where k is a positive constant?

dp/dt=kp(N-p)

A rectangle has length , width , and area . The instantaneous rate of change of the area with respect to the width is equal to the sum of the length and twice the width. Which of the following equations describes this relationship?

dA/dy=x+2y

A population described by a function at time decreases at a rate proportional to . Which of the following differential equations could describe the rate of change of the population?

dP/dt=-0.015P

The height of an object at time t>1 is given by h(t)=t²-16/t+15. What is the velocity of the object at time ?

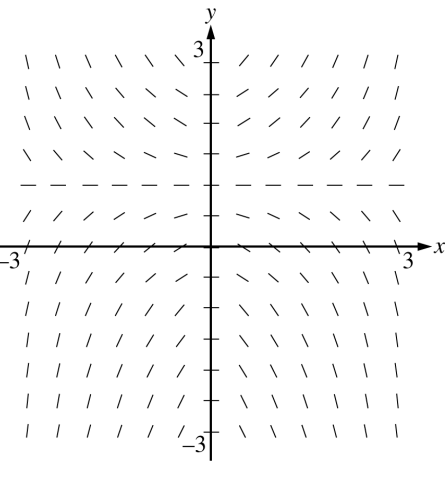
Shown above is a slope field for which of the following differential equations?

dy/dx=xy-x

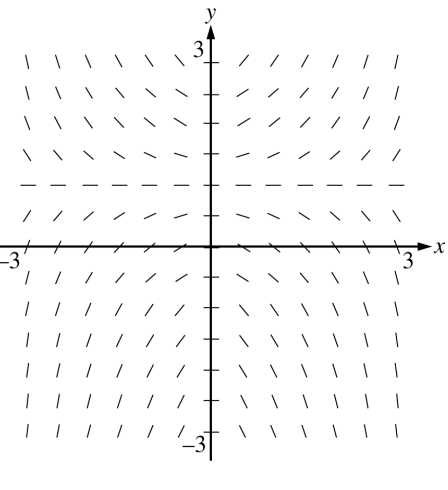
The slope field for a certain differential equation is shown above. Which of the following statements about a solution y=f(x) to the differential equation must be false?

The graph of the particular solution that satisfies f(0)=-2 is concave up on the interval -1<x<3

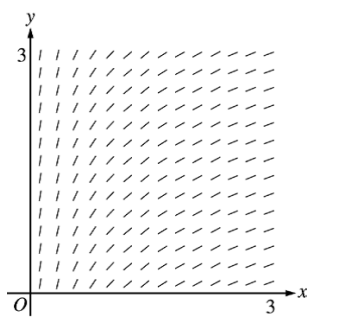
The slope field for a certain differential equation is shown above. Which of the following could be a specific solution to that differential equation?

y=ln x

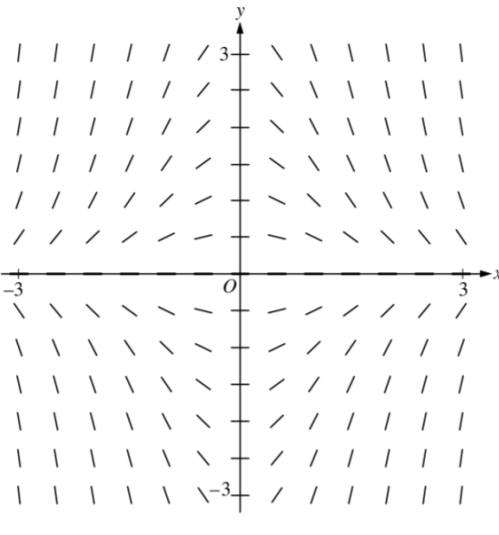
Shown is a slope field for which of the following differential equations?

dy/dx=-xy

What is the general solution to the differential equation dy/dx = (cosxe^sinx)/(cosy)

y=arcsin (e^sinx+c)

What is the general solution to the differential equation dy/dx=√y-√ysinx for y>0?

y=1/4(x+cosx+c)²

The function y=f(x) satisfies the differential equation dy/dx=2xy with the initial condition f(0)=5. What is the value of f(2)?

5e^4

The temperature of a solid at time t>=0 is modeled by the nonconstant function H and increases according to the differential equation dH/dt=2H+1, where H(t) is measured in degrees Fahrenheit and t is measured in hours. Which of the following must be true?

ln|2H+1|=2t+C

If dy/dx=16sin³xcosx and y=16 when x=π/2, what is the value of y when x=π/6?

49/4

Let y=f(x) be the particular solution to the differential equation dy/dx=y² with the initial condition f(1)=1. Which of the following gives an expression for f(x) and its domain?

f(x)=1/(2-x) for x<2

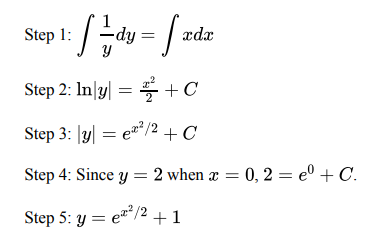
A student attempted to solve the differential equation dy/dx=xy with initial condition y=2 when x=0. In which step, if any, does an error first appear?

Step 3

If dy/dx=4y and if y=4 when x=0, then y=

4e^4x

A puppy weighs 2.0 pounds at birth and 3.5 pounds two months later. If the weight of the puppy during its first 6 months is increasing at a rate proportional to its weight, then how much will the puppy weigh when it is 3 months old?

4.6 pounds

Extreme heat applied to a colony of microorganisms causes the size P of the colony, measured in grams, to decrease according to the exponential decay model dP/dt=-0.4P, where the time is measured in hours. The size of a second colony of microorganisms, also measured in grams, decreases at the constant rate of 1 gram per hour according to the linear model dQ/dt=-1. If at time t=0 the first colony has size P(0)=2 and the second colony has size Q(0)=3, at what time will both colonies have the same size?

2.156

The population P of a city grows according to the differential equation dP/dt=kP, where k is a constant and t is measured in years. If the population of the city doubles every 12 years, what is the value of k ?

0.058