CS2050 Exam 2

Which is true of an Abstract Data Type (ADT)?

a. An ADT is defined by the set of operations that can be applied to it.

b. An ADT provides a particular data structure to allow implementation to be efficient.

c. An ADT provides a particular implementation based on efficient use of its data structure.

d. All of a, b, and c are true.

e. None of a, b, or c are true.

a. An ADT is defined by the set of operations that can be applied to it.

Which of the following is not a “Collection ADT”?

a. Bag

b. Set

c. List

d. All of these are Collection ADTs

e. None of these are Collection ADTs

d. All of these are Collection ADTs

27. For a particular implementation of a Linked List, a head pointer is maintained but no tail pointer is maintained. In order to achieve constant time for the addItem() function, where must each item be added to the list?

a. At the head of the list

b. At the tail of the list

c. Anywhere (inserting a node anywhere in the list can be done in constant time)

d. Nowhere (it is not possible to insert a node in the list in constant time)

e. There is insufficient information given to answer this question

a. At the head of the list

Which of these would be more efficient if implemented using a linked list?

a. A “bag”

b. A “set”

a. A “bag”

When deleting a node with a particular key from a singly linked list, you must find

_______________.

a. the node containing the key

b. the node before the node containing the key

c. the node after the node containing the key

d. the head node

e. the tail node

b. the node before the node containing the key

Consider a singly linked list which is ordered by key (in ascending order). In order to insert a node

into such a linked list, you must find _______________________.

a. the node that should be before the node to be inserted

b. the node that should be after the node to be inserted

c. any node that is less than the node to be inserted

d. the head node

e. the tail node

a. the node that should be before the node to be inserted

Given a singly linked list implementation with both a head and tail pointer, which of these

operations is the most efficient?

a. Inserting a node at the end of the list

b. Inserting a node at the beginning of the list

c. Inserting a node in the middle of the list

d. Either a or b is equally efficient

e. Any of a, b, or c is equally efficient

A

Given a singly linked list implementation with both a head and tail pointer, which of these

operations is the most efficient?

a. Deleting a node at the end of the list

b. Deleting a node at the beginning of the list

c. Deleting a node in the middle of the list

d. Either a or b is equally efficient

e. Any of a, b, or c is equally efficient

b. Deleting a node at the beginning of the list

If one were to push the integers 1,2,3 onto a stack, what order would they be removed via repeated

calls to the pop operation?

a. 1, 2, 3

b. 3, 2, 1

c. 2, 3, 1

d. 2, 1, 3

e. 3, 1, 2

b. 3, 2, 1

In “Big O” notation, how long does it take to access an element of an array of size N?

a. O(1)

b. O(N)

c. O(N²)

d. O(N³)

e. O(2^n)

a. O(1)

In “Big O” notation, how long does it take to print all of the integers in an array containing N

integers?

a. O(1)

b. O(N)

c. O(N²)

d. O(N³)

e. O(2N)

B. O(N)

If one were to enqueue integers 1,2,3 onto a queue, what order would they be removed via repeated calls to the dequeue operation?

a. 1, 2, 3

b. 3, 2, 1

c. 2, 3, 1

d. 2, 1, 3

e. 3, 1, 2

a. 1, 2, 3

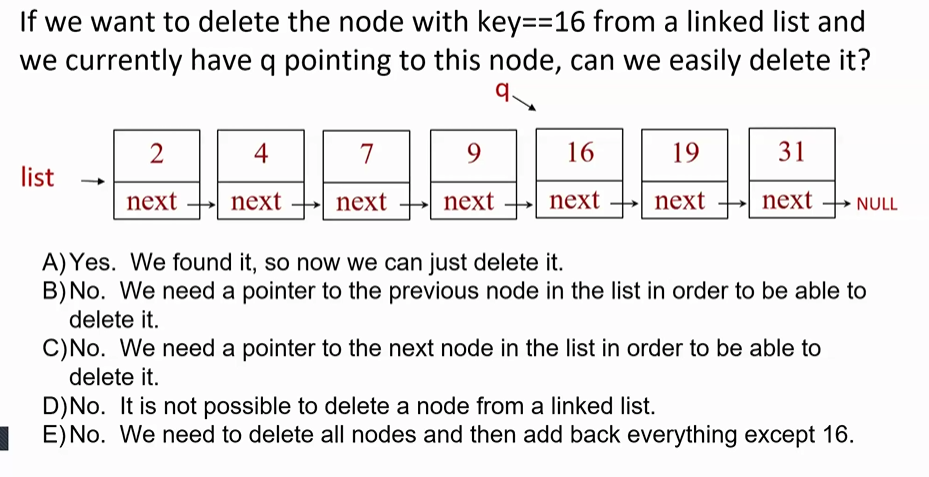
B) No - we need a pointer to the previous node in the list in order to be able to delete it

To insert a key into a linked list of sorted keys, where should q point so that we can insert a key?

We want q to point to the Node before with key smaller than the one were inserting, so the insertion occurs after that node

Suppose we want to be able to insert efficiently at either the head or tail of a list. Why is one operation more efficient than the other?

Inserting at the head takes a constant/fixed amount of time

Inserting at the tail takes time proportional to the length

How long does it take to access an element of an array of size N (ex: an array with N elements)

O(1) - constant amount of time independent of the size of the array

How long does it take to print all of the ints in an array with N integers?

O(N) - It would take time proportional to the size of the array

How long does it take to access the kth node in a linked list of length N?

O(K) - We have to traverse each node until we find k, so time is proportional to k

If one were to implement a queue as a singly-linked list with a single head pointer, how would enqueue() and dequeue() perform?

One of these functions could be O(1), but the other would have to be at least O(N)

How does a circular linked list work for a queue?

a pointer to “rear” provides O(1) access to the rear, and “rear→next” gives O(1) access to the front

What would be an incorrect first step to insert a node into a circularly linked list?

inserting at the rear will segfault if rear is NULL (unless there’s a dummy node)

5) Knowing the computational complexity of an algorithm may not provide much information about how fast it will run in practice

Two algorithms with the same complexity will perform identically on sufficiently large problems

False: big O only shows how runtime grows relative to N

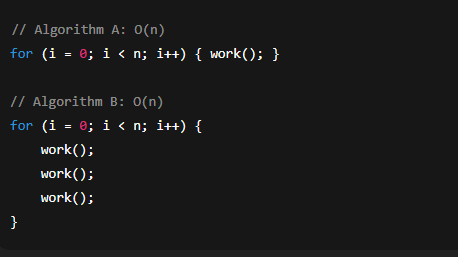
What is the computational complexity of each algorithm?

A) Algorithm A: O(1)  Algorithm B: O(1)
B) Algorithm A: O(n)  Algorithm B: O(3n)
C) Algorithm A: O(n)  Algorithm B: O(n)
D) Algorithm A: O(n²)  Algorithm B: O(n)

C: Algorithm A: O(N) Algorithm B: O(N)

Suppose someone asks about the complexity of reading a character string from a file. What is an appropriate answer?

O(N), where N is the number of characters in the string

Suppose someone asks about the complexity of reading the first 60 integers from a file containing N integers. What is an appropriate answer?

O(1) - reading only 60 integers is independent of N

Suppose a program reads M integers from file A, and N integers from file B, and then compute the sum of all the ints from the two files. What is the overall complexity to read the files and compute that sum?

O(M+N) - when choosing a big O notation, choose the best possible way to do it, and the worst case for the data

Suppose you are given a number N. What is the best complexity possible for determining if N is greater than some other given number M?

O(1) - comparing M and N is independent of what the values of M and N are

Suppose you are required to read N lines of data from a file, and each line of data contains 72 alphabetic letters. What is the complexity to print all permutations (possible orderings) of the 72 letters in each line?

O(N) - Because 72 is a fixed constant, time is relative to number of N lines of data

ex: doubling N would double the running time

Binary search assumes that the data values are stored in an ordered array

A: true

B: false

A: true

What Big O notation does Binary search take, and why?

Answer: O(log N)

explanation: it repeatedly divides the search range in half

Suppose someone says that they have a search algorithm with O(1), what can be concluded?

a search algorithm will never have O(1) complexity

How can two algorithms be compared, and one be “better” than the other

Answer: Whichever has the better “worst case” scenario

Answer: O(1) - running time is independent of length of the array

O(N) - it is doing an O(1) operation O(N) times, which means time is relative to N

O(N)

it could be O(3n/2), but Big O doesnt care about constants

O(N²) - as N grows, the 2 O(N) parts grow irrelevant to O(N²)

Time required to access an element of an array?

O(1)

Time required to perform a binary search on a sorted array of size N

O(log(N))

Time required to perform a scan over a list of size N

O(N)

The time required by the most efficient sorting algorithms to sort N elements

O(N * log(N))

imagine unsorted data that I need to find an element in, should I 

A: sort it and use binary search

B: dont sort and use sequential search

B: If only accessing the data one time, just use sequential search

Why does an NxN array have O(N^4) complexity?

the entire thing scales by N

Time required to compare every element of a set N with every other element

O(N²)

Time required to list all subsets of a set of size N

O(2^n)

Time required to enumerate all permutations of N distinct symbols

O(N!)

Suppose you are told that you will be reading a data file with M lines and P integers per line, and the values of M and P will be provided at the beginning of the data file

What is the computational complexity required to input the data?

O(M*P), it scales as M and P, which could scale differently

What is the complexity required to determine the largest key in an array that is in sorted ascending order?

O(1) - The largest element would be the last element in the array

What is the complexity required to determine whether an array is sorted in ascending order?

O(N) - it would have to check every element in the array, which scales with N

What is the complexity required to determine whether an array is sorted in either ascending or descending order?

O(1) - just compare the first and last elements of the array

Complexity for N datasets, each contains 1000 integers, and returns the sum of all the integers?

O(N) - The computation depends on the size of N